Модель функционирования программной системы на основе GERT-сети

Введение. Конкуренция на рынке производителей программного обеспечения (ПО) сейчас высока, как никогда. Сокращение сроков разработки ПО, необходимость адаптации программ под различные устройства, необходимость учета программной совместимости и повышенные требования к информационной безопасности – вот неполный перечень причин, почему вопрос о надежности программного обеспечения стоит так остро.

Важнейшим фактором, определяющим качество современного программного продукта, является надежность его функционирования. Этой проблемой занимаются исследователи и производители ПО по всему миру. Программные сбои, приводящие к остановке производств или обслуживания клиентов, ошибки проектировщиков, приводящие к утечкам клиентских данных, – эти проблемы несут колоссальные финансовые и репутационные риски как крупным, так и малым компаниям. Одной из самых известных катастроф, вызванных ошибкой программного обеспечения, была гибель ракетоносителя Ariane 5 в 1996 году [1].

В то же время производители программного обеспечения вынуждены сокращать сроки разработки ПО, использовать унифицированные решения для обеспечения совместимости программных систем, привлекать к разработке удаленных специалистов. То есть, несмотря на высокий запрос на надежное ПО, разработчики вынуждены экономить.

Самый эффективный способ обеспечить надежность функционирования программного обеспечения – это проведение работ на этапе проектирования ПО. Выбор надежной архитектуры программ позволит избежать большинства трудностей и сократить затраты на устранение проблем надежности в будущем. Однако у современных исследователей нет единого подхода даже к определению термина «надежность программного обеспечения». Одни вкладывают в это понятие невосприимчивость к внешним воздействиям, другие – простоту и прозрачность программных решений, исключающую возможность возникновения ошибок [2].

Причин возникновения ошибок и сбоев в программных системах также великое множество: проблемы, связанные с проектированием, аппаратным обеспечением, поведением пользователей в системе, внешними воздействиями на систему. Отсюда и разнообразие подходов к обеспечению надежности. Это требует развития модельно-алгоритмического обеспечения, методов и средств выбора надёжного варианта ПО .

Модели оценки надежности программной системы. В данной работе применяется мультиверсион-ный подход к обеспечению программной избыточности [3]. Простое дублирование компонентов, как при аппаратном резервировании, недопустимо, так как в отличие от аппаратуры программные ошибки имеют внутреннюю природу и при дублировании не исчезнут. При введении программной избыточности воз- никновение сбоя в функционально эквивалентных модулях (версиях) на одних и тех же входных данных происходит в различных точках его исполнения, что снижает вероятность общей ошибки системы.

В исследовании используются модели надежности программного обеспечения, использующие для получения оценок различные источники данных. Одна из моделей – коэффициент надежности архитектуры ПО [4]:

M N j

R = ZZ P R j , (1) j =1 i =1

где M – число уровней архитектуры ПО; Nj – число компонентов на уровне j , j = 1, ..., M ; PU_ij – вероятность того, что компонент i на уровне j, i е {1, ..., Nj }, j е {1, ..., M}, будет использоваться; Rj - надежность компонента i уровня j.

Значения надежности отдельных компонентов ПО Rij могут быть получены в результате статистической обработки результатов тестирования или могут быть присвоены экспертом. В обоих случаях для расчёта надежности программной системы в целом придется использовать вероятности задействования программных компонентов, оценить которые экспертам непросто.

В рамках данного исследования предлагается метод получения количественных оценок надежности для отдельных программных компонентов и для программных комплексов. В качестве метода моделирования предложены GERT-сети [5].

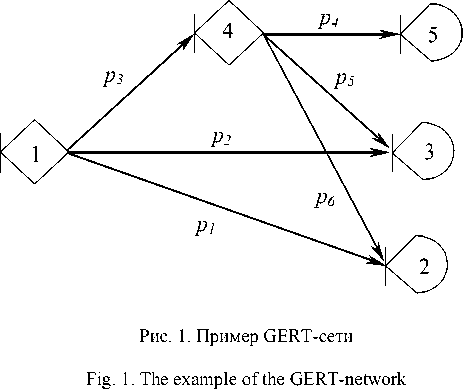
На рис. 1, где представлен пример фрагмента работы программы для ЭВМ, состояние «1» соответствует работе модуля ввода данных, состояние «2» – это следующий по очередности модуль информационной системы, переход к нему возможен с вероятностью p 1 ; состояние «3» соответствует системному сбою, который приводит к остановке работы всей программы; состояние «4» описывает работы модуля по корректировке вводимых данных, после которых возможен переход к состоянию «2», «3» или к состоянию «5», соответствующему вызову модуля по ручной корректировке вводимых данных. При этом р 1 + р 2 + р 3 = 1 и р 4 + р 5 + р 6 = 1. Состояния «1» и «4» носят вероятностный, а состояния «2», «3», «5» – детерминированный характер.

Моделирование процесса функционирования программного обеспечения GERT-сетью позволяют ответить на следующие вопросы:

• 1)    какова вероятность того, что работа программы приведет к системному сбою;

• 2)    какова вероятность того, что программа продолжит штатную работу;

• 3)    чему равны математическое ожидание и дисперсия времени, необходимого для продолжения штатной работы.

Данный подход по расчету надежности оказывается применим для оценки программных систем, состоящих из нескольких связанных исполняемых программных модулей, когда передача данных из модуля в модуль и активация следующего программного модуля происходят автоматически, без участия пользователя. Такая схема предполагает не только последовательное исполнение модулей, но и варианты с ветвлением дерева исполняемых модулей. Однако если речь идет об участии некоторого пользовательского интерфейса, где инициация того или иного программного модуля зависит от решения пользователя или наборов внешних данных, то моделирование процесса функционирования с помощью GERT-сетей в описанном режиме не представляется возможным.

Получение экспериментальных значений надежности. Для апробации рассмотренных моделей были проведены экспериментальные исследования с программным комплексом «Протокол безопасного обмена данными» (ПБОД) [6]. Логически данный комплекс состоит из пяти программных модулей и двух хранилищ данных. Каждый модуль представлен 5–8 функциональными блоками, исполняемыми последовательно. Были проведены испытания ПБОД, составлены протоколы испытаний. В результате экспериментов были получены статистические оценки надежности функционирования 14-ти функциональных блоков, входящих в различные программные модули комплекса. В табл. 1 представлены количественные значения полученных оценок. Значения коэффициентов готовности для функциональных блоков были рассчитаны по методике, предложенной в [7].

Расчет надежности функционирования программного комплекса. Требовалось получить оценки надежности функционирования как отдельных программных модулей, так и всего комплекса ПБОД в целом. Для этого процесс функционирования каждого модуля был представлен GERT-сетью. Для статистически оцененных компонентов программных модулей в алгоритме были использованы полученные функции плотностей распределения и их характеристики (табл. 1), для остальных компонентов были предложены экспертные оценки. Пример модели функционирования для программного модуля № 5 представлен на рис. 2.

Расчетное значение коэффициента надежности архитектуры ПО согласно методике, предложенной в [7], составило R 5 = 0,7589. Вычисление коэффициента надежности архитектуры ПО по формуле (1) для программного модуля № 5 дало результат R 5 = = 0,75945375. Расхождение составило E 5 = 0,00055375.

Для оставшихся программных модулей ПБОД с помощью GERT-сетей были рассчитаны значения коэффициентов готовности Ri . Расхождения с экспертным методом также составили незначительные величины. По формуле (1) был рассчитан коэффициент надежности архитектуры R всего ПБОД (табл. 2) .

Таблица 1

№ п/п	Тип распределения	M E ( s )	Математическое ожидание	Второй момент
1	Экспоненциальное	- 1 f 1 - - ) I a J	3	0,16
2	Нормальное	е$т + (1/2) - 2 ст 2	100	0
3	Константа	n	5	0
4	Экспоненциальное	— 1 [ 1 - - 1 ( a J	95	10
5	Экспоненциальное	- 1 [ 1 - - ^ ( a J	0	0

Окончание табл. 1

№ п/п	Тип распределения	M E ( s )	Математическое ожидание	Второй момент
6	Экспоненциальное	- 1 ( 1 - - V a)	0	0,1
7	Нормальное	esm + (1/2) - 2 0 2	5	0,05
8	Нормальное	esm + (1/2) s 2 0 2	1000	10
9	Нормальное	esm + (1/2) s 2 0 2	100	6
10	Нормальное	e sm + (1/2) s 2 0 2	1000	20
11	Нормальное	e sm + (1/2) s 2 0 2	45	0,5
12	Нормальное	e sm + (1/2) s 2 0 2	20	10
13	Константа	n	20	0
14	Экспоненциальное	- 1 f 1 - s V a )	5	0,15

Моменты и производящие функции моментов

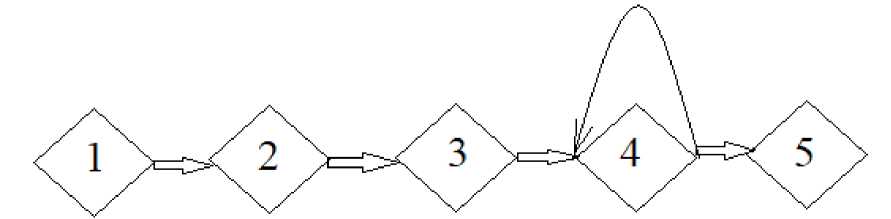
Рис. 2. Модель функционирования программного модуля № 5: 1 – блок доступа к адресной информации; 2 – блок доступа к базе входных данных; 3 – входной интерфейс блока; 4 – блок проверки формата; 5 – блок модификации программного кода

Fig. 2. The model of operation of software module № 5 (1 – Addressing information access block, 2 – Input data access block, 3 – Block input interface, 4 – Format checker block, 5 – Block of modification in the software)

Таблица 2

Результаты расчетов

Номер модуля	Коэффициентов готовности	Ошибка
R 1	0,87256001	0,00023374
R 2	0,70564758	0,00065225
R 3	0,90590065	0,00044870
R 4	0,65729975	0,00070024
R 5	0,75945375	0,00055375
ПБОД R	0,62007891

Проектирование надежного варианта программного комплекса. Для обеспечения надежности функционирования программного комплекса был использован мультиверсионный подход. В работе рассмотрено два распространенных подхода в мульти-версионном программном обеспечении: первый подход – мультиверсионное программирование (N-version Programming, NVP), второй подход – блок восстановления (Recovery Block, RВ) [8]. Был разработан многокритериальный генетический алгоритм, позволяющий определить эффективные с точки зрения надеж- ности и стоимости разработки программные блоки, подлежащие мультиверсионному дублированию, способ реализаций мультиверсий (NVP или RB), а также количество версий каждого блока.

Задача выбора надежной архитектуры сформулирована в виде задачи многокритериальной смешанной оптимизации с алгоритмически заданными целевыми функциями. Критериями задачи являются общий коэффициент готовности программного комплекса и трудоемкость, которая также зависит от количества и состава программных компонентов комплекса:

Ts =

M N j (                        (           K ij

= У У BT + N^u + RB„ У NVXH+ У Tk

^-i Z—i ij ij \ ij         ij )           ij ^i ij

j =1 i =1

k e Z i

при ограничении Zij ≥ 1, где М – количество архитектурных уровней в архитектуре ПО; Nj – количество компонентов на уровне j, j e {1, ..., M }; Kij - глубина программной избыточности компонента i на уровне j ; Z_ij – множество версий компонента i на уровне j ; Tij – трудоемкость разработки компонента i на уровне j ; T^kij – трудоемкость разработки версии k компонента i на уровне j, k e Zjj, чел. ч; NV Xij - трудоемкость разработки среды исполнения версий (приемочного теста для RB – или алгоритма голосования для NVP); Bij – бинарная переменная, принимающая значение 1 (тогда NV Pij = 0, RB ij = 0), если в программном компоненте не используется программная избыточность, иначе равна 0; NVPij – бинарная переменная, принимающая значение 1 (тогда Bij = 0, RB ij = 0), если в программном компоненте введена программная избыточность методом NV P , иначе равна 0; RB _ij – бинарная переменная, принимающая значение 1 (тогда B_ij = 0, NV Pij = 0), если в программном компоненте введена программная избыточность методом RB , иначе равна 0; Ts – общая трудоемкость реализации программной системы.

Задача решается многокритериальным генетическим алгоритмом. В исследовании были рассмотрены различные подходы к решению задач многокритериальной оптимизации [9–12]. Для решения задачи был реализован генетический алгоритм (ГА) с переменной длиной хромосом, позволяющий кодировать программные архитектуры, различающиеся по количеству и составу компонентов [4]. Алгоритм был исследован на множестве тестовых задач [13], результаты исследования позволяют говорить о высокой эффективности предложенной модификации. Длина хромосомы в ГА зависит от количества архитектурных уровней M и количества Ni компонентов на i-м уровне. При этом сами M и Ni выступают как переменные задачи. Zij в хромосоме задают количество версий компонента i на уровне j. На рис. 3 приведен пример кодирования программной архитектуры в виде бинарной хромосомы.

Для ГА с переменной длиной хромосом использовался специальный оператор процентного скрещивания.

В результате применения генетического алгоритма были получены различные варианты программных архитектур разрабатываемого комплекса, отличающиеся от исходной повышенной надежностью. При этом алгоритм предлагал реализовывать множество версий лишь для тех программных компонентов, которые были недостаточно надежны. Результаты работы алгоритма приведены в табл. 3.

Заключение. В данном исследовании был предложен новый способ оценки надежности программных систем. Способ позволяет получать оценки надежности функционирования программной системы на основе оценок надежности функционирования ее компонентов. Был разработан стохастический алгоритм многокритериальной условной оптимизации, позволяющий находить надежные варианты архитектуры ПО с учетом трудозатрат на реализацию ПО и возможностью использования различных подходов к обеспечению отказоустойчивости. Применение в генетическом алгоритме хромосом переменной длины и оператора процентного скрещивания позволило существенно сократить пространство поиска. Разработанный алгоритм был применен для проектирования программной системы с высокими требованиями к надежности. В ходе проведенных с системой экспериментов были получены статистические оценки надежности отдельных ее компонентов, составлена модель функционирования программной системы. В результате применения разработанного генетического алгоритма были предложены архитектуры программной системы, позволяющие существенно улучшить надежность ее функционирования.

Acknowledgments. This work was supported by the Ministry of Education and Science of the Russian Federation, agreement № RFMEFI57414X0126.

М=1

010 100 11011

10 000 01 011 11 000 10 100 10 001

Nl=2 N2=4 Zn=4 Bn, =нет ^№;=да RBn =да

Z2S =3 Д.^’^нет NVP2i=^eT КВ21=нет

Z42 =4

В42 =нет

NKP42=HeT

КВ42=да

Рис. 3. Пример хромосомы в генетическом алгоритме

Fig. 3. The example of chromosome in the genetic algorithm

Результаты работы генетического алгоритма

Таблица 3

№ решения	Коэффициент готовности системы	Трудозатраты на модернизацию, чел. ч
1	0,92007891	489
2	0,87100579	367
3	0,95411304	523
4	0,96486553	597
5	0,90338740	454
Исходные значения	0,62007891	351