Модель функционирования технической системы с учетом организации регламентных работ

Многие технические системы строятся по модульному принципу. Это позволяет облегчить процесс обнаружения и замены отказавших модулей. Такие модули получили название типовых элементов замены (далее – ТЭЗ). Под ТЭЗ понимается радиоэлектронный модуль одного из уровней разукрупнения радиоэлектронных и электромеханических средств [1]. Количество типов ТЭЗ, входящих в состав системы, может составлять единицы или несколько десятков единиц. Такими системами могут быть радиолокационные, приемные и передающие радиотехнические устройства и даже локальные вычислительные сети (далее – ЛВС) автоматизированных систем специального назначения (далее – АССН). Для локальных вычислительных сетей типовыми элементами замены могут быть коммутаторы, маршрутизаторы, компьютеры автоматизированных рабочих мест и серверов, а также их комплектующие (материнские платы, карты памяти, видео- и аудиокарты, накопители на жестких дисках, мониторы и др.).

С целью обеспечения требуемой надежности функционирования ЛВС комплектуются запасные инструменты и приборы (далее – ЗИП), в состав которых входят запасные ТЭЗ, используемые для замены отказавших и изношенных элементов при выполнении ремонта и технического обслуживания ЛВС. Очевидно, что необходимо определить количество ТЭЗ каждого типа, входящих в ЛВС. Такая задача, по сути, является задачей теории управления запасами [2].

Тимофеев Владимир Васильевич кандидат технических наук, доцент, Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: компьютерные технологии, надежность программного обеспечения. Автор более 140 опубликованных научных работ. SPIN-код: 61658794, AuthorID: 883597.

В теории управления запасами спрос на запасные элементы рассматривается как выход из строя (отказ) элементов резервированной системы, при этом элемент (подсистема) со своими запасными элементами рассматривается как общее резервирование с целой кратностью с ненагруженным (холодным) или нагруженным (горячим) резервом [2]. Такой подход справедлив для решения большинства практических задач теории управления запасами. Однако есть системы, состав и режим функционирования которых не позволяют свести задачу определения числа запасных элементов к задаче определения числа резервных элементов в системе с общим резервированием и целой кратностью.

К таким режимам можно отнести типовой режим функционирования технической системы в постоянной степени готовности. В процессе эксплуатации технической системы периодически проводятся регламентные работы: техническое обслуживание сети, замена неработоспособных или изношенных элементов новыми, пополнение ЗИП необходимым количеством ТЭЗ. В межрегламентный период отказавшие ТЭЗ также заменяются на новые из ЗИП.

Другим режимом, отличным от рассматриваемого в классических задачах теории управления запасами, является режим функционирования технической системы, при котором в межрегламентный период функции отказавших элементов выполняют резервные элементы. Тогда с целью поддержания высокой работоспособности в межрегламентный период система резервируется, как правило, по мажоритарной схеме. Во время регламентных работ проводится техническое обслуживание системы, неработоспособные или изношенные элементы заменяются новыми из ЗИП, который пополняется необходимым количеством ТЭЗ. Такой режим функционирования ЛВС возможен при ее функционировании в высших степенях готовности.

Для рассмотренных режимов функционирования технической системы и ее технического обслуживания невозможно непосредственно использовать результаты решения классических задач теории управления запасами. Поэтому возникает необходимость разработки математических моделей, обеспечивающих определение количества резервных ТЭЗ, адекватных этим режимам.

Математическая постановка задачи определения количества резервных ТЭЗ для типовых режимов функционирования технической системы

Постановка задачи

Модель функционирования технической системы с учетом организации ...

Дано:

N – количество типов ТЭЗ, составляющих техническую систему;

k_i – количество ТЭЗ i -го типа ( i = 1, 2, 3, …, n ), входящих в минимальный состав системы, необходимый для выполнения ее функционального назначения;

F_i ( t ) – закон (функция) распределения времени безотказной работы ТЭЗ i -го типа;

t_м . _п - время наработки системы в межрегламентный период;

P» ( t_м . _п ) — директивная вероятность безотказной работы системы за время наработки системы в межрегламентный период.

Определить:

m_i – количество ТЭЗ i -го типа, входящих в состав ЗИП системы.

Допущения, при которых будет решаться поставленная задача:

• •    если неизвестен закон распределения времени безотказной работы ТЭЗ, то принимается экспоненциальный закон распределения; параметр X закона определяется как сумма интенсивностей отказов элементов, входящих в состав ТЭЗ; интенсивность отказов элементов берется из справочников по надежности;

• •    после проведения регламентных работ система считается новой;

• •    время проведения регламентных работ при построении модели функционирования системы не учитывается, поскольку оно значительно меньше межрегламентного периода.

Сформулированная задача, по сути, является разновидностью прямой задачи теории управления запасами, в которой осуществляется поиск такого количества резервных элементов для каждой подсистемы, которое обеспечивает требуемое значение показателя надежности системы при минимальных суммарных затратах на все резервные элементы.

Исходя из формулировки задачи, для первого режима функционирования системы следует рассматривать скользящее резервирование с ненагруженным резервом, а для второго режима – мажоритарное резервирование [3]. Поэтому выражения и методы решения прямой задачи теории управления запасами, полученные, например, в [2], напрямую использовать для решения поставленной задачи не получится.

Модель функционирования и технического обслуживания системы в первом режиме

Вероятность безотказной работы совокупности ТЭЗ i -го типа за время наработки в межрегламентный период Р » ( t_м . _п ) с учетом скользящего резервирования с ненагру-женным резервом и принятых обозначений будет определяться выражением

P ( tм . п ) = 2 ^ C Е P ( tм . п ) ] ^^j f ⁽ j^L P ( tм . п ) ,                         (1)

t          t - x 1            t - X1 -.. -x, где f(1 )■ P ( t м. п ) = jf ( x 1)j f ( x 2 )... J f ( x, ) P ( t -x 1 ---x, ) dx,--dx 1; 00   0

P ( t ) = 1 - F i ( t ) - вероятность безотказной работы ТЭЗ i -го типа за время наработки t ;

f ( t ) = —- плотность распределения времени безотказной работы ТЭЗ i -го типа в момент времени t ;

C _k^j – число сочетаний из k_i по j .

Для экспоненциального закона распределения времени безотказной работы ТЭЗ i-го типа, когда Р (t) = e-At, выражение (1) примет вид

Pc (tm. „ ) = e - ^ [1 + УЯ- ^it^ e -л(1-j) ^ ].(2)

ii

• -=1

Вероятность безотказной работы всей системы за межрегламентный период nN

, =1 Pc(tM.„ ) .(3)

Для нахождения количества ТЭЗ каждого типа, которыми должен комплектоваться ЗИП системы, необходимо знать директивную вероятность безотказной работы для совокупности ТЭЗ каждого типа P c ^d ( t_M . „ ). Вероятности P c ^d ( t_M . „ ) можно найти из выражения (4), если воспользоваться утверждением, что произведение чисел, значения которых лежат в диапазоне [0,1], будет максимальным при равных значениях сомножителей:

P ( tM . „ ) = P ( tM . „ ) ^N .                                          (4)

Количество ТЭЗ i -го типа, входящих в состав системы ЗИП, m_i можно найти из неравенства

2 ” = C - [ ^P ( t m . « ) ] k i ^{- -} f ⁽ j ) ■ P ( t m . _n ) ^ Pi ( t m . „ ).                        (5)

Алгоритм определения m_i :

• 1)    m i := 0;

• 2)    вычисление P c ( t_M . „ ) по формуле (1);

• 3)    проверка неравенства (5). Если неравенство выполняется, то значение m_i и есть искомый результат, иначе m i := m i + 1 и переход на п. 2.

Таким образом можно определить массив значений числа ТЭЗ каждого типа { m ₁ , m ₂ , … , m_N }, которыми комплектуется система ЗИП.

Модель функционирования и технического обслуживания системы во втором режиме

Системы, работающие в этом режиме, обычно резервируются по мажоритарному соединению, использующему правило «2 из 3» (Рисунок 1).

По мажоритарному типу может резервироваться вся система целиком (общее резервирование) или каждый ТЭЗ (раздельное резервирование). Во втором случае, используя «умные» мажоритарные контроллеры, можно определять отказавшие ТЭЗ. Схема резервирования ТЭЗ i -го вида по мажоритарному типу показана на Рисунке 2.

При данном резервировании мажоритарные контроллеры конструктивно входят в ТЭЗ. Тогда вероятность безотказной работы резервированного соединения ТЭЗ i -го типа P c ( t )

P c,( t ) = 3 P ² ( t ) - 2 P ³ ( t ) , где P ( t ) – вероятность безотказной работы ТЭЗ i -го типа.

Вероятность безотказной работы всей системы за межрегламентный период будет определяться выражением (3).

В рассматриваемом режиме функционирования системы обнаружение отказавших ТЭЗ и их замена на новые осуществляется не в межрегламентный период, а во время проведения регламентных работ. В любом случае для этого необходим ЗИП, содержащий достаточное количество ТЭЗ каждого типа.

Модель функционирования технической системы с учетом организации ...

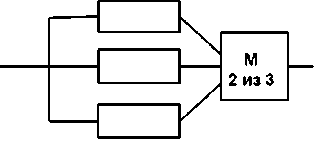
Рисунок 1. Мажоритарное резервирование

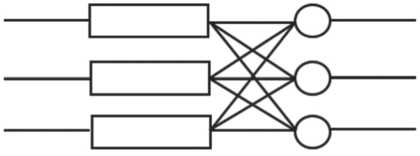
Рисунок 2. Схема резервирования ТЭЗ i-го типа

Для нахождения количества ТЭЗ каждого типа, которыми должен комплектоваться ЗИП системы m_i , необходимо рассмотреть возможный поток их отказов. Такой поток будет иметь максимальное число отказов, равное количеству модулей i -го типа с учетом их резервирования по мажоритарной схеме K i = 3 k i . Данный поток относится к редеющим ординарным потокам случайных событий (Рисунок 3). Поток отказов редеющий, так как восстановление отказавших ТЭЗ в межрегламентный период не предусмотрено, и ординарный, потому что вероятность одновременного отказа двух и более ТЭЗ намного меньше вероятности отказа одного.

Рисунок 3. Редеющий поток отказов

Функция распределения F t ( t ) моментов появления отказов в таком потоке K i ( t ) определяется следующим выражением

K - '              F t j ⁺

F t, ( t ) = l C K ^НУ С к, - j -^T- •                         (6)

j=0                  j где C mn - число сочетаний из n по m ; F(t) - функция распределения времени безотказной работы ТЭЗ.

Вероятность появления за межрегламентный период ровно r отказов ТЭЗ i -го типа P [ K i ( t_м . _n ) = r ] определяется через функции распределения моментов их появлений как

• ¹    - ^Ft 1 ( tм . n ) при ^r = 0,

^P [ K i ⁽ tм . n ) = r ] = ^Ft _r ( tм . n ) ^{- F}t _{r + 1} ( tм . n ) ^пР^{и 0}<  ^r<  K i ,                             ⁽⁷⁾

^Ft _Ki ( tм . n ) ^пР^{и r} = K i •

Вычислив вероятности P[ Kl (tм.„ ) = r] для всех значений r, получим ряд распределения числа отказов ТЭЗ i-го типа на межрегламентном периоде. Имея ряд распределения числа отказов, можно найти среднее число отказов ТЭЗ i-го типа на межрегламентном периоде mi K ш, = M[ Ki (tм.„ )] = Jr P[ Ki (tM.„ ) = r], (8) r=0

значения m_i округляются до большего целого числа.

Пример расчета количества запасных ТЭЗ для первого режима функционирования системы

Пусть количество ТЭЗ i -го типа k_i = 3, время безотказной работы имеет экспоненциальное распределение с параметром λ _i = 10 ^{- 4} , количество типов ТЭЗ в системе N = 5, директивная вероятность безотказной работы системы за время наработки в межрегламентный период P® ( t_M . „ ) = 0,9. Определить количество запасных ТЭЗ для времени наработки в межрегламентный период t_м . „ = 700 часов и t_м . „ = 1400 часов.

В Таблице 1 приведены значения вероятности безотказной работы совокупности ТЭЗ i -го типа за время наработки в межрегламентный период P ^ ( t_м . „ ), вычисленные по формуле (2), для различных значений резервных ТЭЗ ш , и t_м . „ (700 часов и 1400 часов).

Таблица 1

t М„	mi = 0	mi = 1	mi = 2
700	0,81	0,98	0,986
1400	0,66	0,94	0,99

Определим директивную вероятность безотказной работы для совокупности ТЭЗ каждого типа P® ( t_м.„ ) из формулы (4):

• i 1

P ( t«.„ ) = 0,9 5 = 0,98.

Из Таблицы видно, что для наработки в межрегламентный период t_м.„ = 700 часов, учитывая неравенство (5), достаточно иметь всего один резервный ТЭЗ i -го типа, а для tм.„ = 1400 часов - два резервных ТЭЗ i -го типа.

По аналогии с рассмотренным примером можно определить количества резервных ТЭЗ для остальных типов ТЭЗ, входящих в систему.

Пример расчета количества запасных ТЭЗ для второго режима функционирования системы

Пусть также количество ТЭЗ i -го типа k_i = 3, время безотказной работы ТЭЗ имеет экспоненциальное распределение с параметром λ _i = 10 ^{- 4} , каждый ТЭЗ зарезервирован по мажоритарной схеме «2 из 3». Определим количество запасных ТЭЗ для времени наработки в межрегламентный период t_м.„ = 700 часов и t_м.„ = 1400 часов.

Общее число ТЭЗ i -го типа с учетом резервных K_i = 3 k_i = 9. Для экспоненциального - λ t .

распределения в формуле (6) F(t) = 1 – e

Модель функционирования технической системы с учетом организации ...

В Таблице 2 приведены значения функции распределения F t ( t ) моментов появления отказов, вычисленных по формуле (6), а в Таблице 3 значения вероятностей появления за межрегламентный период ровно r отказов ТЭЗ i -го типа P [ K i ( t_м._п ) = r ], вычисленные по формуле (7), для различных значений t_м._п (700 часов и 1400 часов).

Таблица 2

^ м.п	F t 1 ( t )	F t 2 ( t )	F t 3 ( t )	F t , ( t )	F t 5 ( t )	F t 6 ( t )	F t 7 ( t )	F t 8 ( t )	Ft 9 ( t )
700	0,48	0,13	0,02	0,00	0,00	0,00	0,00	0,00	0,00
1400	0,71	0,33	0,10	0,00	0,00	0,00	0,00	0,00	0,00

Таблица 3

t мт	r = 0	r = 1	r = 2	r = 3	r = 4	r = 5	r = 6	r = 7	r = 8	r = 9
700	0,52	0,35	0,11	0,02	0,00	0,00	0,00	0,00	0,00	0,00
1400	0,29	0,38	0,23	0,10	0,00	0,00	0,00	0,00	0,00	0,00

Из Таблицы 3 по формуле (8) можно определить количество ТЭЗ i -го типа, которое необходимо иметь в составе системы ЗИП. Для наработки в межрегламентный период t_м. п = 700 часов m i = 1, а для t_{м п} = 1400 часов m i = 2.

Заключение

В условиях реальной эксплуатации технических систем неизбежно приходится восстанавливать их работоспособность из-за отказов составных частей. Очевидно, что необходимое количество запасных ТЭЗ зависит от структуры и режимов функционирования технической системы, отличающихся порядком их использования. Поэтому необходимо уметь определять количество запасных ТЭЗ для типовых структур и режимов функционирования ЛВС. Показано, что задача определения необходимого количества запасных ТЭЗ для технических систем, работающих в типовых режимах, не может быть сведена к классическим задачам теории управления запасами, поэтому разработка математических моделей, позволяющих определить необходимое количество ТЭЗ в типовых режимах функционирования технической системы, является актуальной задачей.

Приведены математические модели функционирования технической системы с учетом организации регламентных работ, а также примеры решения практических задач определения количества ТЭЗ, входящих в состав ЗИП технической системы.

Теоретическая ценность полученных результатов обусловлена тем, что разработанные математические модели определения необходимого количества запасных ТЭЗ расширяют область применения классических задач теории управления запасами и могут применяться для большого круга технических систем.

Практическая ценность полученных результатов заключается в том, что они обеспечивают возможность обоснования состава и количества ЗИП широкого класса технических систем с учетом режимов их функционирования и принятых подходов к их техническому обслуживанию.