Модель гетерогенного вычислительного процесса с глобальным распределением нагрузки на основе частных множеств

Современные тенденции возрастания скорости обработки информации в реальном масштабе времени, внедрения полностью автономных систем с искусственным интеллектом порождают соответствующие требования к производительности, масштабируемости и энергоэффективности вычислительных средств в составе военной и специальной техники [2]. Гомогенные системы, которые до недавнего времени составляли основу парка мобильных вычислительных систем и бортовых вычислительных комплексов, в силу своей однородности имеют пределы эффективности и гибкости вычислений и, как следствие, не в состоянии в полной мере обеспечить оперативное выполнение большого объема сложных вычислений. Этот недостаток ставит разработчиков информационно-вычислительных средств специального назначения перед необходимостью поиска новых подходов.

Модель гетерогенного вычислительного процесса с глобальным распределением нагрузки ...

Шульгин Альберт Николаевич кандидат технических наук, преподаватель Военно-космической академии имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: информационновычислительные системы и технологии. Автор 30 опубликованных научных работ.

Одним из путей решения этой проблемы является использование гетерогенных вычислительных систем.

До недавнего времени в качестве основного признака неоднородности гетерогенных вычислительных систем рассматривались архитектурные различия их вычислительных компонентов. Традиционно в фокусе внимания находилось сочетание процессоров общего назначения и специализированных вычислительных модулей, например, сигнальных, графических процессоров и др. [12]. Однако многопроцессорные системы данного типа в настоящее время активно развиваются. Появляются новые решения, определяющие гетерогенность не только по архитектурному признаку, но и по функциональному [6]. В контексте вышесказанного интерес вызывают гетерогенные системы, в основе которых лежит неоднородность вычислительной мощности составляющих их информационно-вычислительных блоков (ИВБ), а также способы эффективного управления вычислительной нагрузкой.

Глобальное управление нагрузкой как основа эффективных гетерогенных вычислений

В настоящей работе рассмотрен тип гетерогенной вычислительной системы, топология которой представляет собой совокупность архитектурно идентичных, но различных по производительности ИВБ. Такое решение нашло свое воплощение в технологии ARMBigLittle [4]. В данном случае интерес вызывает управление вычислительной нагрузкой, основанное на глобальном распределении задач. В отличие от кластерной организации и принципа переключений внутри ИВБ такое решение обладает большей гибкостью и возможностью эффективного задействования вычислительного потенциала всех ИБВ [11; 13].

Структурно такая гетерогенная вычислительная среда содержит ИВБ малой мощности α1, α2, …, αg и ИВБ большой мощности β1, β2, …, βh, вычислительная нагрузка каждого из которых непосредственно управляется планировщиком ОС (рис. 1).

Основным свойством рассматриваемого типа гетерогенной системы является то, что на высокопроизводительных ИВБ задачи выполняются быстрее, чем на ИВБ малой вычислительной мощности, при этом длительность вычислений пропорциональна производительности соответствующих вычислительных блоков. Это свойство необходимо учитывать при решении задачи повышения оперативности сложных неоднородных вычислений. В данном случае для расчета и оценивания вычислительного эффекта может быть ис-

Практика программирования пользован показатель (коэффициент) неоднородности φ гетерогенной вычислительной среды, представляющий собой соотношение производительности ИВБ малой и большой мощности:

V_a ф = —,

VP где Vα– производительность ИВБ малой мощности; Vβ– производительность ИВБ большой мощности.

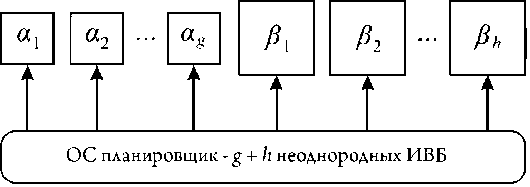
Рис. 1. Гетерогенная мультипроцессорная вычислительная среда с глобальным распределением задач

Формализация гетерогенного вычислительного процесса с глобальным распределением нагрузки на основе частных множеств

Главной характеристикой любого вычислительного процесса, реализующего тот или иной алгоритм, является время его выполнения T _алг. На временной диаграмме (рис. 2) видно, что T _алг представляет собой совокупность n распараллеливаемых участков L _пр и m последовательных (нераспараллеливаемых) участков L _пс. Следует заметить, что каждый участок L _пр, в свою очередь, состоит из параллельных частей l _пр различной вычислительной сложности и, как следствие, различной длительности выполнения.

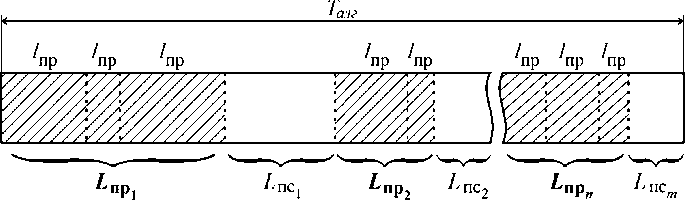
Рис. 2 . Временная диаграмма алгоритма с неоднородными параллельными участками

Декомпозиция участков L _пр на множество вычислительных модулей позволяет реализовать их параллельное выполнение, обеспечивая тем самым ускорение вычислений [3; 8] на каждом таком участке. Однако в данном случае имеет место неравномерная загрузка ИВБ, а сам распараллеленный участок L _програничивается наиболее продолжительной его частью.

На рисунке 3 видно, что участок L_np !ыполняемый на ИВБ а 1 , а 2 и а 3 определяется его частью l _пр1, имеющей максимальную длительность из всего множества параллельных частей:

^Л = ^{ l «P i ^, l »P 2 ^, l »P з ^{} .}

Модель гетерогенного вычислительного процесса с глобальным распределением нагрузки ...

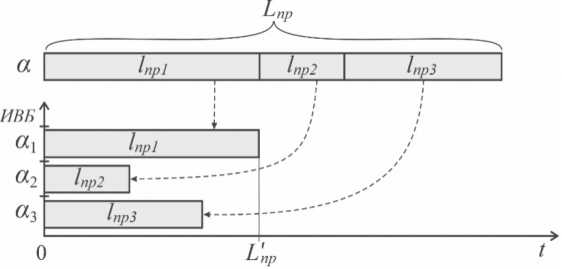
Рис. 3. Параллельный участок алгоритма с неравномерной загрузкой ИВБ

Приведенный выше пример показывает, что в гомогенных вычислительных средах к основному эффекту замедления, обусловленному наличием последовательных частей алгоритма, добавляется наличие параллельных участков большой длительности [1].

В гетерогенной вычислительной среде этот тормозящий фактор может быть преодолен за счет распределения вычислительной нагрузки между ИВБ различной производительности [5; 7]. В данном случае, если основную нагрузку возложить на ИВБ малой вычислительной мощности α, а выполнение последовательных L _пс и параллельных частей l _пр большой длительности – на β-вычислители, то это позволит получить дополнительный эффект ускорения вычислений как на локальном уровне, так и в масштабе всего алгоритма. Такую организацию вычислений можно реализовать на основе метода формирования частных множеств длительностей задач для планирования их выполнения на соответствующие ИВБ. Далее рассмотрим суть этого метода.

Наличие в параллельном участке L _пр нескольких задач большой длительности (рис. 4, а ) делает необходимым формирование множества для планирования их выполнения на β-вычислители. Однако в этом случае из соображения обеспечения энергоэффективности возникает необходимость определения оптимальных значений длительности соответствующих частей алгоритма и принятия решения планировщиком оцелесообразности их обработки на мощных вычислителях. В качестве основного критерия решения этой задачи можно использовать директивное значение l ^d, относительно которого с учетом неоднородности вычислительной системы может быть принято рациональное решение о формировании соответствующего частного множества (рис. 4, б ). Тогда частное множество Λ^α задач для α-вычислителей и, соответственно, Λ^β – для β-вычислителей определяется следующим образом:

Л ={/„р еЛ|1„р-ф< 1“}

К            ,                 (2)

где ^{Л    { 1}„P 1 , ^- 2

[Л» ={ 1„р еЛ11„р-ф> 1“}

,..., 1пр } - множество длительностей параллельных частей отдельного участка Lпр; φ – коэффициент неоднородности гетерогенной вычислительной среды (1); ld – директивное значение длительности параллельной части участка Lпр.

На рисунке 4, б показан принцип вышеизложенного подхода. Здесь задачи, длительности которых обеспечивают выполнение условия l _пр≥ l ^d, идут на формирование частного множества Λ^β, в противном случае формируется множество Λ^α. В результате имеют место две группы задач для параллельного выполнения ИВБ различной производительности.

Практика программирования

На основе (2) можно определить предельную длительность каждой параллельной группы, выбрав аргумент с максимальным значением из соответствующего частного множества:

L a = max ^л “ ; L a = ^{max л e} .

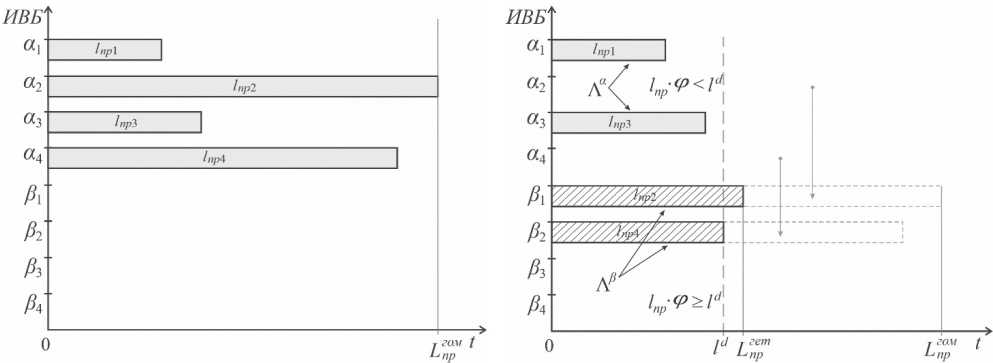
Рис. 4. Параллельный участок алгоритма:

а– с множеством частей большой длительности в гомогенной вычислительной системе;

б – в гетерогенной вычислительной системе с распределением нагрузки на ИВБ различного типа

Очевидно, что при определении величины i -го параллельного участка L _пр алгоритма определяющим будет значение L ^β_пр. В случае, если частное множество Λ^β пустое, то L _прбудет ограничен значением L ^α_пр:

K> приЛ^-О

^Mpl L^p • ф, при Л^ ^ О

Исходя из вышеизложенного длительность Tалг выполнения алгоритма в гетерогенной вычислительной среде можно определить как n        m

T„. =Z L«p.+L L-Л, i=1            j=1

где L _пр – длительность распараллеленных участков алгоритма; L _пс – длительность последовательных участков; φ – коэффициент неоднородности гетерогенной вычислительной среды (1); n – количество распараллеленных участков алгоритма; m – количество последовательных участков алгоритма.

Оценивание вычислительного эффекта в гетерогенной вычислительной системе с глобаотным распределением нагрузки

Одним из показателей эффективности параллельных вычислений является ускорение выполнения алгоритма. Закономерность роста ускорения при распараллеливании вычислений сформулирована в [9]. Однако данная закономерность предполагает изначальную фиксированность рабочей нагрузки, реализация которой рассматривалась применительно к ИВБ одинакового типа и вычислительной мощности [10].

В контексте данной работы для адекватной оценки ускорения вычислений необходимо учитывать организацию вычислений сложных алгоритмов и гетерогенность вычислительной среды.

Модель гетерогенного вычислительного процесса с глобальным распределением нагрузки ...

В данном случае, если в качестве основного принципа организации вычислений рассматривать выполнение на ИВБ большой мощности всех последовательных операций алгоритма и параллельных операций значительной длительности (определяемому по принципу, изложенному выше), ускорение вычислений S _гет алгоритма применительно к гетерогенной параллельной вычислительной среде будет выглядеть следующим образом:

s гет

(т„с + T„p )Ф +

1 - (Т„с + Т„р )• Ф к

где τ _пс – доля последовательных участковалгоритма; τ _пр– доля параллельных участков большой длительности; k – количество ИВБ основной параллельной обработки; φ – коэффициент неоднородности гетерогенной вычислительной среды (1).

Для проверки состоятельности изложенного в данной работе принципа распределения вычислительной нагрузки были проведены расчеты (3) и сравнительный анализ значений производительности для гомогенной и гетерогенной организации параллельных вычислений при различном уровне параллелизма. Результаты расчетов ускорения для гомогенной и гетерогенной вычислительной среды представлены в таблице 1.

Таблица 1

Ускорение вычислительного процесса для гомогенной и гетерогенной вычислительной среды при q = 0,5

	k = 1	k = 2	k = 3	k = 4	k = 5	k = 6	k = 7	k = 8
S	1,00	1,33	1,52	1,60	1,66	1,72	1,75	1,78
S	1,00	1,60	2,01	2,29	2,50	2,66	2,81	2,92

На рисунке 5 показаны графики зависимостей ускорения вычислительного процесса в гомогенной и гетерогенной вычислительной среде.Очевидно, что предложенный подход позволяет существенно поднять верхнюю границу ограничения на рост производительности при распараллеливании вычислений.

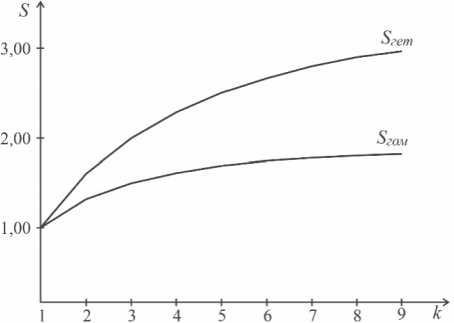
Рис. 5. Ускорения вычислительного процесса в гомогенной S _ГОм и гетерогенной S _гет вычислительной среде при q = 0,5

Практика программирования

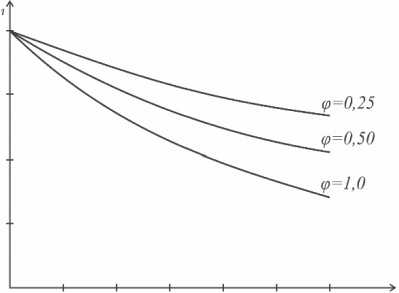
В результате исследования выявлена зависимость эффективности вычислений от изменений соотношения вычислительной мощности ИВБ гетерогенной вычислительной среды при фиксированном общем количестве вычислителей. Результаты расчетов представлены в таблице 2.

Таблица 2

Ускорение вычислительного процесса в гетерогенной вычислительной среде при фиксированном количестве ИВБ ( k = 4) и различных значениях φ

	q = T- + T „«
	q = 0,1	q = 0,2	q = 0,3	q = 0,4	q = 0,5	q = 0,6
S φ=1,0	3,07	2,50	2,11	1,82	1,61	1,43
S φ=0,5	3,48	3,07	2,76	2,50	2,28	2,10
φ=0,25	3,73	3,48	3,33	3,07	2,94	2,77

На рисунке 6 показаны графики ускорения вычислений при различных значениях коэффициента неоднородности в условиях ограниченной масштабируемости.

4,00

3,00

2,00

1,00

О OJO 0,20 0,30 0,40 0,50 0,60 7

Рис. 6. Соотношение зависимостей S от q при различных значениях коэффициента неоднородности в гетерогенной вычислительной среде

Очевидно, что при увеличении совокупной доли последовательных участков реализуемого алгоритма и параллельных частей большой длительности прирост ускорения вычислений зависит от неоднородности гетерогенной вычислительной среды и может быть получен за счетувеличения разницы в вычислительной мощности ИВБ.

Выводы

Представленная модель реализации алгоритма позволяет осуществить расчет длительности его выполнения и оценить оперативность вычислений различной сложности в гетерогенной вычислительной среде.

Принцип распределения вычислительной нагрузки в гетерогенной вычислительной системе с глобальным распределением задач, изложенный в данной работе, дает возможность:

Модель гетерогенного вычислительного процесса с глобальным распределением нагрузки ...

– получить дополнительный эффект ускорения параллельного вычислительного процесса при наличии значительной доли последовательных участков и параллельных частей большой длительности;

– выбрать оптимальную топологию гетерогенной вычислительной среды для обеспечения высокой эффективности вычислений в соответствии с объемом и сложностью задач в условиях ограничений на масштабируемость и энергоемкость функционирования.