Модель графика поставки дорожно-строительных материалов при строительстве лесовозных автомобильных дорог

Отличительной особенностью практически всех дорожно-строительных работ является их протяженность во времени. Это предъявляет особые требования к эндогенным и экзогенным переменным математической модели, а также параметрам, величина которых переменна во времени.

Суммарные затраты в дорожно-строительные материалы, поступающие на строительный объект (дорогу), формируются в результате взаимодействия внешних и внутренних технико-экономических факторов [2].

К внешним факторам можно условно отнести стоимость строительных материалов, полуфабрикатов, энергоресурсов, эксплуатации автотранспорта и дорожно-строительных машин, которая носит вероятностный характер и имеет тенденцию роста в течение года. К внутренним факторам можно внести последовательность и интенсивность потребления производственных ресурсов, которая неустойчива во времени и претерпевает сезонные изменения вследствие комплексного воздействия природно-климатических условий района строительства, физико-механических свойств перерабатываемых материалов, организации и технологии строительства.

Вследствие этого можно сделать заключение, что модель сводного графика поставки строительных материалов и энергоресурсов на строительный объект должна быть динамической. С другой стороны, она не должна быть слишком сложной, так как это затруднит ее применение на практике и едва ли увеличит точность (учитывая вероятностный характер используемой информации). В качестве целевой функции при оптимизации графика поставки производственных ресурсов на строительный объект следует использовать суммарные затраты на закупку и поставку материалов. Допустим, что информационная матрица, полученная в результате расчета, должна быть составлена с учетом уже имеющегося опыта в соответствующей области. Если обнаруживается «нестыковка», то следует пересмотреть используемую информацию, приблизив ее к реальным условиям.

Определение параметров линейной целевой функции (удельная стоимость материалов с учетом транспортных расходов в различные временные периоды t) следует выполнять на основе прогноза стоимости строительных материалов и транспортных услуг на период строительства C ( t ) , что увеличит точность получаемых результатов.

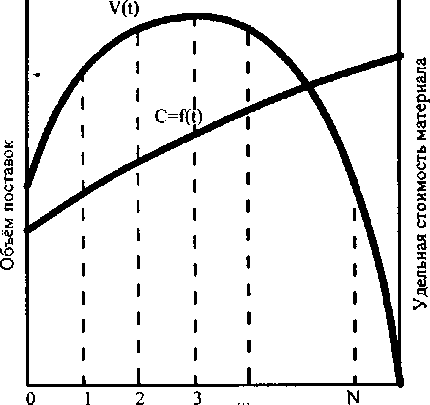
Продолжительность поставок материалов Т

Расчётная схема оптимизации сводного графика поставок ресурсов

Рассмотрим математическую модель формирования сводного графика поставки ресурсов на объект на основе графиков поставки всей номенклатуры используемых материалов (рис. 1). Обозначим Xi,j – объем поставок i-го материала в j-й период времени, i = 1,m; j = 1,n ; Wj – транспортные ограничения по периодам, определяемые провозной возможностью автотранспорта; Vi (i = 1,m) – плановые суммарные объемы поставок i-го материала; ai,j – ограничения на Xi,j – связанные с конкретными условиями поставок i-го материала в j-й период времени, определяемые условием хранения материала на строительном объекте (дороге) или производственными потребностями технологических процессов. Провозная возможность автотранспорта одинаковой грузоподъемности q за период времени ∆tj определяется по формуле [1].

W j =

∆tjAcqγcβcVτ

(Lг + tnpVTβe )(1 + Lcdn где Ac – число автомобилей, участвующих в транспортном процессе в период ∆tj ;

γ _c – коэффициент использования грузоподъёмности;

β _c – коэффициент использования пробега;

V τ – техническая скорость автомобиля, км/ч;

L_г – длина пути с грузом, км;

t_np – время на маневрирование, погрузку и разгрузку автомобиля за один цикл, ч;

L_c – среднесуточный пробег автомобиля, км;

d_n – удельный простой автомобиля в ремонте, обслуживании по организационным причинам.

Опишем систему ограничений:

∑n Xij =Vi,i=1,m j=1

a′ij ≤ Xij ≤ a′i′j,i = 1,m; j = 1,n, m∑ Xij ≤ Wj, j = 1,n.

i=1

Условие a′ij ≤ Xij ≤ a′i′j описывает достаточность поставляемого i-го материала в j-й период времени. Величина a′i,j определяется величиной страхового запаса между очередными поставками материала, a′′ определяется интенсивностью потребления i-го материала I за расчетный интервал вре-,j                                                                                         ,j мени At j, рассчитывается по формуле a i,j=a i,j + Ii,j Atj.                                  (3)

Так как интенсивность потребления ресурсов определяется производительностью ведущих машин, составом и коэффициентом их использования в составе дорожно-строительных отрядов, то ограничения a′_i,j и a′_i′_{, j} на X_i,j переменны во времени [3].

Целевой функцией при поиске оптимального решения является минимум затрат в производственные ресурсы, поставляемых на строительный объект в различные моменты времени:

^P = ^а 11^X 11 ^{+ а} 12^X 12 ^{+  + а} 1 n^X 1 n + ^a 21^X 22 ⁺ ■■■ ^{+ a} 2n^X 2 n ⁺ — ⁺

^+a m 1 ^Xm 1 ⁺ ■ ^{+ a} mn^Xmn

mn

mn

X! аЛ^Х

■ f ^а t'dX

где P i j - пределы интегрирования в j - й период времени;

fi (t) – функция общей стоимости i-го материала с учётом затрат на его закупку, транспортиров- ку и хранение.

Решение отыскивается симплекс-методом с помощью электронных таблиц MS Excell. В результате расчетов формируется двумерная матрица, состоящая из объемов поставки материалов X_i,j за дискретный интервал времени A t j (табл. 1).

Матрица решения задачи

Таблица 1

	Материалы, поставляемые на строительный объект X , 1i,j
g < 2 ф го Й з ^ S О о	X 1,1	X1,2	X 1,3		X1,m	X Х„	W 1	о  > О     1- О j о S 2 О I « 1 й S 2 Q. С    05
	X2,1	X 2,2	X 2,3		X2,m	X X 2.	W 2
	Xn,1	Xn,2	Xn,3		Xn,m	X X n,m	W j
	V n,1	V n,2	Vn,3		Vn,m	X Q	X W j

Выполнение условия возможности перевозки всех материалов за весь период времени определяется выражением Σ Q ≤ Σ W_j .

Адекватность математической модели проверяли экспериментально, использовались материалы строительной организации ООО «Крона-строй» (г. Курск) (табл. 2).

Таблица 2

Модель перевозки материалов строительной организацией ООО «Крона-строй»

	Материалы, поставляемые на строительный объект X , 1i,j				∑ Q	∑ W j
Поставка материалов на объект с шагом Δt j , 1	800	100	340	1500	2740	2950	Провозная способность автотранспорта W j
	750	120	450	1500	2820	2950
	600	110	310	1000	2020	2950
	2150	330	110	4000	7580	8850

При перевозке использовались транспортные средства: ЗИЛ – 450 усл.ед. объема перевозимого груза (провозная способность), МАЗ – 1000 усл. ед. объёма перевозимого груза, КАМАЗ – 1500 усл. ед. перевозимого груза.

Вывод. Предложенная математическая модель оптимизации сводного графика поставки дорожностроительных материалов позволяет создать предпосылки для оптимизации суммарных затрат на поставку строительных материалов и энергоносителей, основана на прогнозе изменения стоимости материалов и услуг в период проведения дорожно-строительных работ, провозной способности транспортного звена и интенсивности потребления ресурсов в период строительства лесовозных автомобильных дорог.