Модель хранилища данных для формирования управленческой отчетности в телекоммуникационной компании на платформе SAP BW

Современные вычислительные системы позволяют работать с большим объемом данных, нежели несколько лет назад. Создаваемые проекты способны анализировать числа, имеющие все больше разрядов. Соответственно, их проверка занимает гораздо больше времени и сил. Поэтому на сегодняшний день проблема автоматизации процесса тестирования становится актуальной.

Существует ряд подходов для проверки правильной работы оборудования:

• -    проверка, использующая входные данные, внесенные пользователем;

• -    исчерпывающее тестирование;

• -    перебор псевдослучайных чисел за определенный отрезок времени.

• 31...28 27...24 23...20 19...16 15...12 11...8 7...4 3...0I у Л r II у Л r II у IL^—IL—^—IL^-J

  Х8 Х7 Х6 Х5 Х4 ХЗ Х2 XI

Первый метод позволяет проверить лишь единичные наборы, которые выбраны пользователем, поэтому не может стать исчерпывающим средством для тестирования проекта. Проверка оборудования на случайных наборах дает более полный результат, однако могут возникнуть ситуации, когда на каком-то наборе проверяемое оборудование работает некорректно.

Более качественная проверка происходит при втором способе, когда производится полный перебор всех наборов используемых в работе операндов. Однако данный способ может быть использован, когда это допустимо по времени. Это значит, что при большом количестве вариантов данный метод может привести к зависанию тестирующего стенда.

Самой сложной задачей для проверки арифметико-логических устройств является задача проверки умножения. Для тестирования подобных устройств при работе с числами, находящимися в тридцати двух разрядной сетке, необходимо сформировать 4294967296 уникальных наборов, на каждом из которых произвести непосредственно проверку оборудования и вывести результаты в виде, понятному пользователю. В этом случае ориентировочное время выполнения тестирования составляет 1,8 часа, что недопустимо по времени.

Для проведения полного тестирования, используя при этом сравнительно небольшое число наборов, создан метод, работающий согласно теореме:

Пусть результат представлен числом, находящимся в 32-х разрядной сетке. Тогда при делении результата на t равных частей (X₁... X_t) (см. рисунок 1), каждая группа разрядов X i будет повторяться через X i+1 +K, где: X i+1 – разряды следующей группы результата, а K – соответственно значение множимого.

Рисунок 2 – Разделение результата на отдельные группы разрядов

Основной причиной выявленной закономерности является кодирование операндов (представление операндов в двоичном коде). Внутри каждой группы по m разрядов при переборе всех вариантов формируются наборы, равные: 0, 1, 2 … 2m – 1. При достижении крайнего числа (2m – 1) производится увеличение значения следующей группы на 1 и обнуление всех разрядов в группе.

Таким образом, в одной и той же группе производится перебор одних и тех же множителей (0, 1, 2 … 2m – 1) для каждого множимого. Следовательно, есть группы результатов, которые повторяются через каждые Р наборов множителя.

Пусть значение множимого равно N. Тогда значение результата операции в каждой группе будет равно: 1*N, 2*N … N*2k – 1, k – число разрядов в каждой группе результата. Соответственно, так как разряды результата изменяются на N, то группа повторяющихся разрядов зависит от изменения следующей группы на величину N.

Сформулированная теорема может стать основой для метода, являющегося аналогом полного перебора.

Рассмотрим простой пример.

Пусть каждый результат разделен на группы по k разрядов каждая. Тогда для множимых от 0 до 2k-1 производится полный перебор всех множителей, необходимых для проверки младшей группы Х1. Когда множимое находится в пределах от 2k до 22k-1, производится проверка следующей группы, то есть группы Х2. Аналогичным образом производится проверка и всех остальных групп.

Таким образом, метод, создаваемый на основе описанной выше теоремы, способен произвести проверку всех разрядов групп путем полного перебора всех вариантов множимых. Т.е. производится проверка, аналогичная полному перебору.

Однако, данный метод справедлив далеко не во всех случаях.

Как известно, числа могут быть представлены в прямом, обратном или дополнительном коде. При этом положительные и отрицательные числа в прямом коде отличаются лишь знаковым разрядом (у отрицательных чисел он равен единице). Следовательно, в этом случае метод, созданный на основе теоремы, выполняет полную проверку всех выходных разрядов после выполнения умножения.

Если числа представлены в обратном или дополнительном коде, как известно, положительные числа в этом случае отличаются от отрицательных. Следовательно, есть необходимость дополнительно проверять и отрицательные числа. Следует учесть, что описанная выше теорема будет справедлива для всех наборов, и, соответственно, – для отрицательных чисел.

Описанный метод справедлив не только для операций умножения, сложения или вычитания, но в силу представления чисел в двоичном коде – для логических операций. При этом зависимость, на основе которой сформулирован метод, остается прежней.

В этом случае необходимы дополнительные уточнения:

– Следует учесть, что при выполнении операции вычитания и деления значение каждой повторяющейся группы X i зависит от уменьшения значения последующей группы X_i+1 на значение N – значение второго операнда.

– В случае, когда операция зависит от дополнительных параметров, как операция сдвига от количества сдвигаемых разрядов, каждая повторяющаяся группа результатов X i зависит от изменения значения группы X_i+1 на значение Q, где Q – дополнительный параметр, например, количество сдвигаемых разрядов в случае сдвига операнда.

– В случае выполнения операции, где используется только один операнд, например, операция побитовой инверсии, каждая повторяющаяся группа результатов X i зависит от изменения значения группы X i+1 на значение 1.

Данный метод был применен для усовершенствования стенда для проверки курсовых проектов студентов в рамках дисциплины «Организация ЭВМ и систем». Тестирующий стенд был создан, как аппаратнопрограммный комплекс на основе стенда DE2-115 компании Altera. Основной особенностью АПК является то, что тестируемый проект входит в состав ядра программируемой процессорной системы, загружаемой на DE2-115. Таким образом, происходит проверка аппаратуры, входящей в состав процессорной системы.

Максимальная разрядность сетки, в которой находится результат, равна 32. Это значит, что максимальное число уникальных наборов в режиме полного перебора равно 4294967296, что является недопустимым по времени проверки каждого проекта. Поэтому для данного АПК на основе описанной теоремы был создан метод сокращенного тестирования.

Количество вариантов в этом случае указано в таблице 1.

Таблица 1 – количество наборов в зависимости от количества разрядов в группе

Метод	Способ	Количество разрядов в группе	Общее число наборов
Р0	N=2	2	3392
Р1	N=4	4	27776
Р2	N=8	8	16711680
Р3	N=16	16	3519630540800

В силу того, что необходимо проверить аппаратуру, т.е. проект, созданный, как электронная схема, можно ввести некоторые допущения:

• -    пусть будет производиться перебор множимых, как чисел: 0, 1, 2¹,2² и т.д., т.е. множимых, от которых зависят конкретные разряды результата;

• -    для проверки можно разделить результат на 32 группы, так как необходимо проверить корректность реакции каждого разряда результата.

Тогда в этом случае количество наборов будет представлено в табл. 2.

Таблица 2 – Зависимость количества уникальных наборов от количества разрядов в группе после применения допущений

Метод	Количество разрядов в группе	Количество наборов
Р0	2	1472
Р1	4	3360
Р2	8	456704
Р3	16	1610350592
Р4	1	128

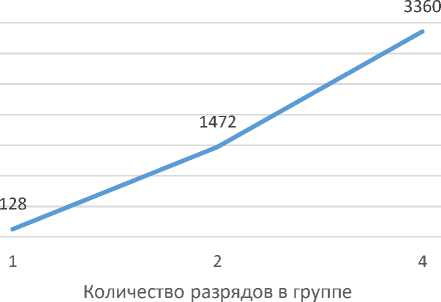
График зависимости представлен на рисунке 2.

Зависимость количества наборов от количества разрядов в группе (Р0, Р1, Р4)

□Q 3500

о 3000

VO т 2500

s 2000

I— у 1500

^ 1000

о

Рисунок 2 – График зависимости количества наборов от количества разрядов в группе для методов Р0, Р1, Р4.

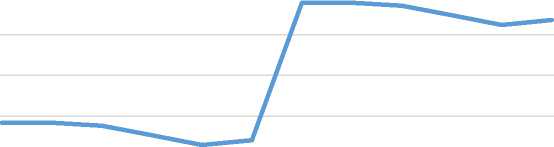
Таким образом, очевидно, что количество наборов в методе Р4 значительно меньше чем 232. Соответственно, время выполнения в начальном режиме (см. рисунок 3) будет значительно больше, чем в методе Р4 (см. рисунок 4).

Зависимость времени выполнения тестированя в режиме полного перебора от вариантов ТЗ

8000 и 7000 § 6000 го 5000 О 4000 н 3000 н 2000 1 1000

1     2     3     4     5     6     7     8     9    10    11    12

Варианты ТЗ

Рисунок 3 – График зависимости времени выполнения тестирования в режиме полного перебора от вариантов технического задания (ТЗ)

Зависимость времени тестирования от вариантов ТЗ

0,003

0,0025

0,002

0,0015

1     2     3     4     5     6     7     8     9    10    11    12

0,001

0,0005

Варианты ТЗ

Рисунок 4 – График зависимости времени выполнения тестирования в режиме сокращенного тестирования от вариантов технического задания