Модель и алгоритм трехмерной визуализации численных результатов для поддержки принятия технологических решений

В настоящее время при управлении технологическими процессами разработки месторождений полезных ископаемых методом подземного выщелачивания и принятия технологических решений геологическими службами широко используются вычерченные карты изобар по фактически измеренным данным на скважинах [1]. С помощью этих данных интерполированием и экстраполированием определяются данные и на других точках пространства.

Для облегчения анализа полученных численных результатов для поддержки принятия технологических решения, разработан алгоритм вычерчивание трехмерного графика для визуализации двумерных численных результатов. Основным трехмерном графическим примитивом в компьютерной графике на сегодняшний день является треугольник, задаваемый координатами его вершин. Как правило, для каждой вершины задаются ее положение в пространстве X,Y,Z, цвет (R,G,B) или координаты в текстуре (S,T).

Для задания неплоских гладких поверхностей используются различные методы описания поверхностей параметрическими функциями от двух параметров. Сложные поверхности собираются из отдельных кусков (patch), каждый из которых является полиномом. Такой полином можно растрировать двумя способами.

Во первых, его можно представить интерполирующим многогранником, каждая элементарная грань которого будет являться треугольником или прямоугольником. Другой подход состоит в растрировании семейства близко лежащих линий, для генерации которых можно использовать аппаратно реализованный генератор кривых. Второй подход, как правило, не применяется, поскольку простые видеокарты способны аппаратными средствами генерировать кривые Безье [2].

Наиболее употребительными кусочными функциями являются петчи Безье и петчи Кунса. Метод Безье для проектирования кривых можно обобщить для проектирования поверхностей.

Именно это выражение мы в дальнейшем будем иметь в виду, когда будем упоминать петч Безье. Следует, однако, отметить, что имеется еще один метод получения двухпараметрической функции на основе кривых Безье. Этот метод основан на использовании булевой суммы вместо декартова произведения. Но мы не будем использовать этот способ построения петча из-за его недостаточной наглядности и излишней сложности.

Проиллюстрируем геометрическое задание петча Безье на примере бикубического петча (m = n = 3). Для задания петча Безье достаточно задать набор m x n точек в пространстве. Такой набор задает полигональную сетку (рис.1).

Чтобы обеспечить гладкое сопряжение двух смежных петчей, необходимо, чтобы смежные ребра были коллинеарные. На рис.2 показано гладкое сопряжение двух бикубических петчей Безье. Для гладкого сопряжения двух петчей, как это показано на рис.2, необходимо чтобы были коллинеарные следующие тройки точек: (02,03,04), (12,13,14), (32,33,34). В этом случае при интерполяции возникнет визуальная иллюзия гладкой поверхности многогранника.

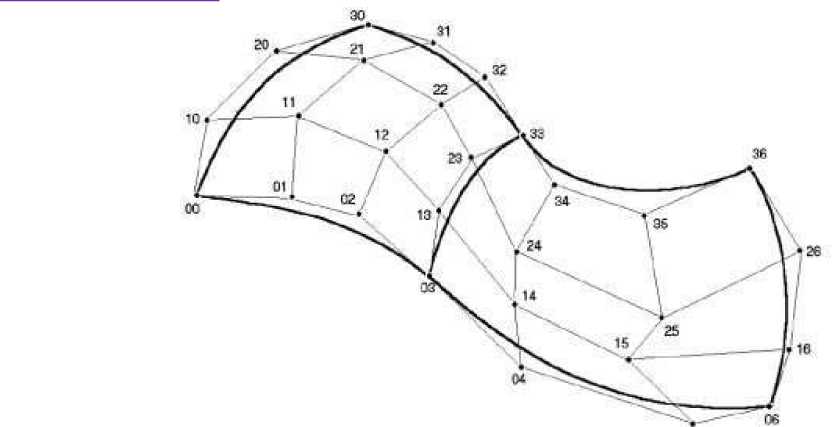
Рис.2. Гладкая сопряжения двух петчей Безье

Рассмотрено кривых и поверхностей, используемых в компьютерной графике, и во всех случаях основным параметром, определяющим форму кривой или поверхностей, был набор опорных точек – вершин управляющего многоугольника или многогранника. Для выполнения геометрических преобразований – масштабирования, смешения, поворота заданного объекта необходимо подвергнуть этим преобразованиям каждую Матричная  запись  геометрических преобразований очень  удобна, поскольку  позволяет задать геометрическое преобразование  в виде композитной матрицы, полученной перемножением матриц элементарных преобразований (масштабирования и поворота). Однако преобразование смещении Яне является матричной операцией, что не позволяет в самом общем случае получить матричное преобразование на основе матриц размерности 3х3. этот недостаток можно обойти, если задавать координаты точки однородными координатами.

Координаты точки x,y,z можно задать четверкой чисел X,Y,Z,h, где h□ 0. связь между однородными и не одно р одны м и координатами точки.

Очевидно, что четверку X,Y,Z,h, однозначно задающую положение точки, также можно считать ее координатами. Однородные координаты замечательны тем, что с их помощью можно задать все геометрические преобразование в виде матричных операций и получить, таким образом, композитное преобразование в виде одной матрицы.

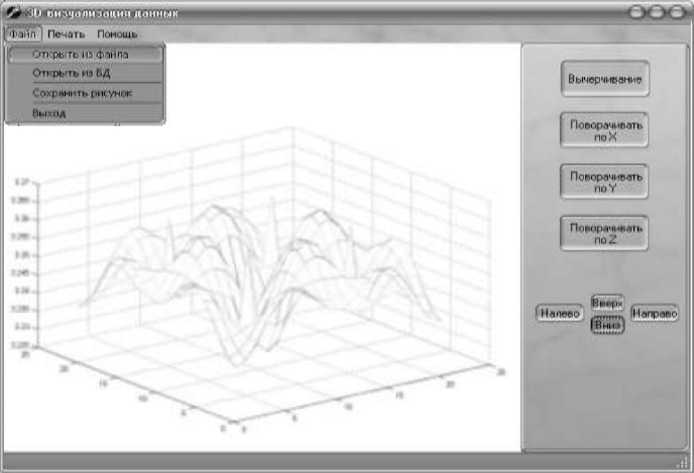
Рис.3. Окно интерфейса трехмерной визуализации

Для реализации описанного выше алгоритма построения трехмерного визуализации двумерных данных разработано программное обеспечение на языке Delphi (рис.3).