Модель импульсной характеристики декаметрового канала связи с идентификацией параметров многолучевости

В радиосистемах между передатчиком и приемником часто возникают многолучевые непрямые трассы. Такое многолучевое распространение особенно значительно в декаметровом канале связи и обусловлено неоднородным отражением от слоев ионосферы. В результате принимаемый сигнал состоит из нескольких компонентов с различными временными задержками, амплитудами, фазами и направлениями прихода.

Следовательно, для улучшения рабочих показателей систем связи декаметрового диапазона необходимо обладать информацией об условиях распространения сигнала в канале, чтобы иметь возможность адаптировать к ним алгоритмы приема с целью обеспечения оптимальной обработки сигнала. Для этого необходимо проводить зондирование канала связи, т. е. осуществлять передачу по нему некоторого заранее известного сигнала, прием и обработка которого позволяют оценить параметры канала.

Анализ последних исследований и публикаций [1–3] показал, что поскольку набор случайных и детерминированных факторов, оказывающих существенное влияние на передачу сигналов в декаметровом канале связи, разнообразен, то целесообразно при его моделировании использовать феноменологический подход, так как соответствующие структурно-физические модели из-за своей сложности малопригодны для синтеза алгоритмов приема сигналов. При этом для феноменологических моделей канал рассматривается как «черный ящик», внутренняя структура которого при описании не учитывается, а основное внимание уделяется воспроизведению взаимозависимостей между входными и выходными воздействиями.

Цель работы заключается в построении модели канала связи, которая в отличие от наиболее часто применяемых (конкретизированных) моделей позволяет представить его на основе его импульсной характеристики с использованием теории марковских случайных процессов.

Постановка задачи

Так как свойства большинства реальных сред распространения радиоволн становятся нелинейными только при очень мощных сигналах, не характерных для радиосвязи, то декаметро-вый канал можно рассматривать как линейную и узкополосную систему.

Тогда представим в фиксированный момент времени реализацию его импульсной характеристики по модулю в виде [4, 5]

^H т |⁼[h_m Т cos со 0 т-ф т J rect г^/г max = [ h_c т cos о 0 ТА-h_s Т sin G) 0^Г] rect Т / Т max ,

где h m (τ), h c (τ) и h s (τ) – огибающая и квадратурные составляющие импульсной характеристики; ω 0 – несущая частота, соответствующая декаметровому диапазону; φ(τ) – фазовый сдвиг, отражающий характер фазовых искажений в канале, обусловленных расположением областей отражения в ионосферной линии связи и доплеровским смещением частоты; τ max – максимальное время задержки сигнала или «память» канала;

rect

т max

1 при 0        max _.

0 при 0 и      max

Принимая во внимание результаты экспериментальных исследований прохождения ради-т оволн в ионосфере с учетом многолучевости и замираний [6], в [7] предложена следующая модель квадратурных составляющих hc(τ) и hs(τ):

h_cA_cch _cm_c ,

h A sh        m , ssss которая вполне адекватно отражает свойства реальных декаметровых каналов связи, что подтверждается высокой степенью соответствия ее статистических характеристик экспериментальным данным.

Здесь Ac(s) – постоянный коэффициент; mc(s) – величины, определяющие математическое ожидание hc(s)(τ), γc(s)(τ) – независимые (в общем случае векторные) гауссовские марковские случайные процессы, задаваемые стохастическим дифференциальным уравнением вида d cs n                                                  (4)

_d            cs cs         cs cs    ,                                           (4)

где β c ( s ) – переменный параметр, обратный времени корреляции.

Для упрощения расчетов примем A c ( s ) = 1; m c ( s ) = 0.

При моделировании целесообразно в стохастическом дифференциальном линейном уравнении (4) перейти от непрерывного времени к дискретному. Для этого отрезок [0, τ ] разо-max бьем n эквидистантно расположенными точками tv = νΔ, где Δ = τmax/n – шаг дискретизации по времени, ν = 0,1,...,n. Для достаточно точной оценки результатов зададим n = 1000; τmax = 1 мс согласно [6].

Тогда для выражения (4) разностное уравнение принимает вид exp                 D 1/2 n ,

(v1)cs              cs vcs cs          vcs, где nνc(s) – белый гауссовский шум формирования, в качестве которого в модели взяты реализации датчика гауссовских случайных чисел.

Дисперсия белого гауссовского шума равна

D            2N /4      1 exp 2     ,(6)

cs           cs    0cs      cscs где N0c(s) – односторонняя спектральная плотность БГШ.

Описание основных результатов исследования

Вычислив дисперсию белого гауссовского шума согласно (6), задаваясь начальным значением γ c ( s ) (0) = 0, реккурентно вычисляем γ (ν+1) c ( s ) по γ ν c ( s ) в соответствии с выражением (5). Полученные таким образом значения γ c ( s ) представлены в виде графиков на рис. 1 а , б , при этом амплитуда Y c ( ₅ ) нормировалась к D c ( ^ ) .

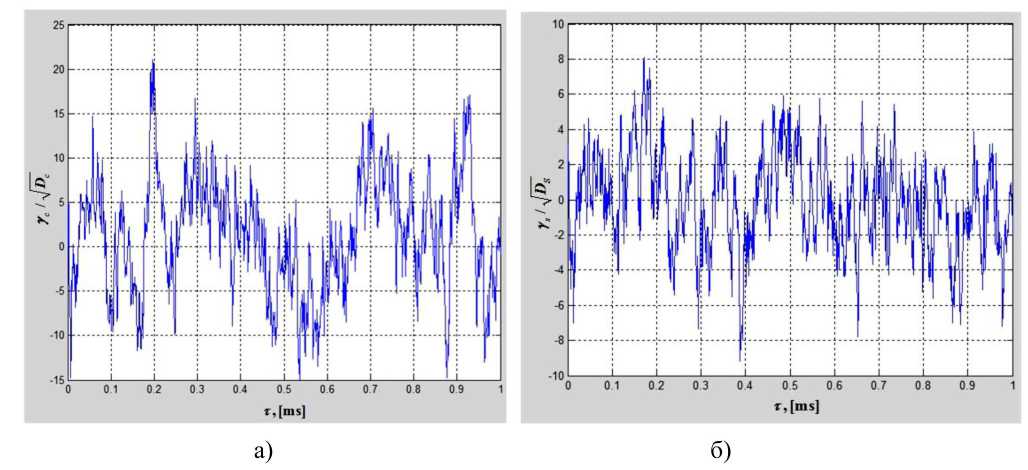
Рис. 1. Графики независимых гауссовских марковских случайных процессов у c(s )

С учетом того, что преобразование (4) является невырожденным, нелинейным, h c (τ) и h s (τ) также будут марковскими процессами [8].

Затем, подставляя полученные результаты из (5) в (2) и (3), находим квадратурные составляющие импульсной характеристики h c (τ) и h s (τ). Результаты моделирования представлены в виде графиков на рис. 2 а, б.

Так как характер замираний в декаметровом канале постоянно меняется, процессы h c (τ) и h s (т), очевидно, можно считать стационарными только на непродолжительных интервалах времени, соответствующих замираниям, описываемым определенным законом распределения с постоянными параметрами. Поэтому в общем случае параметры формирующего фильтра (4) будут зависеть от текущего значения времени. Согласно экспериментальным данным [9] период квазистационарности декаметрового канала связи составляет т_с = 5-15 мин.

Затем, подставляя полученные результаты из (2), (3) в (1), вычисляем импульсную характеристику канала связи. Амплитуда выбросов импульсной характеристики и ее квадратурных составляющих нормировалась к среднеквадратическому отклонению σ.

Основное требование к выбору и обоснованию математической модели декаметрового канала связи определяется величиной априорной погрешности моделирования, возникающей вследствие неадекватности реализуемой модели статистическим характеристикам реального канала связи.

Поскольку типичный декаметровый канал связи в точке приема согласно экспериментальным данным [10] преимущественно имеет 2-4 луча распространения, то в рассматриваемой модели предлагается из всех возможных компонентов многолучевости учитывать только те, которые являются существенными, что определяется их пересечением выбранного соответствующим образом порогового уровня.

Количество разрешенных компонентов многолучевости K per может быть идентифицировано из функции модуля импульсной характеристики (1) с учетом установленного порогово-

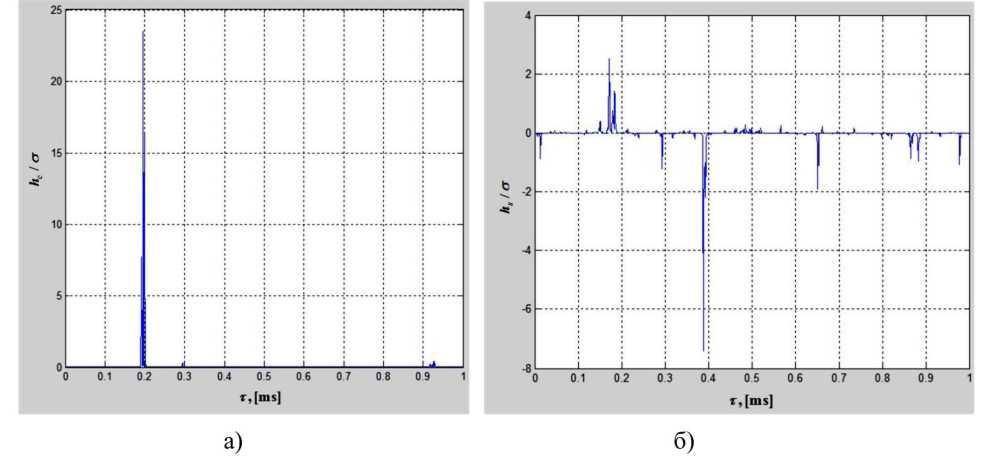
Рис. 2. Графики квадратурных составляющих импульсной характеристики hc ( s )(т)

го уровня. Рекомендованное значение порога, используемого для идентификации количества компонентов многолучевости, зависит от динамического диапазона измерительного оборудования и составляет уровень 15 дБ от максимального значения амплитуды импульсной характеристики [11].

На рис. 3 а и б представлены графики импульсной характеристики для одной из реализаций без учета порога идентификации и с учетом порога идентификации компонентов многолучевости соответственно.

Для выбора адекватной модели импульсной характеристики производим анализ комбинаций возможных значений параметров корреляции в c ( _s ) . Для каждой такой комбинации вычисляем вероятность пересечения заданного порогового уровня 2-4 выбросами импульсной характеристики. Требуемое значение такой вероятности составляет P_per ≥ 0,9.

Результаты моделирования, изображенные в виде объемной диаграммы на рис. 4, позволили установить значения параметров корреляции, при которых обеспечивается выполнение определенных выше требований к адекватности модели β c = 4 и β s = 25 с P = 0,91.

Заключение

Таким образом, в статье рассмотрена усовершенствованная марковская феномено -логическая модель импульсной характеристики декаметрового канала связи. Модель по -зволяет осуществлять идентификацию разрешенных компонентов многолучевости путем анализа комбинаций возможных значений параметров корреляции. Полученная таким образом импульсная характеристика с фиксированными статистическими параметрами формирует адекватную модель канала связи в течение каждого периода квазистационар -ности.

В дальнейших исследованиях предлагается полученную модель импульсной характеристики использовать для формирования на ее основе субоптимального фильтра, обеспечивающего обработку сигналов в декаметровом канале связи в условиях многолучевости.

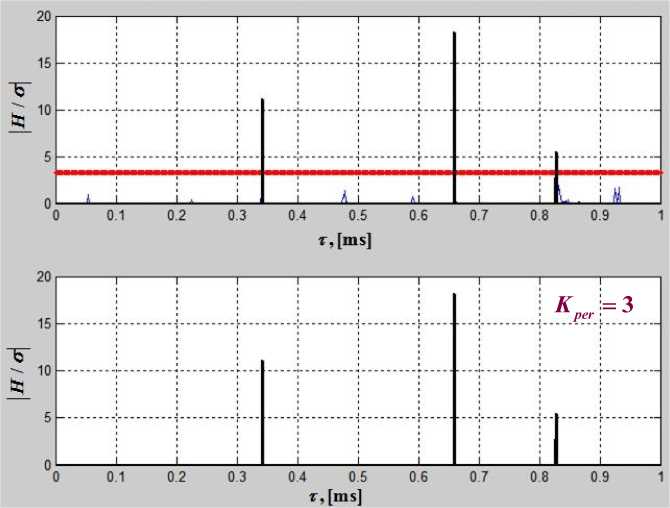
Рис. 3. График импульсной характеристики: а – без учета порога идентификации; б – с учетом порога идентификации

а

б

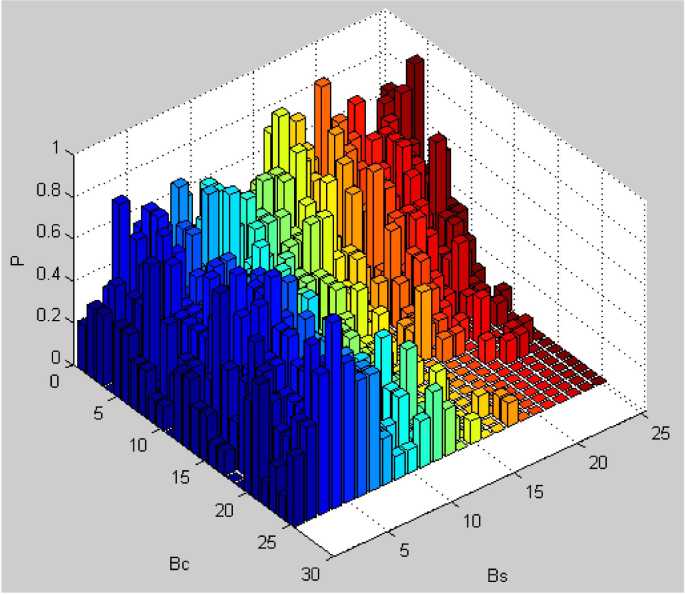
Рис. 4. Диаграмма проверки адекватности модели при различных комбинациях в c ( s )