Модель электромагнитного излучения в воздушной среде высокотемпературной сферически симметричной плазмы

Электромагнитные излучения в воздушной среде высокотемпературной плазмы формируются потоками электронов, инициируемых гамма-квантами, рентгеновским излучением, термоэлектронной эмиссией, процессами соударений молекул высокой энергии.

Излучения комптоновских и дельта-электронов, наведенных поглощением гамма-квантов в воздушной среде, хорошо изучены и систематизированы в работах [4; 5]. К таким излучениям относятся:

• •    геомагнитный импульс (закручивание комптоновских электронов в магнитном поле Земли [5]);

• •    поверхностный компонент излучения (асимметрия комптоновских токов при достижении поверхности Земли [Там же]);

• •    барометрический компонент (изменение длины пробега гамма квантов с высотой [1; 4]);

• •    асимметричный компонент (неоднородность излучения гама квантов по телесному углу [5]);

• •    микродипольный компонент (возникновение микродиполя электрон-ионов в момент ионизации молекулы [Там же]).

Влияние проводимости воздуха на формирование излучения перечисленных компонентов проанализировано в источниках.

Однако самым энергетическим компонентом является низкочастотное излучение высокотемпературной плазмы. На наш взгляд, электромагнитное излучение в диапазоне очень низких частот имеет более широкое применение, например, излучение разруша-

160 в ыпуск 2/2020

ющихся болидов в атмосфере Земли, излучение разрушающейся шаровой молнии и т.п. Рассмотрим модель такого излучения.

Будем считать плазменное образование сферически однородным с резко выраженной границей, изменяющейся во времени. Для высокой температуры плазмы из ее границы будут инжектироваться электроны, вызванные столкновениями высокоэнергетических молекул, термоэлектронной эмиссией, рентгеновским излучением. Скалярный потенциал, вызванный движением электрона в воздушной среде в точке R , будет равен [1]:

ф( R )=

Ve

4 п c е ₀ R² ’

где V – скорость движения электрона; е – заряд электрона; с – скорость света; ε0 – диэлек- трическая проницаемость вакуума; R – расстояние между корреспондентами.

Поскольку вылет электронов относительно радиуса плазмы RП сферически симметричен, а сам полный заряд равен нулю, то следует ожидать уменьшения скалярного потенци- ала всей плазменной сферы

τ

ϕΣ (R) ≈

τρ VeR _Π ³ 3 Tc ε ₀ R ^{2 ,}

где Т – отношение времени жизни электрона τ к одной секунде Т; ρ – изменение потока электронов с границы плазмы во времени.

Выражение (1) описывает потенциал нейтрально заряженной плазмы, как бы окруженной «облаком электронов». Эти электроны постоянно рождаются и прилипают к молекулам воздуха, но в области больших времен это «облако» можно рассматривать как постоянное окружение. Суммарный заряд «плазма – облако электронов» нейтрально, но разница расстояний между границей плазмы и «облаком электронов» создает незначительный потенциал (1). Такую систему (1) назовем всенаправленным диполем.

Выражение (1) получено в предположении очень низких частот, когда влиянием временного запаздывания ^Π можно пренебречь. Выражение (1) не учитывает влияния проводимости плазмы на компонент потенциала с тыльной стороны сферического образования. Однако, учитывая малость ^Π , выражение (1) можно считать справедливым для дальнейших расчетов. Векторный потенциал можно не учитывать, поскольку он равен

VV

[5] А = —ф _Е( R ) в силу отношения —< 10 - 10 (для энергии вылетевших электронов

cc менее 20 эВ).

Электромагнитное излучение системы (1) в силу симметрии будет отсутствовать. Нахождение в воздушной среде молекул воды может значительно усилить само электромагнитное излучение системы (1). В воздушной среде находятся взвешенные капельки или одиночные молекулы воды, которые ориентируются вдоль линий напряженности электрического поля потенциала (1) и создают электромагнитные микродипольные излучения, формирующие напряженность электрического поля обратно расстоянию от источника. Под воздействием напряженности электрического поля от потенциала (1) на капельке воды размером l формируется дипольный момент

4 πρτ e ε R _Π ² l ³ d =

3 TcR ³

где ε – относительная диэлектрическая проницаемость воды.

Чудновский Л.С. Модель электромагнитного излучения в воздушной среде...    161

На больших расстояниях L >  R излучение диполя в точке наблюдения L будет равно

E ( t ) = ^ 4 n c ² L £ 0

.

Для оценки излучения системы диполей (2)–(3) учтем изменение концентрации капелек с высотой h в сферической системе координат:

h          r cos O h

l (h ) = l3 e H = l3 e  H e Н, где Н = 6,3 км – приведенная высота концентрации капелек в атмосфере [3].

Величину плотности объема l ³ оценим из распределения удельной влажности 2–4 г/кг [2].

Поясним усиление электромагнитного излучения присутствием капелек воды. В сферической системе координат элемент объема dV = dRd θ d φ R ²sinθ. В подинтегральном R cos θ

- 1

выражении от расстояния остается множитель Re ^H . Именно этот множитель обеспечивает большой эффективный радиус интегрирований по переменной R до 5–10 км. Излученный электромагнитный сигнал становится низкочастотным.

Был проведен модельный расчет напряженности электрического поля от системы микродиполей с учетом запаздывания и интегрированием по объему излучения (рис. 1). Расстояние меду корреспондентами было выбрано 100 км. Приемник расположен на поверхности Земли. Начальная температура плазмы около 5 · 10⁵ К. Основным механизмом инжекции электронов полагались процессы столкновения между молекулами/ионами. Расчеты проводились для модельной функции возбуждения электронов At ² exp ( p t ^2/3 ) .

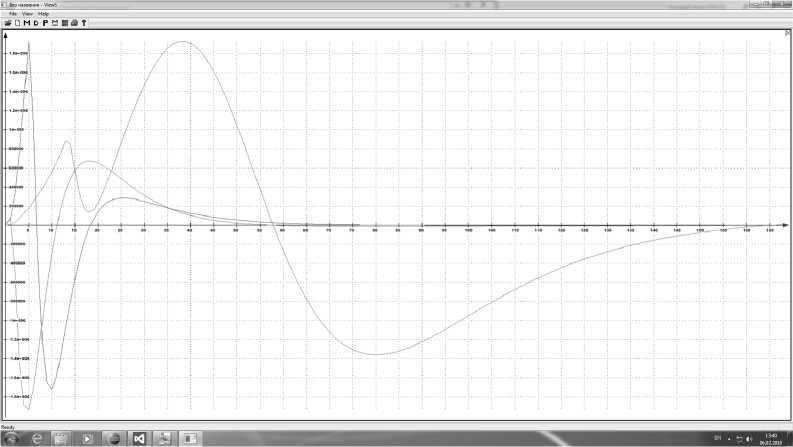
Рис. 1. Электромагнитное излучение высокотемпературной плазмы в воздушной среде для высот источника 700 м (первый импульс отрицательный), 3 км (первый импульс положительный) и высоты 8 км (первый импульс положительный с двумя максимумами). Время в одной клетке 10 мкс, амплитуда в относительных единицах

162 Выпуск 2/2020

Данные рисунка 1 демонстрируют смену полярности излучения для высот около 1,5– 2 км, увеличение длительности излучения с высотой источника. Характерные времена изменения излучения около 10 мкс, что соответствует размеру излучаемой зоны более 3 км. Данные рисунка 1 хорошо совпадают с данными экспериментов (но только для низкочастотной области безучета других компонентов излучения). Следует отметить более короткую длительность излучения на больших высотах h , что потребует дальнейшего уточнения модели в части изменения поверхности высокотемпературной плазмы.

Перейдем к объяснению смены полярности первого казипериода с увеличением высоты h . При малых высотах h доминирует одно направление диполей, поэтому первый кази-период отрицательный (см. рис. 1). На больших высотах h плотность диполей в области ниже высоты источника будет больше, а в области выше высоты источника h плотность будет меньше. Поэтому формируется положительный первый казипериод.

Объясним линейное фронтовое вступление длительностью (рис. 2). Точка приема расположена на Земле и удалена на расстояние L > h. Моменты диполей d2 и d4 не вносят вклада в излучение. Моменты диполей d1 и d3 тоже компенсируют суммарную электри- ческую напряженность электрического поля, но разность их времен прихода составляет t = 2R/с. Это обеспечивает почти линейное фронтовое вступление. С увеличением высоты источника дипольные моменты не равны друг другу d4 > d2. Поэтому на больших высо-h тах источника при приближении t к величине к линейной зависимости подключается параболическая зависимость (см. рис. 1). c

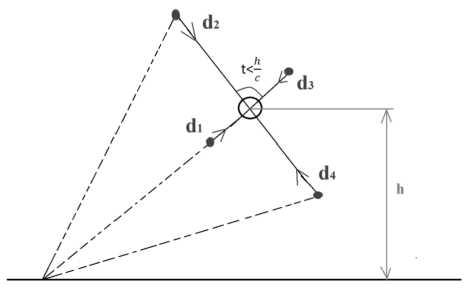
Рис. 2. Пространственное расположение диполей капелек воды (наблюдатель на поверхности Земли)

Наличие минимума на первом казипериоде на больших высотах h объясняется краткосрочной асимметрией в ориентации диполей для времен t >  h / c .

Сформулируем краткие выводы. Предложенная модель излучения правильно описывает изменения с высотой источника. Модельная временная функция возбуждения электронов с поверхности плазмы нуждается в дополнительном уточнении. При этом необходимо учитывать степень ионизации плазмы и ее начальный радиус развития.