Модель эволюции энергии в природно-технических системах

Состояние природно-технической системы (ПТС) определяется полной энергией системы. Здесь под понятием "состояние" понимается естественное состояние, к которому будет возвращаться система, освобожденная от внешних нагрузок. Изменение состояния описывается изменением полной энергии. Энергия любой ПТС с математической точки зрения не является линейной, ибо она содержит как элементы накопления, так и элементы ее диссипации, которые не обязаны быть линейными. Рассеивание энергии возникает в результате ее взаимодействия с потоком энергии другого природного происхождения. Например, рассеивание механической энергии происходит в результате ее взаимодействия с потоками тепловой, электрической, магнитной и других видов энергии [1].

Постановка задачи

Пусть эволюция напряженно-деформированного состояния некоторого участка массива горных пород ПТС зависит от ее энергии деформирования, накапливается и диссипирует. Рассмотрим систему уравнений

— = Ф 1 ( N - S) + / 1 ( t , N , S) dt

dS

— - Ф2(N - S) + /2 (/,N, S) dt где ^ – накопление энергии деформирования; S – диссипация; (^ – S) – полная энергия деформирования; φ1, φ2 – некоторые функции времени t; f1, f2 – функции внешнего силового воздействия.

Решение задачи, обсуждение результатов

Вычтя из первого уравнения (1) второе, получим:

^{d l N S 1} = (_Ф 1 - _Ф 2 )( _N - S )+( f l - f 2 ) . dt

Если обозначить ( N - S ) = W , ( ф 1 - ф ₂ ) = p , ( f 1 - f ₂ ) = q , то (2) можно представить в виде:

dW

"dT = ^{pW + q}

Это линейное дифференциальное уравнение [2], решение которого представляется зависимостью:

W = e ^ pdt ( C + J qe ^ pdt dt ) ,

где постоянная интегрирования C определяется по начальным значениям.

Исследуем несколько частных случаев. Из (4) получаем:

W = u + uv ,

pdt          1      - pdt                                   pdt u                           u где u = Ce , v = —J qe J dt. Следовательно, eJ   = — , или J pdt = ln— , после интегрирования

1 du последнего выражения получаем: p = u dt

.

Будем считать, что функция u пропорциональна времени плюс некоторая функция времени, т. е.

u = t + g ( t ) .

При этом имеем:

p ■ T+g t + g

.

Здесь и далее точка над функцией означает производную по времени.

Полагаем также, что функция v

e ^{- g}                 1       - pdt           q        e ^{- g}

---, тогда v = qe ¹ dt =      dt =--- . Отсюда находим C           C            t + g C

q = -( t + g ) ge" g .

Таким образом, окончательно

W = ( t + g )(1 + e - ^g ) .

Рассмотрим примеры.

Пример 1 . Пусть u = t + arcsin(sin t ) . График этого выражения представлен на рис. 1.

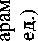
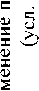
Рис. 1. Изменение параметра u = t + arcsin(sin t )

Вестник МГТУ, том 19, № 1/1, 2016 г. стр. 35–39

- ( ⁿ+ arcsin(sin t ))

Полагаем v = e ²         . На рис. 2 приведен график этой зависимости.

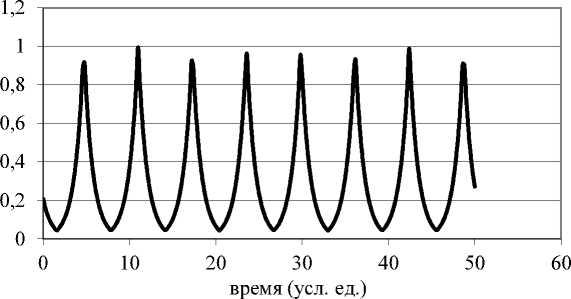
Рис. 2. Изменение во времени параметра v

Рассмотрим ПТС, энергия которой с начала ее существования и до последнего момента имела "взлеты" и "падения".

Пусть функции, входящие в (1), имеют вид:

1                            - cos t

Ф1 =-------:—:---; ф2 = .       =------------------

^T + arc^sin(sin / ⁾         Vl - sin ² 1 ( t + arcsin(sin t ))                                         )

COS t      ^{- (}Varcs™™ t))                   . .          COS t      ^{- ( П}+ a'csmlsm t))

/ = t           e ²          ; / 2 =- arcsin(sin t )            e ²

_       V1 - sin ² 1                                      VI - sin ² 1

Тогда после преобразований, приведенных выше, получаем

W = ( t + arcsin(sin t ))

П

1 + exp( - — - arcsin(sin t )) .

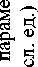
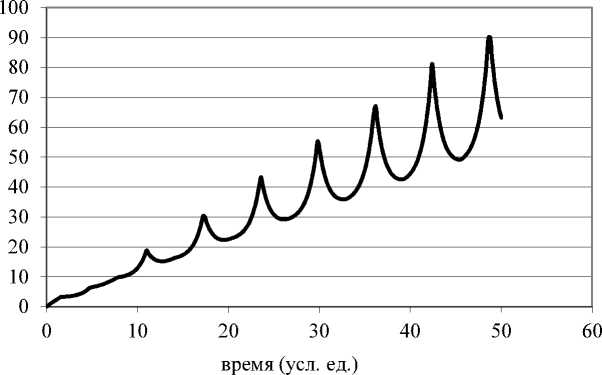
Рис. 3. Периодическое изменение энергии ПТС

График этой зависимости представлен на рис. 3. Если при каком-то значении времени t ₀

выражение (11) дополнить зависимостью

W = [ (2 t ₀ - 1 ) + arcsin(sin t ) ]

n

1 + exp(- — - arcsin(sin t ))

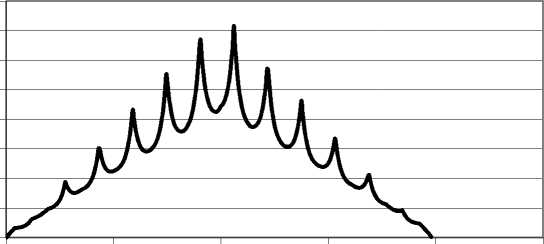
то график суммарного выражения (11) и (12) будет иметь вид, приведенный на рис. 4.

0         20         40         60         80        100

время (усл. уд.)

Рис. 4. График изменения удельной энергии деформирования ПТС с "взлетами" и "падениями"

Здесь принято t 0 = 40 (усл. ед.). Такая эволюционная зависимость может быть условно перенесена на "жизнь" некоторого живого организма, которая характеризуется "периодическими взлетами и падениями".

Пример 2 . Пусть функции, входящие в (1), имеют вид:

Ф , = 1 + + sin t ; n

Ф 2 =

2     2 t 4 t

(cos + cos ) ;

3       15

П

f = - t^g exp( - g ) ; f = gg exp( ^- g ) ; g = Ф 1 -ф ₂

После необходимых преобразований (13) получаем:

2     2t4

и = t + (1,31831 + 0,5sin t — (cos — + cos ) ;

n     315

n                        2     2t v = exp( -(1,31831 + 0,5sint — (cos — + cos )));

2                     n     315

W = u (1 + v) .

График функции W ( t ) представлен на рис. 5. Из рисунка видно, что энергия ПТС имеет различные величины подъемов и падений, в зависимости от способов накопления и диссипации. Эта зависимость напоминает экспериментальные данные по изменению акустической эмиссии при нагружении образца горных пород [3].

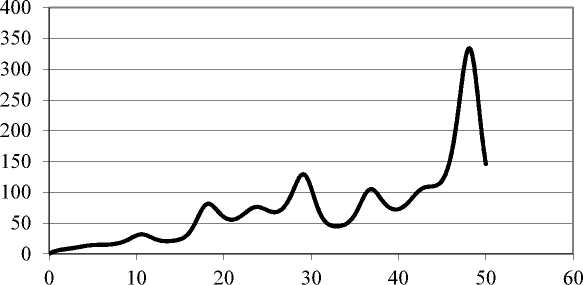
время (усл. уд.)

Рис. 5. Зависимость W ( t ) по (14)

Рассмотрим уравнение (3) и его решение (4) с несколько другой точки зрения.

1 ⁿ

Пусть p = -      , q = ^ [ W i ] 5 ( t , ) ,

t +1      in где [Wi] – импульс i-го отклика в момент времени ti продолжительностью τi. Например, W0 = 20; t1 = 5; t2 = 12; t3 = 16; t4 = 20; t5 = 25; [W1] = [W2] = [W3] = 3; [W4] = [W5] = 5; τi = 0,1.

Вестник МГТУ, том 19, № 1/1, 2016 г. стр. 35–39

Решение (4) при этом имеет вид:

I                                                                                                                        I w=К+£ [w ] (t- + 1)T-r. t+11       -=i                  I

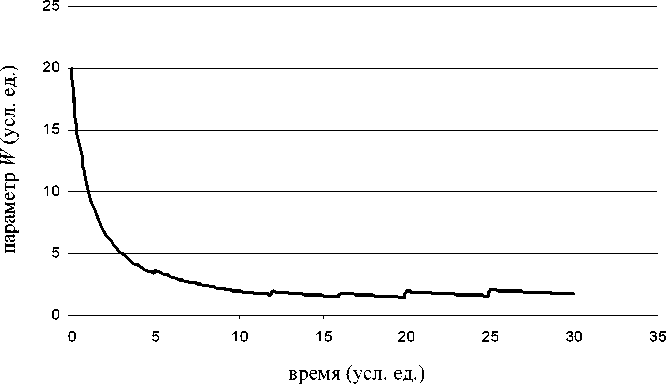
Рис. 6. График зависимости (16)

Такую ситуацию можно рассматривать как некий отклик массива на массовый взрыв. В моменты времени t _i происходит образование трещин с выделением некоторой величины энергии.

Выводы

• 1.    Характер изменения упругой энергии деформирования природно-технической системы в математической форме представляется системой обыкновенных дифференциальных уравнений с коэффициентами, зависящими от времени.

• 2.    Эволюция энергии деформирования природно-технической системы зависит от скорости накопления и диссипации энергии в процессе природного или техногенного изменения внешнего воздействия.

• 3.    Энергия деформирования эволюционирующей системы может характеризоваться "подъемами" и "падениями" в зависимости от того, в какие моменты времени происходит большая часть накопления по сравнению с диссипацией или наоборот.