Модель неупругого деформирования ОЦК-поликристаллов с учетом двойниковой моды деформирования. Численное моделирование некоторых процессов деформирования

Поведение материалов на макроуровне определяется эволюцией мезо - и микроструктуры, поэтому актуальной задачей является построение моделей неупругого деформирования моно - и поликристаллов , основанных на физических теориях пластичности. В основе формулировок определяющих соотношений, гипотез и основных положений этих теорий лежит рассмотрение в явной форме механизмов деформирования на мезо - и микромасштабах. Для описания структуры и механизмов деформирования на мезо - и микромасштабах используются параметры, называемые внутренними переменными, которые характеризуют эволюционирующую микроструктуру материала и содер-жат информацию об истории воздействий на материал [1].

В моделях, основанных на физических теориях, обычно рассматривается один механизм деформирования - внутризеренное скольжение краевых дислокаций. Несмотря на то, что двойникование не является преобладающим видом неупругого деформирования в материалах с большим числом систем скольжения (ГЦК- и ОЦК-кристаллах), экспериментально установлено, что деформирование двойникованием имеет место во многих ОЦК (ГЦК)-металлах с низкой энергией дефекта упаковки при низких гомологических температурах. Двойниковые прослойки служат препятствиями для движения дислокаций и приводят к существенному изменению отклика материала. Учет двойниковой моды деформирования приводит к качественному и количественному измене -нию отклика материала, что обусловливает необходимость ее моделирования . Для описания предлагается использовать двухуровневую (мезо- и макроуровни) математическую модель; элементами мезоуровня являются кристаллиты (зерна, субзерна), макроуровня - представительный макрообъем ; характеристики мезоуровня обозначены строчными буквами, аналогичные параметры макроуровня - прописными.

Кинематическое описание деформирования мезоуровня прово-дится с использованием четырех конфигураций: отсчетная K0, две промежуточные K*, K** и текущая (актуальная) Kt. Градиент места flin описывает неупругое деформирование материала скольжением дислокаций, переводящим отсчетную конфигурацию К0 в промежуточную K*. Градиент места fw описывает неупругое деформирование двойникованием, преобразующим промежуточную конфигурацию K* в промежуточную K**. Градиент места fe отражает упругое деформирование и переводит промежуточную конфигурацию K** в текущую Kt. Используется мультипликативное разложение транспонированного градиента места («градиента деформации») f=VrT (V - набла-оператор, определенный в отсчетной конфигурации, r - радиус-вектор частиц) на упругую fe и неупругие f5n, ftw составляющие:

e in in

f - f f tw f 5 •

Определение градиента скорости перемещений l и соотношение (1) позволяет показать справедливость следующего разложения:

r e -1 _ i e ii in .1 in

* f    “l +l tW ⁺¹ 5 ,

. re rin bin rin—1 erin—1 f  ftw fs  fs    ftw ie _re re—1 tin re rin inin—1 re—1 iin re rin rin rin—1 rin—1 re—1

где l =^{f f} , l tw =^{f   f} tw ^f tw   ^f , l 5 =^f t tw f 5  f 5 f tw   f .

Введем обозначения

06 .                   06       .

1 ** in — fin rin -1 1** in — fin bin _efin- 1 _e fin- 1 l tw     ^vtw t^tw , l 5      twv ¹5 *5     ¹tw

.

Тогда соотношение (2) перепишется следующим образом:

1=1 ^e +f e . ff* in₊ 1** in \.f^¹ tw s

.

Внутризеренное скольжение краевых дислокаций по системам скольжения (СС) является основным механизмом неупругого деформирования кристаллитов. В ОЦК-кристаллах скольжение всегда происходит в наиболее плотно упакованных направлениях <111>, а плоскостями скольжения могут быть плоскости {110}, {112}, {123}.

Системы скольжения в К₀ и K _t определяются ориентационными тензорами:

( o( ^k )

m

(k) ¹ h b

0 2

o( ^k )

n

o

n

m

t k ) =1 f e. b

o( ^k )

o( ^k )

n

( k ) o( k ) )

b , k =1,..,48,

o( k ) o( k ) )

+n b     f " e , k = 1,..,48,

o( ^k ) o( ^k )

где b , n - единичные векторы направления скольжения и нормали k -й системы скольжения в отсчетной конфигурации.

В физических теориях не рассматривается движение отдельных дислокаций, их распределение предполагается однородным по элементу мезоуровня (зерну, субзерну), что дает возможность рассмотрения неупругой составляющей тензора деформации скорости от скольжения краевых дислокаций в виде

Ns din^ikm1 k|,                         (4)

k где уk - скорость сдвига по k-й системе скольжения.

Условием активации k -й системы скольжения является достижение касательного напряжения в ней некоторого критического напря-жения т k ; данное условие называется законом Шмида:

k тcs =m^:o ,                           (5)

где о - тензор напряжений Коши (однородный по рассматриваемому кристаллиту).

Другим механизмом неупругого деформирования является двой-никование. Отметим, что двойникование может не вносить большого вклада в неупругую деформацию, но играет весьма важную роль в процессе скольжения краевых дислокаций - основного механизма неупругого деформирования. Процесс двойникования будет рассматриваться подобно скольжению краевых дислокаций. Используя две конфигурации кристаллита: отсчетную конфигурацию (монокристалл находится в недеформированном состоянии) и актуальную (в монокристалле появляются несколько двойниковых прослоек), можно показать, что осредненный (по кристаллиту) градиент места, описывающий формоизменение двойникованием, имеет следующий вид:

^f tn^^tw b tw n tw +^E ,

где E - единичный тензор; b tw - направление сдвига двойника; n tw -нормаль к плоскости двойникования; f - представляет собой безразмерную величину, равную отношению объемов двойниковых прослоек , в которых произошел сдвиг, к объему всего кристаллита (объемная доля двойников); y tw - величина постоянного сдвига двойника, равная для ОЦК-кристалла 0,707.

Полагая, что двойникование происходит непрерывно, f существует и конечно, осредненный градиент скорости перемещений двойникования для монокристалла можно записать в виде [2]

. ** in l tw

=f in . f in- bn = Tv t

¹tw ^Atw     J t tw^utw¹¹tw J ttw^v .

Таким образом, двойникование может рассматриваться как «псевдоскольжение» со скоростью «двойникового» сдвига f y _tw и ориентационным тензором t=b _tw n tw . Далее для каждой к -й системы двойникования введем обозначение симметричного ориентационного тен-зора t ^(к) :

*(k)-1 ee(ь(k) n(k) + n(k)b(k)1 e-e t 2f ^btw ntw +ntw btw Д ,k T-,12-             (8)

Дислокационный механизм двойникования позволяет записать неупругую составляющую тензора деформации скорости, связанную с двойникованием, в виде, аналогичном (4):

Ntw dw^fklwt1k1 -k

Условием активации k -й системы двойникования является достижение касательного напряжения в ней некоторого критического на -пряжения т k_tw ; соотношение, аналогичное закону Шмида (5):

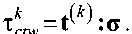
N s          Ntw d”=d in+d inw^m *'+^ f   t( *'.          (ii)

kk

На макроуровне рассматривается представительный объем поли -кристаллического металла, состоящий из совокупности элементов мезоуровня . Конститутивная модель материала на макроуровне записывается в виде

S r ±+Q T-И +L Q = C:D e = C: ( D-D iⁿ ),

П П(о( , ■), C( , ■ A i = 1,..., N ,

< V ’                                             (12)

C = C(C( i )), i = 1,..., N ,

Din = Din(din), C(0),i = 1,...,N, где S - тензор напряжений Коши, С - тензор модулей упругости, D, De, Dn - тензор деформации скорости, его упругая и неупругая составляющая , индекс r означает независящую от выбора системы отсчета производную, Я - тензор, описывающий движение подвижной системы координат, относительно которой определяется собственно деформационное движение [3] на макроуровне. В данной работе для определения О и Din предлагается использовать условия согласования определяющих соотношений на различных масштабных уровнях [4, 5].

Двухуровневый подход предполагает использование структурно -го элемента мезоуровня - кристаллита (зерно, субзерно, фрагмент). На мезоуровне в качестве определяющего соотношения также использует -ся закон Гука с учетом анизотропии кристаллической решетки [6]:

О r = c:d ^e = c: (d-d in ),

V )                          (13)

оr =6-gj o+o ta, где о - тензор напряжений Коши; or - коротационная производная тензора напряжения Коши; с - тензор четвертого ранга упругих свойств ОЦК-кристалла (кубическая симметрия); d, de, din - тензор деформации скорости, его упругая и неупругая составляющие; го - тензор спина, характеризующий скорость вращения кристаллической решетки . В данной работе тензор спина определен в соответствии с моделью Тейлора [7]. Отметим, что напряжения характеризуют именно упругие связи в зерне, связанные с изменением расстояний

между соседними атомами.

Система разрешающих уравнений для кристаллита в скоростях имеет следующий вид:

a = c:(d-d ^/и )+(оо-ош,

N s        N tw di^ykm k + ^f4w tk,

k

k d = D,

Ns

¹ V v- V v ^r -AjTy k n ⁽ k ) b ⁽ k ) b ⁽ k ) n ⁽ k ) , 2^х j 2'

t“

s

I                     12         •

, kW^fT/ltj', i=1

^k s H

^k s ^k

s

1/m signOk), fk =

Y о C.

vl к

/ V, T\ tw tw о, 4 <0.

1/ m

k

, W — ^o,

Здесь (14)1 - закон Гука в скоростной релаксационной форме с учетом геометрической нелинейности;

(14)2 - кинематическое соотношение;

• (14)з - гипотеза Фойгта (D - тензор деформации скорости макроуровня );

• (14)4 - соотношение модели поворота Тейлора;

• (14)5 - соотношения для скоростей критических напряжений сопротивления сдвигу т“ , и двойникованию i ktw ;

• (14)6 - упруговязкопластические соотношения для определения скоростей сдвига и изменения объемной доли двойников;

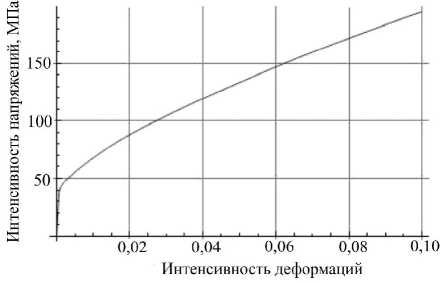
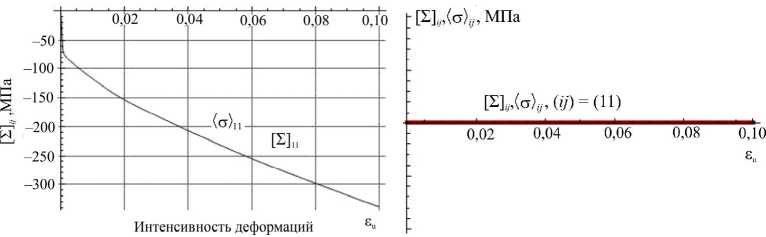
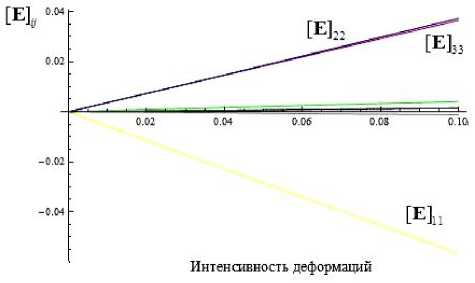
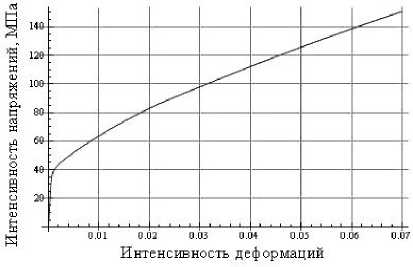
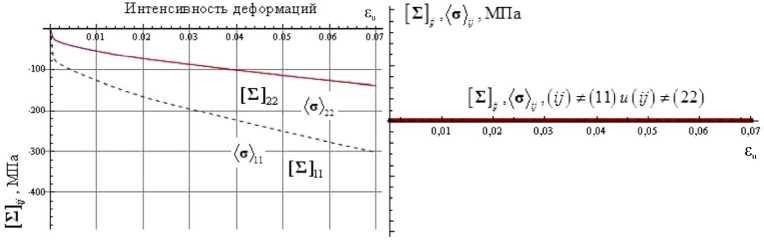
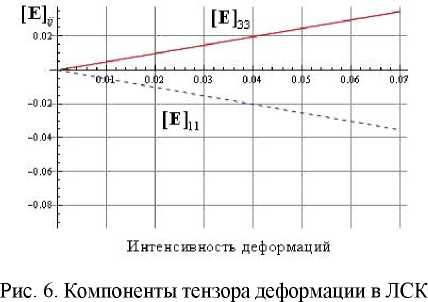
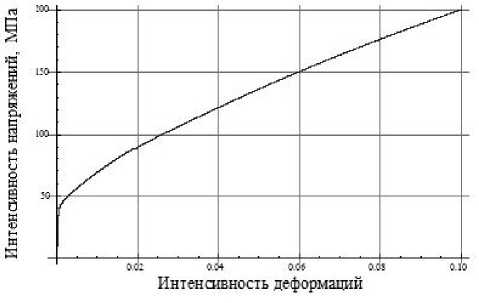
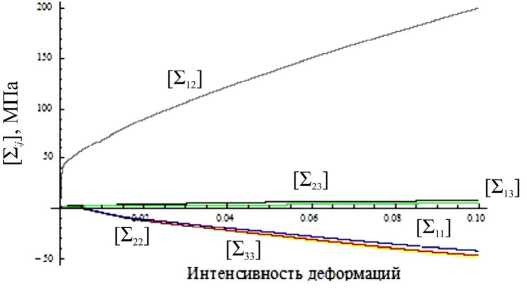
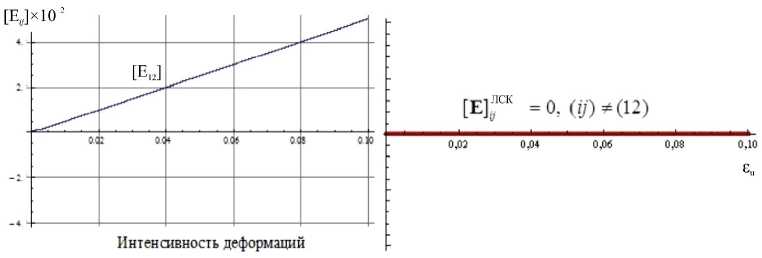
t +Q^T-S+L Q C:(D D in)                 (15)

и мезоуровня (для каждого элемента из выборки) в виде о-гоо+

Далее согласно [4, 5] представим величины, входящие в определяющие соотношения мезоуровня, в виде суммы средних по представительному объему макроуровня величин и отклонений от этих средних :

c =< c>+c', о=<о>+о\ d =< d > +d', din =< din >+din, щ =<ю >W, где < • > - оператор осреднения (вид которого не конкретизируется), обладающий свойством

• =0, <о>= 0, = 0, = 0, <щ'>= 0.(18)

Подставляя представление (17) в определяющее уравнение мезоуровня (16) и осредняя его, получаем соотношение

<Й> + <о>+<оT • o' > + <(D> + <о'•(!)'>= „        . , „(19)

= <с>:(-) + .

Далее принимается, что согласование напряженно-деформированного состояния на различных уровнях заключается в равенствах

С=<с> , L=, D=

Соотношение (20) устанавливает, что эффективные свойства и характеристики напряженно-деформированного состояния на верхнем масштабном уровне должны быть в точности равны осредненным характеристикам нижнего масштабного уровня.

В силу антисимметричности тензора го (т.е. при коротационных производных на мезоуровне в законе (16)) с учетом (20) соотношение (19) можно записать в виде

Ё- L+L - > + ,•w^, > =

= C:(D-in >)+<c:(d-din')>.

Тогда для согласования двух соседних масштабных уровней необхо-димо положить

Q =< и >, ,                           .                                (21)

Din =in > - C" 1:in)>- C" ^(«o V>-).

Следует заметить, что при таком подходе на макроуровне получается коротационная производная. Жесткую подвижную систему координат можно трактовать как некоторый трехгранник, соответствующий осредненной ориентации элементов мезоуровня, а осредненный спин £1 =<го > - как скорость его поворота.

В случае использования в статистических моделях для передачи на мезоуровень условий нагружения гипотезы Фойгта d = D, d'= 0 связи (21) принимают вид

£1 =<№>,

Din     iift          1                  /^^_1

= + C :-C :(-).

Тогда постановка задачи для представительного объема макро -уровня выглядит следующим образом:

± = C:(D-Diⁿ)+Q L-SU,

< Q ,                                                     (23)

Din =< din > + C 1: C 1:(-«/-e>'>), где C - тензор упругих свойств макроуровня, D - тензор деформации скорости макроуровня, Din - неупругая составляющая тензора деформации скорости макроуровня, £1 - тензор, входящий в независящую от выбора системы отсчета коротационную производную тензора напряжений макроуровня, S - тензор напряжений Коши, c', din ,<$',№' - отклонения от среднего (по представительному объему макроуровня) тензора упругих свойств, неупругой составляющей тензора деформации скорости, тензора напряжений Коши и спина решетки соответственно, <•> - оператор осреднения по представительному макрообъему.

• 5.    , , чистого сдвига

Рассмотрим постановки задач и результаты моделирования неко-торых процессов деформирования представительного объема (ПО) поликристалла , таких как осадка, стесненная осадка и чистый сдвиг.

Для реализации осадки материала на макроуровне должно быть выполнено условие одноосного напряженного состояния. Рассмотрим образец в форме прямоугольного параллелепипеда (в отсчетной конфигурации ) при расположении осей лабораторной системы координат (ЛСК) OX1, OX2, OX3 перпендикулярно соответствующим граням; поверхности контакта полагаются идеально смазанными. Для определенности рассмотрим сжатие вдоль оси ОХ\ фиксированной ЛСК. Использование гипотезы Фойгта предполагает жесткое нагружение на каждом шаге нагружения, предписанным является тензор деформации скорости . Условия одноосного напряженного состояния не позволяют задать все компоненты данного тензора, т.е. одноосное нагружение в исходной постановке нельзя вести чисто кинематически, поскольку граничные условия на макроуровне являются смешанными. В то же время для применения алгоритма решения на мезоуровне, основанного на гипотезе Фойгта, необходимо определять в каждый момент деформирования все компоненты градиента места (или градиента скорости перемещений ). Поэтому реализация одноосного растяжения (сжатия) в рамках модели осуществляется следующим образом: предписанной является только одна компонента тензора деформации скорости на макроуровне в ЛСК [D^ , а остальные компоненты [DJ. определяются в результате решения задачи исходя из необходимости обеспечения соот-ветствующего одноосного напряженного состояния: [Ё]у^{ЛС К}=0, (ij) ^(11). Отметим, что тензор деформации E определялся интегрированием тензора скорости деформации D, т.е. использовалась так называемая неголономная мера.

Постановка задачи одноосного растяжения /сжатия ПО макроуровня выглядит следующим образом:

± = C:( D - D ^ту£ЪУ.-У.-£1

£1 =< w >,

Din =<din> + C^l:'"'>-C"^(«o' o'>- и>),   (24)

Й^K=o, ®)#(11),

ГП1 ЛСК_ГП1 ЛСК предписанное

I [D]11     -[D]11                  .

Рис. 1. Диаграмма одноосного нагружения поликристалла ОЦК-железа

Рис. 2. Компоненты тензора напряжений Коши в ЛСК при осадке поликристалла ОЦК-железа

Из результатов, приведенных на рис. 1-3 видно, что реализуется одноосное напряженное состояние. Условия согласования ОС двух соседних масштабных уровней (17) обеспечивают полное соответствие между макронапряжениями и осредненными напряжениями мезоуровня.

Рис. 3. Компоненты тензора деформации в Л СК при осадке поликристалла ОЦК-железа

Перейдем к рассмотрению процесса стесненной осадки, который реализуется следующим образом: вдоль оси OXi происходит сжатие, вдоль одной из осей (для определенности OX2) перемещение запрещено . Как и в случае осадки, используется гипотеза Фойгта (предписанным является тензор деформации скорости). В случае стесненной осадки задаются две компоненты тензора деформации скорости на макроуровне в ИСК [D_|ц и [DJ22 = 0. Остальные четыре компонен ты [ DJ определяются в результате решения задачи из условии [±]/ск=0, (j>(11)«(j>(22).

Постановка задачи стесненной осадки ПО макроуровня с учетом согласования соседних уровней (мезо- и макроуровня) выглядит следующим образом:

±=C:( D - D ^ту£1Х.-У.-£1

£1 =<щ>,

Din =< din > + C ¹:in > - C" ¹:(«o^r V > - < o' W >),   (25)

C=(c),

[±]/^ск = 0, (ij)^(11)//(i/>(22),

ГП1 ЛСК-ГП1 ЛСКпредписанное. rnl ЛСК_П ([DJ11    — [DJ11                HDJ22    — 0.

На рис. 4-6 приведены результаты численного моделирования стесненной осадки ПО ОЦК-железа.

Рис. 4. Диаграмма нагружения поликристалла ОЦК-железа (стесненная осадка)

Рис. 5. Компоненты тензора напряжений Коши в ЛСК при стесненной осадке поликристалла ОЦК-железа

при стесненной осадке поликристалла ОЦК-железа

В отличие от предыдущих двух случаев (осадки и стесненной осадки) чистый сдвиг задается кинематически:

все компоненты тензора деформации скорости, причем отлична от ну-

Гп 1ЛСК левой только D 12 :

±=C:(D-Dinj+Q-L-L-Q

£1 = <(o>, in in 1                    /^—1

 + C :-C :(-),

C=(c),

[D]₁₁^JICK=[D]₁2^JICKпредписанное, [D]_ JICK₌q (^^(12) .

Результаты моделирования чистого сдвига ПО ОЦК-железа пред ставлены на рис. 7-9.

Рис. 7. Диаграмма нагружения поликристалла ОЦК-железа

Рис. 8. Компоненты тензора напряжений Коши в ИСК при чистом сдвиге поликристалла ОЦК-железа

Рис. 9. Компоненты тензора деформации в ЛСК при стесненной осадке поликристалла ОЦК-железа

Заключение

Представлена физическая упруговязкопластическая модель, в ко-торой учитываются две моды неупругого деформирования ‒ скольже-ние краевых дислокаций и двойникование, оказывающие существен-ное влияние на отклик материала при его неупругом деформировании. Использованы условия согласования определяющих соотношений со-седних масштабных уровней, обеспечивающие соответствие мер на-пряженного и деформированного состояний этих уровней. Предлагае-мая модель позволяет описывать неупругое деформирование ПО поли-кристаллов; представлены результаты расчетов для одноосного нагружения, стесненной осадки, чистого сдвига.

Работа выполнена при финансовой поддержке РФФИ (гранты 10-08-96010-р_урал_а, 10-08-00156-а).