Модель оценивания оперативности многопоточной обработки задач в распределенной вычислительной среде с учетом процессов Split-Join

Эффективность функционирования распределенных информационно-вычислительных систем определяется многими факторами, в том числе возможностями декомпозиции целевой задачи и параллельного выполнения подзадач. Примерами параллельного выполнения подзадач являются технологии параллельных запросов в реляционных системах управления базами данных [1], обработка изображений [4; 6; 7; 8; 9], поточная обработка больших данных на основе модели организации распределенных вычислений MapReduce и др.

Хабаров Р.С., Лохвицкий В.А. Модель оценивания оперативности многопоточной... 27

Как правило, для оценки оперативности распределенной обработки данных используется показатель качества обслуживания (QoS), определяемый как вероятность того, что среднее время обработки не превысит заданного с определенной вероятностью. Наиболее подходящими математическими моделями, позволяющими получить оценки оперативности подобных систем, являются системы с очередями [3].

Для описания процесса разделения задачи на потоки с параллельным их выполнением и последующим объединением результатов в теории очередей используют модель системы массового обслуживания (СМО) с дисциплиной Split-Join [5]. В такой модели (рис. 1) прибывающая в систему заявка разделяется на N подзадач, которые обслуживаются параллельно. Следующая прибывающая в систему (выбираемая из очереди) заявка поступает на обслуживание только после завершения обработки всех подзадач и агрегирования результатов текущей задачи.

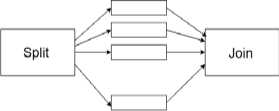
Рис. 1. Схема дисциплины обслуживания Split-Join

Изучению СМО с дисциплиной Split-Join посвящено достаточно большое количество работ. В одной из них [10] получено точное решение для максимума (времени обслуживания) независимых каналов с экспоненциальным временем обслуживания и различными интенсивностями, а также аппроксимации для случая распределения общего вида. В другом исследовании [11] упомянутое распределение получено для гомогенных и гетерогенных серверов, причем представление его в матрично-экспоненциальной форме позволило найти момент как первого, так и высших порядков. Надо отметить, что указанный способ характеризуется высокой вычислительной сложностью, являющейся следствием входящих в него трудоемких операций обращения и кронекерова произведения матриц. Применение кронекеровой алгебры связано со значительным дополнительным расходом памяти, а также множеством избыточных операций с нулевыми операндами. Кроме того, не учитывается время, затрачиваемое системой на чтение и запись данных, а также разбиение на подзадачи и сборку результатов.

Таким образом, актуальной представляется задача разработки модели, позволяющей оценить оперативность многопоточной обработки задач с учетом дисциплины Split-Join и временных затрат, связанных с декомпозицией исходной задачи, сборкой результатов, операциями чтения и записи данных.

Модель оценивания оперативности многопоточной обработки данных

Процесс параллельной обработки данных с возможностью их декомпозиции и слияния результатов может быть представлен в виде трех последовательных этапов:

• •    подготовка данных к параллельной обработке (включая чтение данных);

• •    параллельная обработка;

• •    агрегирование результатов с возможной записью данных.

28 Выпуск 1/2019

Представим процесс в виде открытой СеМО (рис. 2). Введем допущение, что входной поток поступающих в сеть заявок является пуассоновским. Поступающие из источника (узел S0) заявки попадают в узел подготовки данных к параллельной обработке (S1). Поскольку процесс подготовки может быть также распараллелен, данный узел представим в виде СМО типа M/G/n с дисциплиной обслуживания FCFS. В зависимости от особенностей вычислительной инфраструктуры количество узлов параллельной обработки может варьироваться, поэтому дальнейший путь заявки представим направленным графом, узлы которого представляют собой СМО с дисциплиной обслуживания Split-Join (S2.x.x), а переходы между узлами определены маршрутной матрицей сети, элементы которой представляют собой вероятности соответствующих переходов между узлами сети.

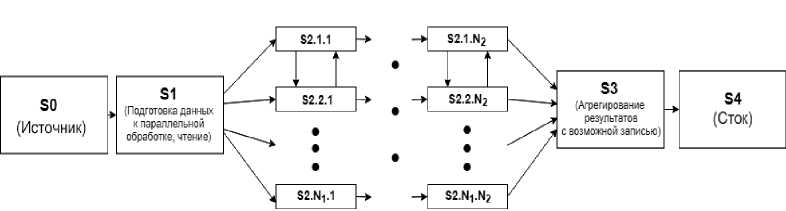
Рис. 2. Модель процесса многопоточной обработки данных

После завершения этапов параллельной обработки выполняется сборка результатов в S3, который также может быть представлен в виде СМО M/G/n. Далее заявка покидает сеть (узел S4).

Особую сложность представляет расчет характеристик многоканальной СМО с дисциплиной Split-Join, поэтому представим данный процесс в виде СМО M/G/1 на основе нахождения распределения максимума длительности обслуживания подзадач Для этого воспользуемся методом расчета начальных моментов искомого распределения через дополнительную функцию распределения (ДФР) максимума случайных величин на основе вычисления интеграла по полуоси с весом Чебышева – Лагерра. Данный метод позволяет получить искомые моменты сравнительно небольшим количеством вычислений и применим для случая гетерогенных каналов с произвольным законом распределения длительности обслуживания в канале.

Метод расчета моментов распределения длительности обработки задач в системе массового обслуживания Split-Join

Требуется рассчитать начальные моменты распределения длительности обслуживания заявки с учетом ее разделения на N потоков с последующим объединением результатов Искомые моменты { g m } могут быть выражены через ДФР максимального времени облуживания задач.

Хабаров Р.С., Лохвицкий В.А. Модель оценивания оперативности многопоточной... 29

Поэтому удобно практический расчет вести согласно

∞∞  ∞

gm = J tmdF(t) = m J tm-1F(t)dt = J tm-1(1 - F*(t))dt, m = 1,3,

0                   00

где F (t) - функция распределения максимума случайной величины, которая определя- ется согласно

F * ( t ) = п F ( t ).

_______                                           i = 1

Здесь F_t ( t ), i = 1, N - функция распределения времени обработки i -й задачи. Тогда

*

∞ gm = Jtm-1(F (t))dt, m = 1,3,

где F ( t ) - ДФР максимума времени обслуживания заявки в системе Split-Join.

Поскольку интеграл (2) может не иметь аналитического представления, воспользуемся формулой для численного вычисления интеграла по полуоси с весом Чебышева – Лагерра

[2]:

∞

n

J x s e ^{- Xf (} x ) dx ~ J A k f ⁽ x k ).

k = 1

Существуют справочные таблицы для { X k } и { A k } при различных значениях s и n [3].

Заменим обозначение x на t и представим функцию f ( t ) как F ( t ) e . Тогда выражение (2) для g_m может быть представлено в виде

.Д  —*

g m = m X ^Ak^{F (} ^ k ) e t k , m = ¹’²-

k = i

Рассчитанные с помощью формулы (3) моменты соответствуют моментам распределения длительности обслуживания параллельной обработки данных с учетом дисциплины Split-Join (узлы 2.x.x СеМО).

Пример использования модели для расчета оперативности многопоточной обработки изображений в распределенной вычислительной структуре

В области обработки изображений большинство задач может быть решено путем последовательного применения к обрабатываемым данным некоторого набора типовых операций обработки [8; 9]. Естественный при обработке изображений параллелизм, основанный на декомпозиции данных, позволяет адаптировать последовательные реализации широкого спектра задач обработки для их многопоточного выполнения, например, на многоядерных процессорах.

В распределенных системах обработки изображений существует два основных подхода к организации параллельной обработки:

• •    декомпозиция по данным (или пространственная декомпозиция);

• •    декомпозиция по задачам (функциональная декомпозиция) [6; 7].

Наиболее простым и распространенным подходом является пространственная декомпозиция, при которой по вычислительным узлам распределяются данные [1]. При этом программа обработки одинакова для всех потоков.

В работе С.Б. Попова [4] показано, что основные затраты на обработку изображений связаны с низкоуровневыми операциями, выполняющими преобразования над всеми

30 Выпуск 1/2019

точками изображения и формирующими либо измененное изображение, либо некую векторную структуру или скалярную величину. Эти операции требуют значительной вычислительной мощности и ресурсов хранения. Время выполнения задачи в целом определяется в большинстве случаев именно временем, затрачиваемым на выполнение низкоуровневых операций.

Наиболее популярным вариантом организации вычислений при распараллеливании низкоуровневых операций на основе декомпозиции по данным является использование программы-менеджера в сочетании с централизованным хранением обрабатываемых изображений. В задачи специальной программы-менеджера входит считывание данных с устройства хранения, распределение данных по потокам (операция Split), ожидание завершения обработки, получение результатов от всех потоков (операция Join) и сохранение результатов обработки на устройстве долговременного хранения [12].

В качестве демонстрации расчета оперативности параллельной обработки изображений на основе предложенной модели приведем пример с использованием условных данных работы системы. На рисунке 3 изображена соответствующая СеМО, содержащая три узла типа Split-Join, с равновероятным выбором каждого из узлов (вероятности p ₁, p ₂, p ₃).

Рис. 3. Пример модели распределенной обработки изображений

Зададим интенсивность поступления заявок в СеМО λ = 4,0. В таблице 1 приведены условные параметры процесса обработки изображений.

Таблица 1

Условные параметры процесса обработки изображений

Начальные моменты распределения длительности обработки в узлах	Узлы СеМО
	S1	S2.1	S2.2	S2.3	S3
f 1	0,50	0,80	0,70	0,90	0,40
f 2	1,20	3,12	2,20	4,20	0,80
f 3	12,00	44,00	34,00	84,00	3,20

Для дальнейшего расчета сети используем аппроксимацию распределений длительности обслуживания узлов гиперэкспоненциальным распределением второго порядка (H2) по методу моментов [5]. В таблице 2 приведены параметры аппроксимирующего H2 распределения для узлов сети, расчет произведен по данным таблицы 1.

Хабаров Р.С., Лохвицкий В.А. Модель оценивания оперативности многопоточной...   31

Таблица 2

Параметры аппроксимирующего гиперэкспоненциального распределения для распределения длительности обслуживания узлов СеМО

Узлы СеМО	Параметры аппроксимирующего H2 распределения
	y	μ 1	μ 2
S1	0,0220	0,2249	2,4313
S2.1	0,0330	0,1669	1,6057
S2.2	0,0133	0,1348	1,6415
S2.3	0,0210	0,1156	1,3631
S3	0,0777	0,5451	2,5799

В таблице 3 указаны рассчитанные по формуле (2) моменты обслуживания в узле S2.1 при различных значениях числа каналов. Очевидно, что с увеличением количества каналов среднее время обслуживания уменьшается. Однако особенность дисциплины обслуживания Split-Join оказывает значительное влияние на время обслуживания Так, при увеличении количества каналов до 10 среднее время обслуживания уменьшается лишь примерно вдвое, а при количестве каналов, равном 100, – в 8 раз.

Таблица 3

Моменты распределения времени обслуживания для узла S2.1 (Split-Join) от числа каналов

Количество каналов обслуживания	Моменты обслуживания			Дисперсия	Коэффициент вариации
	f 1	f 2	f 3
1	0,80	3,12	44,00	2,44	1,95
2	0,63	1,50	10,94	1,09	1,64
5	0,47	0,55	1,72	0,34	1,25
7	0,42	0,40	0,87	0,22	1,10
10	0,37	0,28	0,43	0,14	1,02
15	0,28	0,18	0,19	0,10	1,12
20	0,22	0,12	0,11	0,07	1,24
30	0,17	0,07	0,04	0,04	1,24
50	0,15	0,04	0,01	0,02	1,02
100	0,10	0,030	0,01	0,02	1,33

На основании данных таблиц 1–3 зададим параметры СеМО. Будем считать, что узлы S1 и S3 содержат три канала обслуживания (M/H2/3).

Расчет СеМО позволяет определить моменты времени пребывания заявки в сети, по которым можно построить соответствующую ДФР, представляющую вероятностью того что полная обработка заявки завершится в заданный интервал времени.

На рисунке 4 представлены графики ДФР при различном числе каналов в узлах S2.1, S2.2, S2.3 и интенсивности входного потока λ = 4,0. Видно, что увеличение числа каналов приводит к значительному сокращению времени пребывания заявки в сети (времени

Выпуск 1/2019

полной обработки изображения). На рисунке 5 представлены графики ДФР при различных значениях интенсивности входящего потока. Число каналов каждого из узлов S2.1, S2.2, S2.3 выбиралось равным двум ( n = 2).

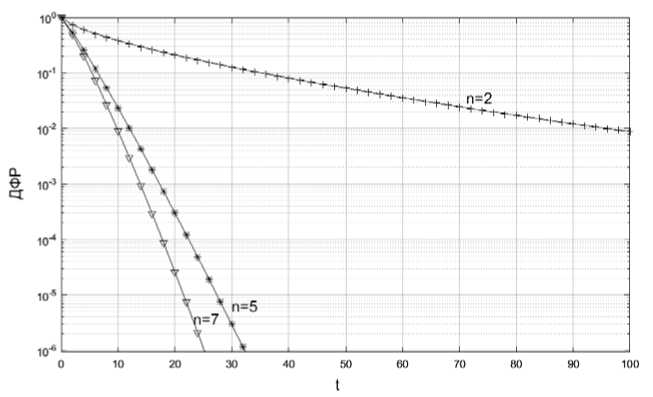
Рис. 4. ДФР времени пребывания заявки в СеМО (времени полной обработки) для различного числа каналов в узлах S2.1, S2.2 и S2.3

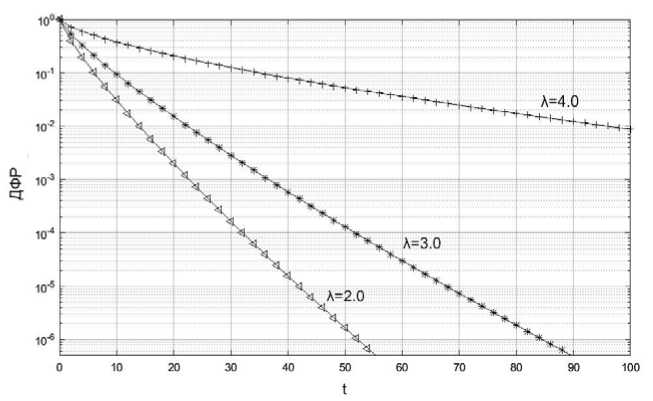
Рис. 5. ДФР времени пребывания заявки в СеМО (времени полной обработки) при различных интенсивностях входного потока

Заключение

Предложенная модель позволяет получить оценки оперативности параллельной обработки задач в виде моментов времени обработки задачи и соответствующей ДФР представляющей собой вероятность непревышения времени обработки заданного

Хабаров Р.С., Лохвицкий В.А. Модель оценивания оперативности многопоточной... 33

интервала. Выполненная оценка оперативности позволяет выявить влияние различных значений интенсивности поступления задач, быстродействия узлов обработки и количества параллельных потоков обработки на время получения целевой информации и сделать вывод о возможности многопоточной обработки требуемых объемов задач в заданных условиях.