Модель оценки влияния испарения диспергированной жидкости на теплофизические параметры продуктов сгорания ракетной камеры

Тел. (846) 267-45-73

Тел. (846) 267-45-73

кости, а на сужающемся участке сопла (0-1) разгон образовавшихся капель до скорости ω _ikp . В сечении “0” известны параметры частиц: диаметр d_{i 0} , плотность вещества ρ _{i 0} , расход жидкости m & _ж , также известны все термодинамические параметры потока продуктов сгорания: вязкость η_α , давление p_к , температура T _α , плотность ρ_{α 0} , расход m & _α (рис.1).

При формировании модели были использованы следующие допущения:

• 1.    Диспергирование жидкости происходит сразу за срезом капилляра, причём поток капель жидкости считаем монодисперсным а капли сферическими.

• 2.    В минимальном сечении сопла газообразная часть рабочего тела всегда достигает скорости звука.

• 3.    Скорость движения диспергированной фазы в минимальном сечении сопла определяется её взаимодействием на участке (0-1) (рис.1).

• 4.    При расчёте времени прохождения каплей участка (0-1) (рис.1) и определении скорости капли в минимальном сечении сопла испарение жидкости не учитывается.

• 5.    При диспергировании температура жидко-

• Рис. 1. Движение капли на дозвуковом участке 0-1

сти не меняется, теплообмен происходит только с поверхностным слоем капли, без изменения температуры неиспарившейся части капли.

На рис. 1 приняты следующие обозначения: 1 - капилляр; 2 - жидкость; 3 - сопло; —_{а вх} -скорость продуктов сгорания, в месте выхода жидкости из капилляра; — ж - скорость жидкости на выходе из капилляра; ®_а кр - скорость продуктов сгорания в минимальном сечении сопла; — _ikp - скорость капель жидкости в минимальном сечении сопла; Д х - расстояние от сечения 0 до сечения 1; Д Q _a - энергия, подводимая к единичной капле.

Модель расчёта временных и скоростных параметров движения капель жидкости предложена в статье [3], в ней получено аналитическое решение уравнения движения капель, основанное на воздействии на капли доминирующей аэродинамической силы и достижении в минимальном сечении сопла газовой частью потока скорости звука.

Так, скорость, которую приобретет капля жидкости, пройдя путь от места ввода (сечение 0), до минимального сечения (сечение 1), определяется уравнением:

й), ikp

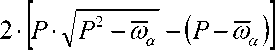
_п 1 L — Ai -Дх I где- P = - -1 k + — + —----I • где:                                    ;

• —   ^— а вх ^{+ —} a kр

• — _а =----2----- средняя скорость про

дуктов сгорания на участке (0-1);

k – коэффициент расширения продуктов сгорания на участке (0-1);

0,5     0,5

Д — ^1 • г _ ³ ^ * ^П а ^{Р а} 0

Ai        ^ = 4* О ; ^i= 13 ’ di 0        4        pi а время Дтi, в течение которого капля жидкости переместится из сечения “0” в сечение “1” (рис. 1), уравнением:

д Q a ( 0 - 1 ) = а * - F - T - T s ⁽ P k )) -Д т„ (3) где а * - коэффициент теплопередачи, Вт/м² К;

F_i0 = п - d ' ₀ - площадь поверхности капли в 0-м сечении, м²;

d_{i 0} – диаметр капли жидкости в 0-м сечении, м;

Т _а = Ф р - Т_k - температура продуктов сгорания в камере, К;

Тk – теоретическая температура продуктов сгорания в камере, К;

ф р - полнота расходного комплекса;

T s ( P_k ) - температура насыщения воды в зависимости от давления, К;

д T i - время прохождения капли от места ввода через капилляр до минимального сечения сопла, с.

Для определения коэффициента теплопередачи, от продуктов сгорания к капле жидкости, можно использовать зависимость Ренца-Марша-ла [4], которая для водяного пара, с учётом небольшой нестационарности, принимает вид:

Nu = 2 + 0,56 - VRe .         (4)

где Re = ^Р ‘ ⁰ ^' 0 ^Юа ——— - число Рейнольдса;

П а

П_а - вязкость продуктов сгорания, Па ^. с;

_ _ Д х

• ^— ' = Дт - средняя скорость диспергированной жидкости на участке (0-1), м/с;

*

_ ^а - ^di 0

Nu = ^ -число Нуссельта;

^ см -коэффициент теплопроводности среды, Вт/мК.

Энергия Д Q _a ( _{0 - 1} ) идёт на нагрев и испарение только поверхностного слоя массой Д m i каждой капли:

B i

Л       Д Q a ( 0 - 1 )

Д m,. =-----—- • i         Bi     ;

= ci-⁽T_s ⁽ P k ^)- T 0 ⁾⁺ r ⁽ P k ) ,

^{2 -( k -} ^^ ^Дт ' =   .,

^— ikp )

’а - ^— ikp

.

Формулы (1) и (2) используем при расчёте влияния испарившейся части жидкости на теплофизические параметры продуктов сгорания. Проанализируем теплообмен движущейся капли на участке движения (0-1). К капле за время Д T i от окружающего высокотемпературного газа подводится энергия Д Q _{a (0 - 1)} .

где: с _i – средняя изобарная теплоёмкость жидкости, Дж/кгК;

T ₀ – начальная температура жидкости, К;

r ( p_k ) - удельная теплота испарения, Дж/кг.

Тогда масса каждой капли в минимальном сечении сопла составит:

m i1 = m '0 ^-Д m i ,            ⁽⁷⁾

где m i ₀ = p _i0 - V i ₀ - масса капли жидкости после ввода через капилляр, кг;

p _i0 - плотность жидкости, кг/м³;

Vi0 – объём капли, м3, а диаметр капли в минимальном сечении сопла, сечение 1:

Mt =

d_{i 1}

3 ⁶ • m l

NⁿP ii ^.

q •

^ 1    1 - q

— +--

< m,    q

Ma )

Причём на участке (0-1) одновременно находятся капли общей массой M_i :

M, = fi ‘At.              (9)

iжi

Тогда количество капель N_i на этом участке составит:

M

N i = —^L m i 0

.

Таким образом, можно определить массу испарившейся жидкости, на участке (0-1):

A M , = N i -A m i .           (11)

и её относительное количество:

A Mi =

A M , M i

Рассмотрим влияние испарившейся части балласта на теплофизические параметры продуктов сгорания. Определим коэффициент балластирования, как отношение массового расхода испарившейся жидкости к сумме массового расхода топлива и балласта:

где m , , M_a — молярная масса жидкости и продуктов сгорания, кг/кмоль;

Расчёт испарения капли состоит из ряда итераций (j). Где рассматривается движение капли жидкости от выхода из капилляра до критического сечения сопла. Скорость движения продуктов сгорания на участке (0-1), в первой итерации определяется как среднее значение скорости в сечениях 0 и 1. В первой итерации не учитывается влияние испарившейся части жидкости на скорость и температуру в камере. Учёт этого влияния производится в последующих итерациях. Необходимо отметить, что значение температуры в камере сгорания Т _а остаётся неизменным. Во всех итерациях, производится последовательное изменение термодинамических параметров продуктов сгорания:

скорости to a tpj :

I 21 Rm toatpj=^k+1 • Mt; Т kj,          (16)

q

m исп

ma

+ m ucn

где: Rм – универсальная газовая постоянная, Дж/ кмольК;

молярной массы M _t j (15), температуры торможения T_kj (14), давления в камере сгорания р_кj :

где: fl_a - массовый расход топлива, кг/с;

p kj

= ptj-1 •

т исп

AM i – массовый расход испарившей-At,

*

^{1 q} j -1 I T tj   ^M tj - 1

----------------------------- .        -----------------------------------

*

^{1 — q} j     N ^T tj - 1 ‘ ^M tj

плотности p_a j :

ся части балласта, кг/с.

Используя уравнение сохранения энергии, определим температуру торможения смеси продуктов сгорания и испарившейся части в камере:

^-^ • c p a • ^T _a + c pn • T s ( p_t ^)— r ( p_t ^)— C I • ( T s ( P k ^)— T B, )

*q

^k                h q ._ ₊_                ,(14)

c p a ⁺ c pn

q

_ P j- M tj

^Paj R ,T * . ⁽¹⁸⁾ R M T tj

Для определения ® _itp и At , . значения (16) и (18) подставляем в уравнения (1) и (2). Дальнейший расчёт ведётся по выше описанной методике.

В каждой итерации оценивается изменение Т_k ^* _n . Расчёт завершается на j – итерации при относительном изменении температуры:

где: c_{p a} , c_pn — средняя изобарная теплоёмкость продуктов сгорания и насыщенного пара, Дж/кгК;

c_i – средняя теплоёмкость жидкости, Дж/кгК;

Т_вх – температура жидкости на выходе из капилляра, К.

Наличие балласта в камере сгорания приводит к изменению работоспособности рабочего тела за счёт изменения, как его температуры, так и состава. Молярную массу рабочего тела M _t , после испарения жидкости можно определить как:

Т — T _e , = _Л---^tj-L <  0,01 .

Тk ^* j

T tj — 1

Таким образом, предложенная модель позволяет определить количество испарившегося балласта, а также влияние испарившейся части жидкости на работоспособность рабочего тела камеры сгорания, а значит и огнетушащую способность аэрозоля.