Модель оценки влияния корреляционной зависимости погрешностей координат на точность определения относительной позиции при совместном маневрировании кораблей

Постановка проблемы

В настоящий момент спутниковые навигационные системы (СНС) являются основным средством для обеспечения навигационной безопасности плавания. Использование АИС на основе СНС в режиме высокой точности (дифференциальном режиме) позволяет найти относительные координаты корабля с высокой точностью. Определение относительных координат при работе СНС в стандартном режиме характеризуется значительной погрешностью и не позволяет обеспечить решение задач совместного маневрирования.

Результаты исследования

Использование автоматизированной информационной системы (АИС) для предупреждения столкновений кораблей в качестве оборудования, дополняющего радиолокационную станцию (РЛС), стало возможным благодаря автоматизации обмена информацией между судами и кораблями о местоположении и параметрах движения оцениваемых объектов, выработанных с применением спутниковых навигационных систем (СНС) ГЛОНАСС и GPS NAVSTAR и позволило в значительной степени повысить точность расчета параметров сближения [1-3].

В большинстве работ [2-4] анализ использования АИС для оценки опасности столкновения оценивался по работе СНС ГЛОНАСС и GPS NAVSTAR в дифференциальном режиме (погрешности определения местоположения 5-10 м [5]), когда фактические поправки на условия распространения радиоволн определяются в специально оборудованной точке и используются в реальном масштабе времени на кораблях, находящихся в зоне действия этих поправок [5].

Реализация дифференциального режима навигационных определений возможна при приеме и обработке сигналов спутниковой радионавигационной системы в двух разнесенных точках ее рабочей зоны:

• –    точке нахождения определяющего координаты корабля;

• –    точке расположения береговой аппаратуры, обеспечивающей формирование корректирующей информации для уточнения координат определяющегося корабля.

Основное использование СНС ГЛОНАСС и GPS NAVSTAR характеризуется работой в стандартном режиме (погрешности определения местоположения 40 м [5]) и обеспечивается:

• –    тропосферной поправкой (рассчитывается по модели в зависимости от текущей угловой высоты спутника для параметров стандартной атмосферы);

• –    ионосферной поправкой (рассчитывается по модели, для которой используются параметры, передаваемые в составе навигационного сообщения).

Оценить характер погрешностей СНС ГЛОНАСС и GPS NAVSTAR позволили исследования, проводимые во время опытной и штатной эксплуатации в различных районах Мирового океана. В результате обработки статистических данных были получены нормированные временные автокорреляционные функции (АКФ) погрешностей навигационных параметров (НП) [6], которые используем для оценки влияния корреляционной зависимости погрешностей определения координат с применением СНС ГЛОНАСС и GPS NAVSTAR на точность определения относительной позиции при совместном маневрировании кораблей.

Для упрощения расчетов этого введем прямоугольную систему координат Х0Y, начало которой совпадает с местом объекта маневра (уравнителя) М с координатами (X 0 =0,Y₀=0), 0Y имеет направление на восток, а 0X - на север. Маневрирующий корабль К имеет координаты (X₁,Y₁); назначенная маневрирующему кораблю К позиция относительно объекта маневра (уравнителя) М имеет координаты (X_H,Y_H). Координаты объекта маневра (уравнителя) М, маневрирующего корабля К известны с точностями, равными ожидаемым РСКП объекта маневра (уравнителя) М М М иманеврирующего корабля К М К соответственно (рис. 1).

Расчет элементов относительной позиции ( П _Ф и D _Ф) с учетом случайных погрешностей координат маневрирующего корабля К, корреляционно зависимых с случайными погрешностями координат объекта маневра (уравнителя) М, основан на теореме предсказания [7], в соответствии с которой можно предсказать значение случайной величины x(t+ τ ) в момент времени (t+ т ), если известны ее текущее значение x(t), автокорреляционная функция рх( т ) и вспомогательная случайная величина у(t), некоррелированная с x(t), с нулевым математическим ожиданием и со СКО σ, равным СКО случайной величины х(t) σ х, т. е. _

x ( t ^{+ т )} = Р x ^{( Т} ) • x ( t ) ⁺ V¹ - Р ^{2 ( Т )} • У ⁽ t )•                                   ⁽¹⁾

Следовательно, на один и тот же момент времени (шаг моделирования) можно предсказать значение случайной величины АХ 1 , если известно значение другой случайной величины АХ 0

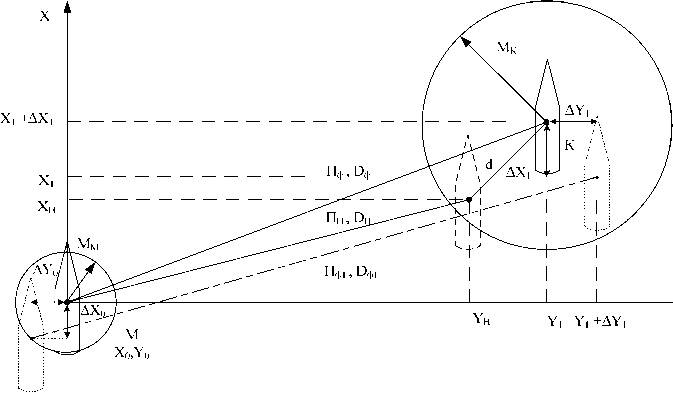
Рис. 1. Позиции совместно маневрирующих кораблей, определяемые случайными погрешностями координат

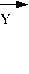
коэффициент корреляции между ними r и значение вспомогательной случайной величины АХ_пЬ некоррелированной с АХ ! [7],

^X 1 = r_x " A X о + -J 1 - r^ " A X п i .

Для получения корреляционно зависимых случайных погрешностей координат маневрирующего корабля К и объекта маневра (уравнителя) М рассчитываются коэффициенты:

^а1 - о 1^ 1 ^- r i ;                                                                  (3)

b 1 - r ,                                                                                    (4)

где О ] - СКО случайной погрешности координат маневрирующего корабля К;г - коэффициент корреляции случайных погрешностей координат маневрирующего корабля К и объекта манев-ра(уравнителя)М.

Случайные погрешности координат маневрирующего корабля К, корреляционно зависимые с случайными погрешностями координат объекта маневра (уравнителя) М, будут определяться так:

А ^X 1     A ^X 0 • ^Ь 1 ⁺ A ^X П 1 • а 1 ;

A Y1 - A Y0 • bx +А Yn 1 • а,, где АХП1, АУП1 - вспомогательные случайные величины, не коррелированные с случайными погрешностями координат объекта маневра (уравнителя) MAX0, AY0 и распределенные по нормальному закону распределения с математическим ожиданием, равным нулю, и со СКО, соответствующим РСКП места маневрирующего корабля К.

Моделирование корреляционно независимых случайных погрешностей координат совместно маневрирующих кораблей произведено с использованием стандартной функции про- граммной среды Mathсad (rnorm(N,mu,sigma)) [7], выдающей N случайных чисел, распределенных по нормальному закону распределения, с математическим ожиданием mu и СКО sigma. Математическое ожидание mu принято равным нулю, СКО sigma - РСКП координат маневрирующего корабля К о К = -К- и РСКП координат объекта маневра (уравнителя)

ММ

М о М

Расчет элементов относительной позиции совместно маневрирующих кораблей производится по формулам пф = arctg

( Y + А Yb + А Y_nа, ) - ( Y + А Y _o)

1         0 1 П1 1         00

—

( X 1 + А X 0 b + АX _п 1 а 1 ) - ( X о + А X о )

D ф = V [ ( X 1 +А Х о b , +А Х п 1 а , )-( X о +А Х о ) ] ² + [ ( Y ; +А Y о b , +А Y п 1 а , )-( Y _o +А Y о ) ] ² . (8)

Математическая модель корреляционной зависимости случайных погрешностей координат, выработанных с использованием СНС ГЛОНАСС и СНС NASTAR GPS, определяется формулами (9) и (10) соответственно:

р(Ат) = е'; (9)р (Ат) = е, (10)

где Δ τ - разность во времени снятия отсчетов корабельных приемоиндикаторов (КПИ) СНС совместно маневрирующих кораблей, в секундах. В данном случае рассматриваем выполнение обсервации совместно маневрирующими кораблями по одному созвездию навигационных космических аппаратов [8]. Разность времени снятия отсчетов КПИ СНС примем равной 1, 4 и 12 с. Данный интервал времени определяется дискретностью выдачи динамической информации аппаратурой АИС [9]. Также допускаем, что координаты мест совместно маневрирующих кораблей приведены на один момент времени.

Оценка влияния корреляционной зависимости случайных погрешностей координат совместно маневрирующих кораблей на точность определения относительной позиции производилась методом имитационного моделирования и определялась по значению отклонения от назначенной позиции по формуле d = VDH + D« - 2DHDo cos АП . (11)

Исследования, проведенные с использованием разработанной модели, показали, что при разности во времени снятия отсчетов КПИ СНС ГЛОНАСС, равной 1, 4 и 12 с, случайная погрешность определения относительной позиции составила 4,8, 9,6, 16,2 м соответственно, а при использовании СНС NASTAR GPS - 5,3, 10,5, 17,6 м соответственно (рис. 2). При этом учитывалось выполнение обсерваций на совместно маневрирующих кораблях по одному созвездию НКА [8].

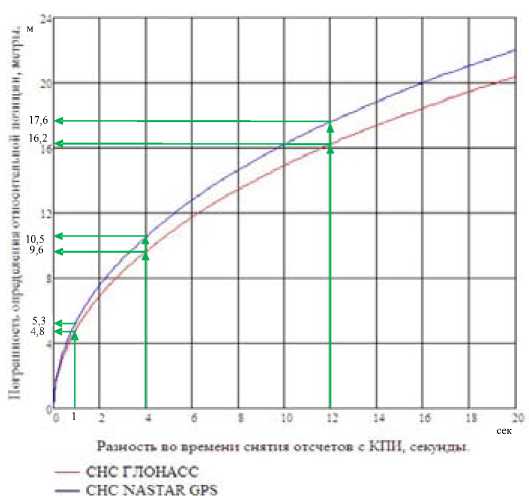
Рис. 2. Случайная погрешность относительной позиции совместно маневрирующих кораблей при разности времени снятия отсчета 1, 4 и 12 с

Таблица 1. Абсолютное и относительное уменьшение случайной погрешности относительной позиции совместно маневрирующих кораблей при разности времени снятия отсчета по СНС ГЛОНАСС и СНС NASTAR GPS 1, 4 и 12 с

СНС Δτ, с	1	4	12
	Абсолютное уменьшение случайной погрешности относительной позиции, разы
СНС ГЛОНАСС	8,2	4,1	2,5
СНС NASTAR GPS	7,5	3,8	2,3
Относительное уменьшение случайной погрешности относительной позиции, %
СНС ГЛОНАСС	88	75,8	60
СНС NASTAR GPS	86	73,6	55,9

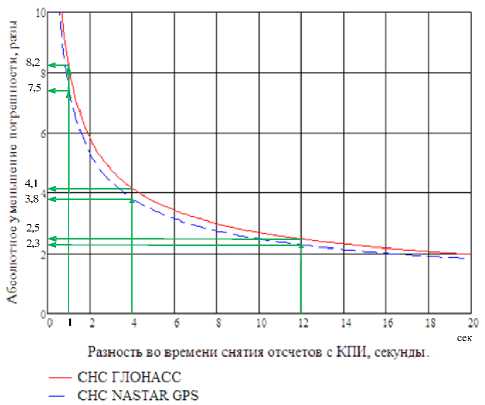
Рис. 3. Абсолютное уменьшение случайной погрешности относительной позиции совместно маневрирующих кораблей при разности времени снятия отсчета по СНС ГЛОНАСС и СНС NASTAR GPS 1, 4 и 12 с

Абсолютное и относительное уменьшение случайной погрешности относительной позиции, определяемой по координатам совместно маневрирующих кораблей, выработанных в стандартном режиме и по одному созвездию НКА СНС ГЛОНАСС и СНС NASTAR GPS с разностью времени снятия отсчета 1, 4 и 12 с, представлено в табл. 1 и на рис. 3, 4.

Вывод

Полученные значения случайных погрешностей определения относительной позиции соизмеримы с использованием СНС ГЛОНАСС и СНС NASTAR GPS в дифференциальном режиме навигационных определений и значительно превосходят по точности используемые для определения относительной позиции совместно маневрирующих кораблей РЛС и систему автоматической радиолокационной прокладки (САРП).

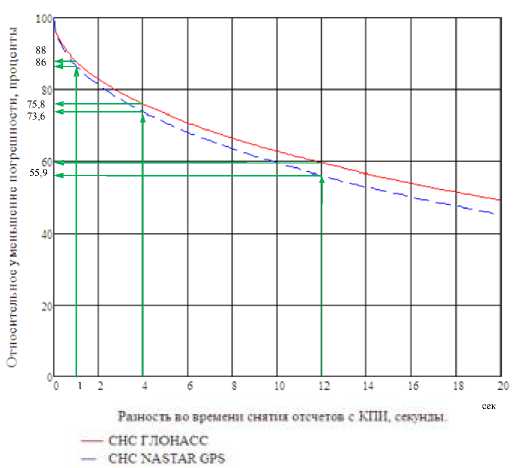
Рис. 4. Относительное уменьшение случайной погрешности относительной позиции совместно маневрирующих кораблей при разности времени снятия отсчета по СНС ГЛОНАСС и СНС NASTAR GPS 1, 4 и 12 с