Модель однокристального вычислителя для подавления реверберационных помех

Широкая область использования приборов обработки низкочастотных сигналов, от бытовых звуковоспроизводящих устройств до профессионального медицинского и научно-исследовательского оборудования обуславливает необходимость создания эффективных систем подавления реверберационных помех [1] . В данном случае под эффективностью понимают обеспечение гашения прямого и остаточного эхо-сигнала в режиме реального времени с заданным качеством и минимальными вычислительными затратами [2] . Повышение качества подавления основной помехи обеспечивается использованием различного рода схемами и алгоритмами подавления [3 –5] . В свою очередь для борьбы с остаточным эхом авторами предложено использовать технологии машинного обучения [6, 7] . Однако обеспечение функционирования фильтра в режиме реального времени, то есть выполнение всех вычислительных операций в заданном временном диапазоне является сложной инженерной задачей. Решение может быть получено при использовании специализированных вычислителей, реализованных на основе сверхбольших интегральных схем, например в базисе ПЛИС (программируемая логическая интегральная схема). Распараллеливание информационных потоков на ПЛИС и реализация основных математических операций с помощью встроенных блоков цифровой обработки сигналов (DSP) позволит решить поставленную задачу. Однако для реализации нейронной сети на ПЛИС требуется выбор типа (класса) сети, наиболее полно отвечающего поставленным задачам, разработка архитектуры, построение модели сети, ее обучение и создание сложно-функциональных блоков для генерации ПЛИС – проекта в составе однокристального вычислителя подавления реверберационных помех.

Известные решения в проблемной области

Известно, что наилучшие результаты при подавлении эха получают с помощью методов адаптивной фильтрации. При таком подходе на основе опорного сигнала, как источника эха, вычисляется сигнал коррекции. Известен ряд наиболее распространённых алгоритмов адаптивного подавления. Например, алгоритм наименьших квадратов (LMS), нормализованный алгоритм наименьших квадратов (NLMS), блочный алгоритм наименьших квадратов (BLMS) и другие [5 , 8, 9, 12] .

Однако, применение алгоритмов адаптивной фильтрации имеет ряд недостатков. Например, известные алгоритмы имеют ненулевое время сходимости, в течение которого сигнал может заметно искажаться. Также после применения алгоритмов адаптивной фильтрации сигнал зачастую содержит остаточное эхо.

Для устранения негативных последствий фильтрации применяют подходы к подавлению на основе гибридных систем [10, 18] . С одной стороны такой подход при моделировании показывает хорошие результаты. С другой, при практической реализации эффективная имплементация этих архитектур на интегральной схеме будет вызывать затруднение, поскольку количество и разрядность используемых нейронов требует значительных вычислительных затрат и памяти для размещения. Отметим, что наиболее ресурсозатратным модулем системы шумоподавления, является модуль вычисления кепстральных коэффициентов.

Учитывая известные достижения в области реализации нейронных сетей в базисе сверхбольших интегральных схем [10, 11] , можно сделать обоснованное предположение о том, что рекуррентная нейронная сеть применительно к задаче вычисления кепстральных коэффициентов для подавления остаточного эха может быть реализована как целочисленная сеть эхо-состояний (ESN) с меньшими вычислительными затратами и значительно меньшим объемом памяти. Такой подход позволит обеспечить повышение эффективности реализации однокристального вычислителя для подавления реверберационных помех.

Таким образом, задача создания однокристального вычислителя для подавления реверберационных помех может иметь решение при использовании комбинированного подхода, а именно – реализация адаптивного алгоритма и целочисленной сети эхо-состояний в базисе ПЛИС. Следовательно, актуальной является задача построения полнофункциональной модели вычислителя для ее последующей трансформации в базис ПЛИС и натурной отработки.

Предлагаемое решение

На рисунке 1 представлена структурная схема предлагаемого решения. В состав однокристального вычислителя входят: двухканальный приёмник аналогового аудиосигнала, принимающий входной сигнал с микрофона (Mic-End) и эхо-сигнал «с дальнего конца» (Far-end), обрабатываемые посредством аналого-цифрового преобразователя (АЦП). Также в состав вычислителя входят: модуль вычисления признаков сигнала, адаптивный фильтр фильтрации в частотной области (например FDAF), модуль быстрого преобразования Фурье БДПФ, нейросеть (НС), слой для перемножения полученных от НС коэффициентов со спектром сигнала (Х), модуль для вычисления обратного преобразования Фурье (ОДПФ) и цифро-аналоговый преобразователь (ЦАП).

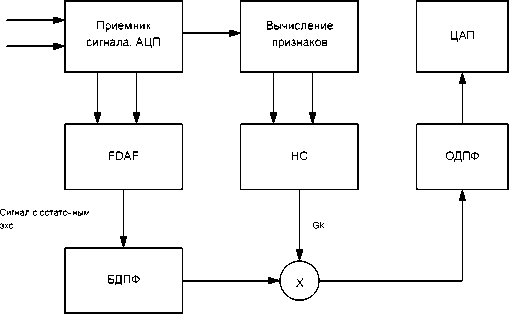
Рисунок 1. Предлагаемая структура однокристального вычислителя для подавления реверберационных помех

Сигнал с микрофона Mic-end и сигнал «дальнего конца» Far-end поступают на приемник аналогового сигнала и проходят аналоговоцифровое преобразование. Далее цифровые сигналы передаются в модуль подавления эха, функционирующий на основе алгоритма адаптивной фильтрации, который позволяет адаптировать коэффициенты фильтра в зависимости от изменяющихся условий сигнала в частотной области. В результате работы адаптивного фильтра, выполняется подавление основного эха. При этом в выходном сигнале, как правило, присутствует остаточное эхо.

На следующем этапе используется предварительно обученная нейрон ная сеть, которая позволяет компенсировать остаточный эхо-сигнал. На рекуррентную нейронную сети покадрово поступают признаки, рассчитываемые для сигнала Far-end и микрофонного сигнала Mic-end. На выходе нейронной сети формируются коэффициенты предсказания значений G k для подавления остаточного эхо-сигнала путем изменения соответствующих полос его частотного диапазона.

Далее для сигнала, прошедшего этап подавления эха с помощью адаптивного фильтра и содержащего остаточное эхо выполняется вычисление спектра с помощью алгоритма быстрого преобразования Фурье.

Полученный спектр проходит разбивку на 22 частотных диапазона, соответствующих шкале Барка, которые корректируются на коэффициенты G k .

Поскольку нейронная сеть вычисляет коэффициенты усиления не для определенных частот, а для отдельных диапазонов спектра, то используется функция интерполяции:

mm

• (1)                g k ( m ) = ^ - M)g k + M^ k+i ,

где g k ( m ) — коэффициент усиления m-й частоты для k-й полосы, g ^ и g k+i — коэффициенты усиления для k -й и ( к + 1)-й полос, а M обозначает ширину k -й полосы.

Далее над обработанным таким образом спектром производится операция обратного преобразования Фурье, результатом которой является сигнал во временной области с измененным частотным диапазоном остаточного эха.

Полученные результаты

Предложенный план экспериментальных исследований включал следующие основные этапы реализации моделей вычислителя по нарастающему принципу:

• (1 )    реализация модели вычислителя на основе классических адаптивных алгоритмов для оценки эффективности подавления и демонстрации наличия остаточного эха,

• (2)    реализация модели со встроенными рекуррентными нейросетями различной архитектуры для оценки эффективности подавления остаточного эха,

• (3 )    переход от рекуррентной нейросети к сети эхо-состояний для последующей целочисленной реализации,

• (4)    переход от сети эхо-состояний к целочисленной сети эхо-состояний для результирующего сравнительного анализа полученных решений.

На первом этапе реализован ряд распространённых алгоритмов шумоподавления, показывающих наилучшие результаты согласно доступным источникам: алгоритм наименьших средних квадратов (LMS - Least Mean Square), нормализованный алгоритм наименьших квадратов (NLMS), блочный алгоритм наименьших квадратов (BLMS) и алгоритм адаптивной фильтрации в частотной области FDAF (Frequency-Domain Adaptive Filter). Рассматриваемые алгоритмы были синтезированы при помощи встроенных библиотек Matlab и протестированы на созданных наборах данных. Каждый набор представлял собой комплект аудиозаписей с различными эффектами наложения реверберационных помех [7] . Был выполнен анализ более 100 исходных фрагментов аудиофайлов, в каждом из которых делались выборки по 64 кадра.

При экспериментальной оценке качества подавления эха с применением алгоритмов адаптивной фильтрации было выявлено, что алгоритм адаптивной фильтрации в частотной области (FDAF) показывает наилучшие результаты (рисунок 2) . Однако все алгоритмы оказывают влияние на

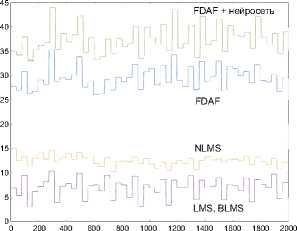
Номер аудиозаписи

( а ) средние значения

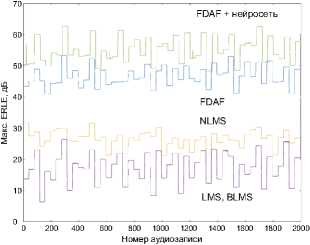
( б ) максимальные значения

Рисунок 2. Распределение значений метрики ERLE по алгоритмам

конечную амплитуду полезного сигнала «ближнего конца». Отметим, что полученные результаты не расходятся с результатами подобного тестирования других авторов [13 –17] .

Результаты моделирования на первом этапе показали, что адаптивная эхокомпенсация позволяет избавиться от линейного эха, вносимого многолучевым распространением или импульсной характеристикой (RIR) [17] . Однако из-за наличия в устройствах нелинейных компонентов, например излучателей с плохой линейностью, может возникнуть нелинейное эхо. Его нельзя устранить с помощью адаптивной фильтрации с КИХ- структурой, что приводит к остаточному эху [7, 18] . Также было определено, что амплитуда остаточного эха после адаптивной фильтрации будет меньше, чем амплитуда выходного сигнала, но такое остаточное эхо может оказывать существенное влияние на результат компенсации реверберационных помех. Поэтому остаточное эхо следует рассматривать как особый тип шума. Кроме того, этот шум может иметь связь с опорным сигналом на «дальнем конце». Следовательно, требуется подавление и этой помехи.

Для формирования признаков сигнала, позволяющих выделить факт присутствия остаточного эха и его дальнейшего подавления с помощью обученной нейронной сети, предлагается использовать метод вычисления кепстральных коэффициентов с использованием шкалы Барка [19] .

На втором этапе реализован комбинированный фильтр, включающий алгоритм адаптивной компенсации и нейронную сеть. Выбору архитектур тестируемых нейронных сетей способствовали публикации [7, 18] . Для обучения нейронной сети на ее вход последовательно подавались вектора признаков для сигнала «дальнего» и «ближнего» конца. При этом каждый вектор состоял из 24 элементов: 22 кепстральных коэффициента, а также значение энергии сигнала и значение частоты основного тона. Итого 48 входных значений на каждый кадр сигнала.

Для обучения использовалась созданная искусственная речевая база данных, которая включает 7500 синтезированных аудиозаписей фраз дикторов (по три файла на одну комбинацию фраз дикторов), база данных Microsoft AEC Challenge [20] , которая содержит более 50000 аудиозаписей дикторов в реальном окружении, а также синтезированные данные.

Для обучения нейронной сети были подготовлены следующие выборки: вектор признаков far-end (чистый референс), вектор признаков mic-end (искаженный сигнал far-end + near-end), вектор энергии полос near-end (чистая речь), вектор энергии полос после фильтра (остаточное эхо + чистая речь), отношение векторов энергий коэффициентов g _k ( G _k ).

Оценка качества обучения проводилась с помощью метрик Training loss и Validation loss. Были синтезированы нейронные сети архитектур GRU и LSTM. Общее время обучения сетей с архитектурами на основе управляемых рекуррентных блоков GRU и долгой краткосрочной памяти LSTM составило 8 часов и включало 900 эпох. Для нейронной сети на основе управляемых рекуррентных блоков GRU в результате обучения было получено итоговое значение Training Loss – 0,039. Для нейронной сети с архитектурой LSTM в результате обучения было получено итоговое значение Training Loss – 0,035.

На рисунке 2 отображено распределение средних и максимальных значений метрики ERLE для используемой выборки аудиозаписей речевых сигналов.

В таблице 1 представлены результаты сравнительного анализа для алгоритмов LMS, NLMS, BLMS, FDAF, а также комбинированного FDAF с нейросетевым модулем архитектуры LSTM. Приведены среднее и среднее-максимальное значение метрики ERLE.

Для сравнения эффективности подавления остаточного эха различными архитектурами рекуррентых нейронных сетей был проведен эксперимент, в котором в качестве нейросетевого модуля были использованы два вида нейронных сетей: управляемые рекуррентные блоки GRU и долгая краткосрочная память LSTM.

Таблица 1. Оценка качества подавления эха

Алгоритм	Среднее значение ERLE, дБ	Среднее-максимальное значение ERLE, дБ
LMS	6.98	17.26
NLMS	12.52	26.70
BLMS	6.98	17.28
FDAF	29.51	46.71
FDAF + нейросетевой модуль LSTM	37.39	55.21

Входной каскад системы, включающий блоки подавления основного эха на основе адаптивного фильтра и вычисления признаков сигналов, содержащих остаточное эхо, оставался без изменений. Далее на предварительно обученные сети поступали вычисленные признаки, а на выходах сетей формировались соответствующие коэффициенты усиления, которые использовались в модуле модификации спектра остаточного эха (рисунок 3) .

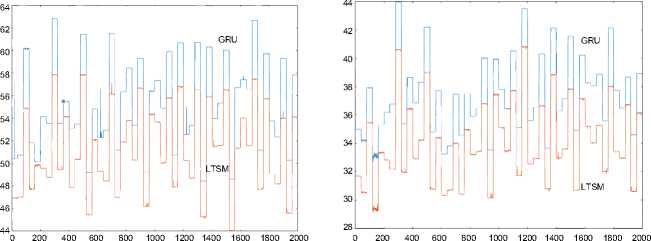
Номер аудиозаписи

Номер аудиозаписи

( а ) средние значения

( б ) максимальные значения

Рисунок 3. Распределение значений метрики ERLE для архитектур нейронных сетей

В таблице 2 приведены значения метрики ERLE для архитектур GRU и LSTM.

Из рисунка 3 и таблицы 2 видно, что для подавления остаточного эха, большей эффективностью обладает сеть на основе управляемых рекуррентных блоков GRU. Показатели ERLE в среднем выше на 3.3 дБ.

На третьем этапе экспериментов сеть на основе управляемых рекуррентных блоков GRU заменена на сеть резервуарную эхо-состояний (ESN).

Таблица 2. Оценка качества подавления эха нейронными сетями

Нейронная сеть	Среднее значение ERLE, дБ	Среднее-максимальное значение ERLE, дБ
Управляемые рекуррентные блоки GRU	37.39	55.21
Долгая краткосрочная память LSTM	34.08	51.34

Как и на предыдущем этапе входные данные для нейронной сети представляют собой конкатенацию векторов Far-end и Mic-end размерностью 24, состоящих из 22 частотных кепстральных коэффициентов с использованием шкалы Барка совместно со значениями частоты основного тона и энергией сигнала. Таким образом, вектора признаков включают по 48 элементов.

Выходные данные – это вектор из 22 вещественных коэффициентов, применяемых к соответствующим 22 барковским поддиапазонам спектра исходного сигнала. Реализованная нейронная сеть содержит 600 нейронов.

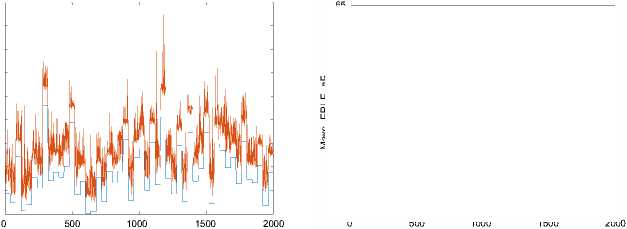
Результаты оценки качества работы нейронной сети на тестовой выборке данных в сравнении с фильтром FDAF представлены на рисунке 4 .

36 ш

Номер аудиозаписи

Номер аудиозаписи

( б ) максимальные значения

( а ) средние значения

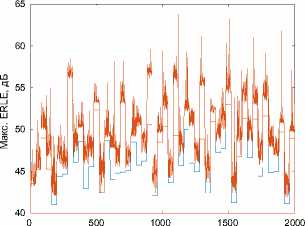
Рисунок 4. Результаты оценки ERLE на тестовой выборке (красный – ESN, синий – FDAF, больше – лучше)

Как видно по результатам тестирования, сеть эхо-состояний демонстрирует нестабильность в подавлении эха, характерны частые всплески. При этом средние показатели подавления выше.

На четвертом этапе для будущей реализации нейросети на энергоэффективном однокристальном вычислителе в модели предложено привести сеть к целочисленному варианту исполнения, сократив тем самым как разрядность операндов, так и количество используемых специализированных блоков для вычисления чисел с плавающей точкой.

Проведены эксперименты по преобразованию нейронной сети для целочисленных вычислений. Использовался инструментарий Matlab Simulink и модуль для вычислений с фиксированной точкой Fixed Point Designer.

Из рассмотренных нейросетевых архитектур была использована LSTM. Выбор обусловлен ограниченной поддержкой типов нейронных сетей. Начиная с версии R2024b в Matlab представлена функция exportNetwork-ToSimulink, позволяющая выполнить преобразование нейронной сети в модель Simulink.

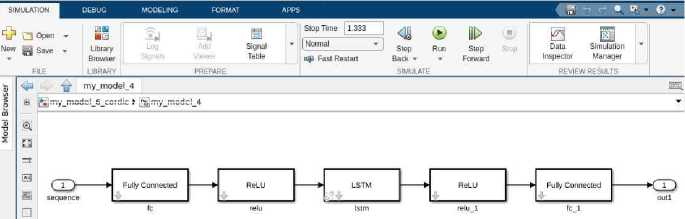
Таким образом, используя ранее обученную сеть долгой краткосрочной памяти LSTM была построена соответствующая ей модель, которая использована для среды моделирования Matlab Simulink с целью преобразования для целочисленных вычислений (рисунок 5) .

falmy model 6 cordic ► I4lmy model 4

Рисунок 5. Модель созданной нейронной сети LSTM для моделирования в среде Simulink

Посредством инструментария Matlab, в который входит Fixed-Point Tool выполнено:

• ^•    конвертация форматов данных,

• ^•    анализ ошибки округления и переполнения,

• ^•    оптимизация вычисления для систем FPGA

• ^•    предварительная генерация кода.

Fixed Point Tool предлагает два режима преобразования: автоматизированный и итеративный, с возможностью ручной модификации. Последний был использован в данном эксперименте. Алгоритм конвертации модели нейронной сети в целочисленную с помощью Fixed Point tool включал следующие основные шаги:

• (1 )    Создание резервной версии модели и ее проверка на совместимость с процессом преобразования.

• (2)    Определение диапазонов используемых данных с помощью симуляции, сбора статистики функционирования всех узлов модели.

• (3)    Определение точности (использовалась двойная точность Double precision для уменьшения эффекта квантования).

• (4)    Формирование предложений по типам данных (Propose Data Types). Вычисляются минимальные и максимальные значения, и на их основе модулем предлагаются новые целочисленные типы. Доступна возможность выборочно назначать тип данных к объектам модели (рисунок 6) .

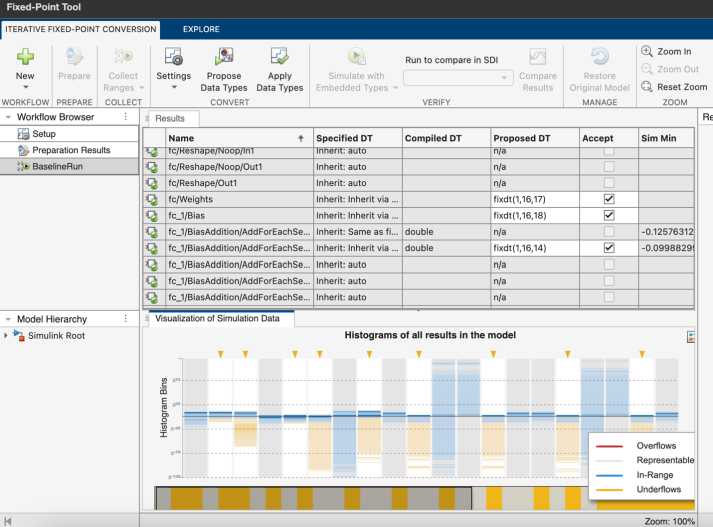
Рисунок 6. Таблица соответствия типов данных Fixed Point Tool

• (5)    Применение новых целочисленных типов данных к модели.

Таким образом с помощью Fixed Point Tool была выполнена итеративная конвертация нейронной сети LSTM в целочисленный формат. После преобразования проводилась симуляция целочисленной модели для сравнения выходных сигналов и оценки возможной потери точности посредством инструментов Compare Results (рисунок 7).

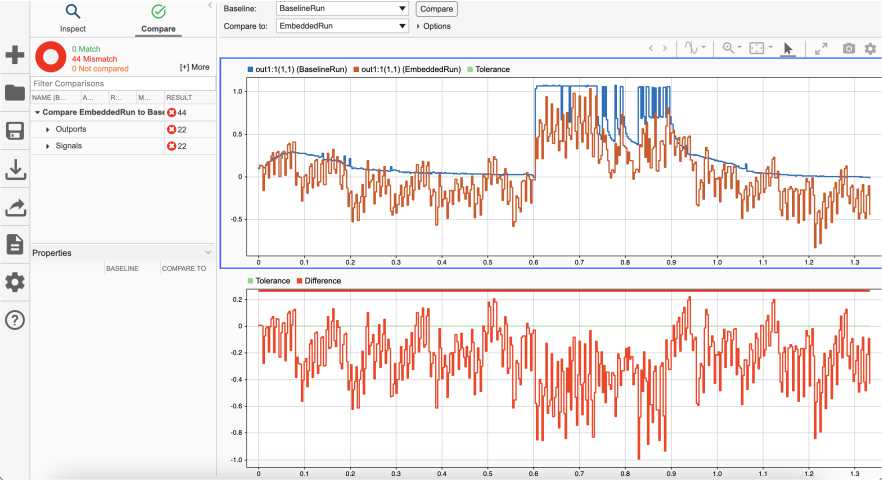
Рисунок 7. Сравнение выходных сигналов исходной (синий график) и целочисленной модели (красный график) нейронной сети

На рисунке приведены результаты сравнения выходных сигналов моделей, соответствующие 1333 входным векторам. Для симуляции работы исходной и целочисленной нейронной сети LSTM на вход моделей Simulink подавались временные последовательности с векторами признаков, состоящие из 48 коэффициентов на каждый отсчет. Из рисунка 7 видно, что полученная целочисленная модель нейронной сети выполняет адекватное формирование коэффициентов коррекции для частотных поддиапазонов спектра. При этом их значения находятся в интервалах, которые соответствуют времени присутствия остаточного эха.

Заключение

Широкий спектр задач в различных областях науки и техники при подавлении реверберационных помех, возникающих при передаче низкочастотных сигналов обуславливает актуальность данного направления исследований. Показано, что несмотря на значительные успехи при подавлении основного диапазона шумов, наличие эффекта остаточного эха следует рассматривать как отдельный вид помех, вносящих существенный вклад в искажение сигнала. Для решения данной задачи предложен комбинированный метод, основанный на использовании одного из наиболее эффективных, для конкретной задачи подавления, алгоритмов и нейронной сети. Для перехода от теоретического предположения к практической реализации создана модель однокристального вычислителя. Отличительной особенностью модели следует считать применение целочисленной сети эхо-состояний, которая позволяет не только выполнить отработку ключевых моментов предложенного подхода, снизить требования к вычислительной мощности и ресурсам, но и обеспечить перенос на различные платформы ПЛИС для практической реализации.

Таким образом, полученные результаты позволяют перейти к синтезу ПЛИС – проекта для целевого кристалла и проведению серии натурных экспериментов на действующем оборудовании.

Отметим, что при увеличении количества и разрядности используемых нейронов увеличивается точность эхоподавления. Однако при реализации сети на интегральной схеме – в виде прошивки ПЛИС, временные задержки с увеличением этих параметров будут расти незначительно ввиду параллельности производимых аппаратными блоками вычислений.