Модель одноосного растяжения идеально-пластического монокристалла

Введение В 1923-1925 годах Дж. Гейлор и К. Элам выполнили серию опытов с монокристаллами алюминия [1,2], в ходе которых было обнаружено, что процесс пластического одноосного растяжения при больших степенях удлинения сопровождается аффинными изменениями формы тела и ориентации кристаллической решетки материала в средней (удаленной от закреплений) части образца. Изучение этого простого типа экспериментов полезно для обоснованного построения определяющих соотношений поликристаллического тела, имеющих целью описать процессы, сопровождающиеся локальным поворотом решетки (фрагментацию, текстурирование). Формулируемая далее модель трактует активными все системы скольжения кристалла одновременно и в пределе сводится к модели на основе общепринятого закона Шмида [3]. Гем самым в работе исследуется адекватность применения этого закона. В качестве критерия истины используются семь измерений, сопровождающих опыт.

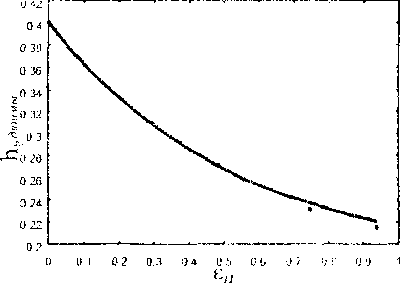
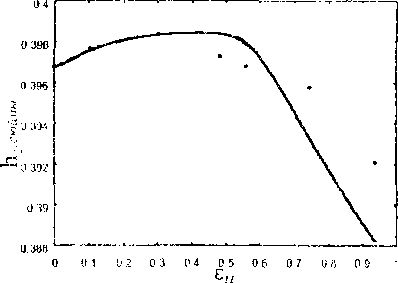
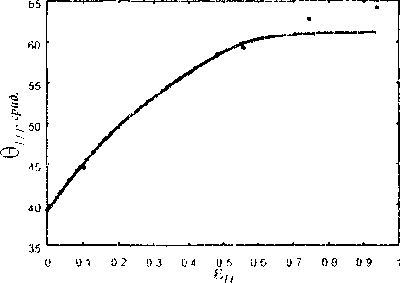
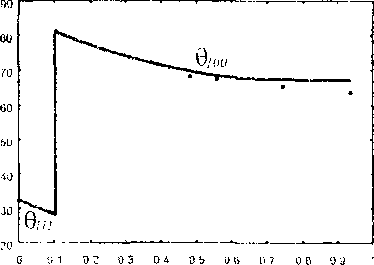
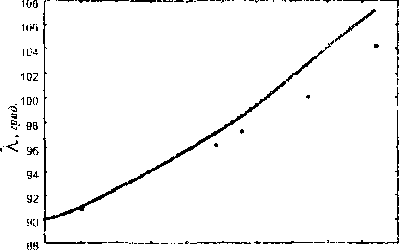
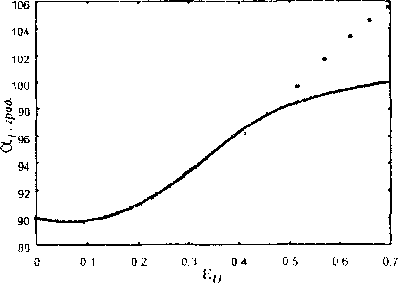
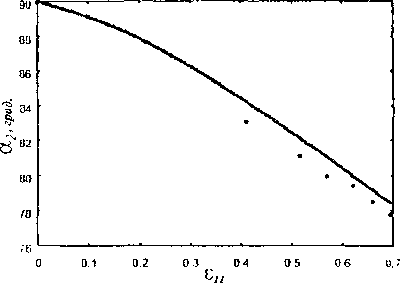
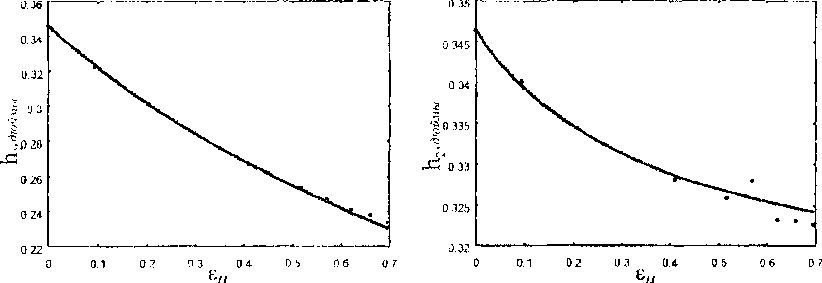
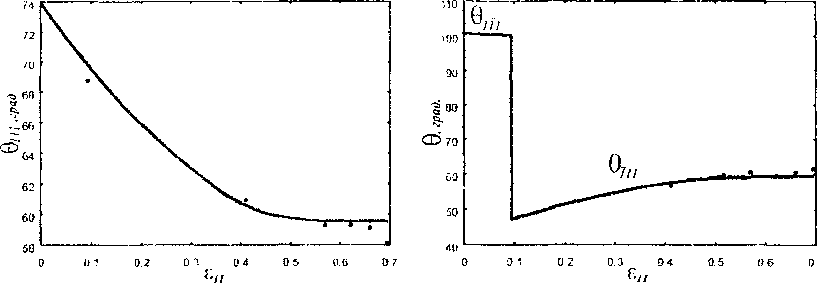
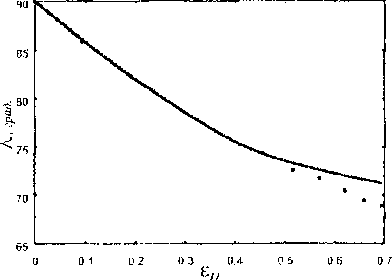
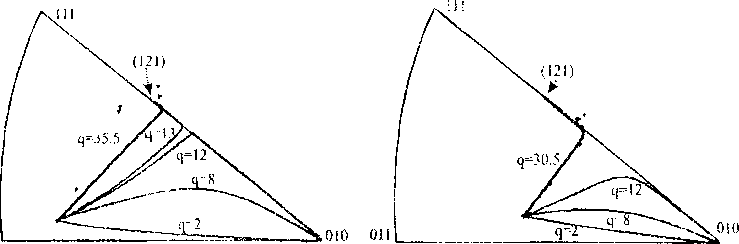
Модель Рассматривается призматический образец, подвергаемый одноосному растяжению. Материал образца -- металлический монокристалл с ГЦК-решеткой. Характер проведения эксперимента [1,2] позволяет принять для части образца, удаленной от зажимов, две гипотезы: а) об однородности напряженно-деформированного состояния, б) о параллельности образующей линии действия растягивающей нагрузки. Эта часть образца и будет рассматриваться далее. Упругими деформациями образца пренебрегают по сравнению с большими пластическими, что для металлов приемлемо. Материал считается находящимся в состоянии пластического течения и неупрочняющимся.

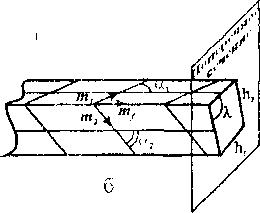
Принимается обычная гипотеза, что пластическое формоизменение монокристалла с ГЦК-решеткой осуществляется скольжением по двенадцати системам, образованным плоскостями и направлениями наиплотнейшей упаковки [3,4]. Рассмотрим сначала кинематику единичного скольжения, те. предоставим свободу движения только одной системе параллельных плоскостей с нормалью и в направлении b (|n|=|b|= 1). Данная система скольжения, произвольно ориентированная относительно приложенной силы f, под действием последней может испытывать только простой сдвиг ио плоскостям п в направлении b (рис.1)

Простой сдвиг континуума с параметром Ау вызывает изменение ориентации m ((m|=l) относительно системы нЫ (l = nxb) и длины in любого материального волокна образца:

{т;}= ™m n, m-b + m-ntg(Ay), ml},

Ф(Ду,т)

,i

Де г ™--™ = (I j.. 2(ш ■ n)(m ■ b)tg(Ay) + (m n)2 tg2(Ay))2 -1,(2)

m

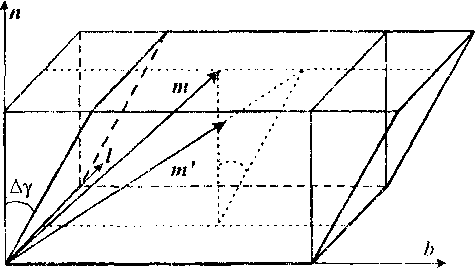
Рис. 1. Кинематика единичного скольжения где Ф(Ду, ж) и Де — соответственно кратность и деформация волокна ио Коши (Де = Ф(Дч,т) ~ 0, mi и т' — соответственно компоненты (в базисе nbl) единичного вектора т' вдоль рассматриваемого волокна и длина этого волокна после сдвига. При малом Ду формулы (1),(2) принимают вид

{dm-} = {(mn)2(mb) dy, (mn)(l-(m-b)2)dy, (m n)(m • b)(m• I) dy },(1')

de = (m • n)(m • b)dy .

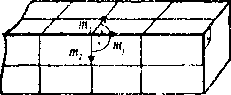
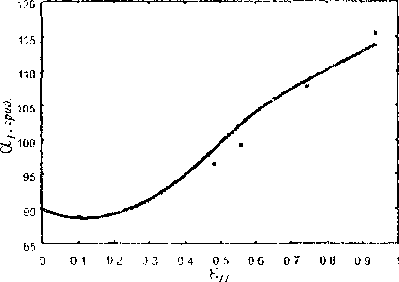
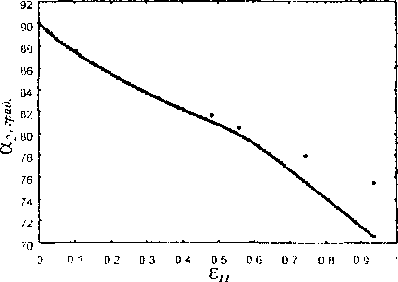
Далее будем считать, что активными могут быть любые системы скольжения. Тогда дифференциалы углов ориентации и деформации материального волокна за счет сдвигов по всем системам найдутся с помощью гипотез о суперпозиции d6 = £>k,    d

k=l где углы 0, <р задают ориентацию материального волокна относительно осей кубической решетки, d6k, d(pk описывают изменение этой ориентации, a dek описывает деформацию материального волокна за счет сдвига по k-й системе. Величины dOk, d

Фиксируя тройку материальных волокон вдоль ребер призматического образца в начальный момент времени, с помощью соотношений (1'),(2'),(3),(4) в любой момент времени могут быть определены деформации этих материальных волокон и искажения углов между ними (рис 2). В силу однородности поля деформаций таким образом будут определены деформации образца. Для удовлетворения гипотезы б) (о направлении образующей) образец должен испытывать поворот как жесткое целое в направлении, обратном мгновенному изменению ориентации волокна т_(| направленного в данный момент вдоль образующей. Соответствующая пара бесконечно малых углов изменения ориентации находится по (Г),(3).

Определенные таким образом деформации не искажают кристаллическую решетку монокристалла, которая, однако, поворачивается вместе с образцом Это следствие предложенной модели согласуется с экспериментами [1,2,4].

В качестве неубывающего параметра процесса выбрано осевое удлинение образца бц с В текущий момент времени при заданном de для волокна иц с использованием (2') и (4) можно получить условие геометрической возможности набора бесконечно малых сдвигов dyk, к=1,...,12

Z (nkbk:mfmf)dYk-de,                                          (5)

k=l где ориентация векторов Ьк и пк выбрана так, что при заданной начальной ориентации оси nif будет nifbk>0 и mf пк>0 (и вследствие неуирочнения систем останется в силе в течение всего процесса). Физически возможный набор сдвигов, удовлетворяющих (5), разыскивается с помощью принципа минимума [4], 12

Z l^dY_k|^P ~>min,                                                      (6)

k=l где р — материальный параметр, связанный с показателем q степенного закона течения (4.2) в [5] как l/p+1/q-l (тогда критерий текучести монокристалла записывается в виде (3.1) в цитируемой работе). Решение задачи (5)-(6) имеет вид de ,            \ч!

dVk=T2--------------(nkbk:nifmf) , к=1,...,12.                           (7)

Z(n_kb_k:m_fm_r)⁴ к=1

Пусть одноосное растяжение образца, ведется с постоянной скоростью осевого удлинения ё, известны начальные конфигурация образца и ориентация решегки монокристалла. Мгновенные деформация и жесткий поворот образца определяются формулами (Г)-(4),(7). Очевидно, изменение ориентации кристаллической решетки определяется тем же поворотом. Таким образом, рассматривая процесс растяжения как последовательность мгновенных деформаций, можно рассчитать актуальные конфигурацию образца и ориентацию решетки монокристалла.

Сравнение с экспериментом. Использовались экспериментальные данные [2] одноосного растяжения двух призматических образцов из монокристалла алюминия, отличающихся начальной ориентацией кристаллической решетки (образцов №59 и №68 [2]). На рис. 2, изображающем форму образца в текущей конфигурации, указаны измерявшиеся в течение экспериментов параметры: ai, аг — углы между образующей inf и материальными волокнами пц, т2, первоначально направленными вдоль ребер прямой призмы, hb Нг — расстояния между ребрами, X — угол между гранями. Согласно предложенной модели eq - arccos(m, mf), а2 - arccos(m2 mf),

(cosa] cosa2 - nij • m^

X — arccosl--5--------------2-------I-                                                        (8)

V sin a2(l + 3cos at) / h^mjsiria],       h2=m2sina2, где m,, 1П2 — длины материальных волокон nil, m2. Помимо деформационных компонент, в ходе опытов измерялась пара углов 0N] ,9N2 между двумя кристаллографическими осями Nj, N2 и образующей. Например, для образца №59 рассмотрены оси <100>, < 1 11>, тогда в терминах модели

- mfl + nip + mn

6100 = arccos( m п), © j н = arccos(-------^-----------~ где inf j , i=l,2,3 — компоненты вектора Шг в осях кристаллической решетки. Авторы работы [2] измеряли также для каждой из использованных кристаллографических осей Nj, N2 угол между проекцией рассматриваемой оси на плоскость, нормальную образующей, и фиксированным в этой плоскости направлением (плоскость и ось фиксированы относительно лабораторной системы координат). Однако гипотезы нашей модели не позволяют зафиксировать либо определить вращательное движение образца в данной плоскости. Для фиксирования начальной ориентации материальных волокон относительно решетки использовались пара углов 9N 9Nz и любой из углов вращения соответствующих осей при е = 0.

Рис. 2. Кинематика деформирования образца:(а) отсчетная, (б) актуальная конфигурации

а

Для нахождения единственной материальной константы модели q по экспериментально полученным зависимостям параметров аь «2, hi, h2, л, 9Л^,9Л. от осевой деформации 6 использовалась следующая процедура. Сначала для каждого параметра определялось значение q, соответствующее наилучшему приближению этого параметра к эксперименту, те. минимизирующее невязку

Mq) = Z(to(e0q)"to(eJ))2, (io)

где to(eJ,q), (о(е!) — соответствующие рассчитанное и экспериментальное значения i-го параметра (i=:l,...,7) в j-й момент растяжения (j=l,.,.,п, п — количество экспериментальных точек). Кривые co(e,q), i = 1,....7 при оптимальных q обозначим to(e), i = 1,...,7. Наилучшее q -= q для всех параметров находится из решения задачи

7                               |itoC,q)-to(-)il

Z Si (q)-»min ,  Sj(q) = ~'                                       0 0

i=i                                 l!®(-)“ ю(е )|| где ||х||= jx(t)|dt. Функция S:(q) имеет смысл отклонения кривой ®(-,q) от ©(•). J                                                                                                                                                              i                          ।

Точность описания эксперимента предложенной моделью при найденном q' определялась значениями относительных невязок

1 2(®(е0 - ю(е'))2

для каждого параметра со и величиной

. 2

V 1=1 для всего опыта.

На рис. 3,4 приведены результаты расчета двух опытов согласно предложенной модели вместе с соответствующими экспериментальными данными. Кривые соответствуют зависимостям co(e,q*) (i=l,...,7). Численный расчет был реализован с шагом 0,0001 по осевой деформации (кратности, а не истинной деформации), что в точности воспроизводит эксперимент. Для эксперимента с образцом №59 (рис. 3) определено q =35,5 и А = 0,41. Несмотря на большое значение ошибки А, поведение кривых описано моделью качественно верно, а основной вклад в А вносит ошибка параметра h2. Ниже приведены погрешности (12) определения всех параметров образца.

Образцу №68 соответствует q‘=30,5 и А=0,13. Рассчитанные кривые, приведенные на рис. 4, также близки к экспериментальным данным, количественные оценки точности описания приведены ниже.

Остановимся подробнее на вопросе описания моделью поворота кристаллографической решетки. Для представления результатов удобно использовать стереографическую проекцию [6]. Каждая точка такой проекции характеризует направление вектора в системе кристаллографических осей решетки, а стереографические координаты точки |х,у) связаны со сферическими координатами соответствующего направления {ф,0} соотношениями sin 9 х = a cos<р, у - a sin ф, а=-------—.

• 1    + cos 9

На стереографической проекции (рис. 5) представлены экспериментальные точки и рассчитанные траектории, задающие изменение направления оси растяжения относительно кристаллографических осей. Рассчитанные траектории (при фиксированном начальном положении оси) качественно различаются в зависимости от значения материального параметра q. Обнаружено существование трех устойчивых кристаллографических направлений <010>,<121> и <111>, к одному из которых стремится ось растяжения в процессе деформации образца в зависимости от начальной ориентации кристаллической решетки и значения параметра q (см. тонкие кривые на рис. 5; для начальных ориентаций оси в рассмотренных экспериментах устойчивое направление <111> недостижимо). Некоторые металлы и сплавы действительно имеют текстуры с одним преобладающим направлением из такого набора или их комбинацией, причем исход зависит главным образом от энергии дефекта упаковки [3].

О 0 1   0 2   0 3   04   0 5   06   0.7   0.0   0 9    1

Рис.З . Результаты расчета согласно предложенной модели в сравнении с экспериментом [2] (образец № 59):

---наилучшее приближение согласно (11) (q* = 35,5);

• • экспериментальные данные

  
  
  
  
  
  
  
  
  
  

  Рис. 4. Результаты расчета согласно предложенной модели в сравнении с экспериментом [2] (образец № 68);

  ---иаилучшее приближение согласно (11) (q* = 30,5);

  • экспериментальные данные

  
  
  
  
  

Расчеты при q = q для соответствующих образцов показали (см рис. 5, выделенные кривые), что ось растяжения сначала движется практически вдоль окружности большого круга, проходящего через начальную точку и полюс <110> Соотношение (7) при больших q делает доминирующей одну систему скольжения (задаваемую векторами п. и Ь.) с наибольшим фактором Шмида (n,b,:m_fm_f), то есть деформации образца фактически реализуются единичным скольжением вдоль этой системы, что соответствует движению оси растяжения вдоль указанной окружности. При осевых деформациях. 0,74 и 0,55 образцов №59 и №68 соответственно ось растяжения достигает симмеграли (прямой на стереографической проекции, проходящей через точки <010> и <111>). Далее движение происходит практически вдоль этой симмеграли до полюса 121 •. Деформация, сопровождающая этот поворот, реализуется скольжением по двум равноправным (имеющим равные факторы Шмида) системам скольжения. Аналогичные “траектории поворота” наблюдались экспериментально в упомянутой работе [2], авторы которой обосновали наблюдаемый вид траекторий в терминах закона Шмида, Предложенная в данной работе модель, учитывающая множественность скольжения и позволяющая определять все параметры деформации образца и поворот его решетки, при достаточно больших значениях константы q, определенной из этих экспериментов, фактически обосновала применимость к описанию явления закона, согласно которому действуют только системы с максимальным фактором Шмида.

Рис. 5. Стереографическая проекция траектории полюса оси растяжения в процессе деформации согласно предложенной модели. Жирная линия соответствует наилучшему приближению ко всем экспериментальным данным, точки ■ экспериментальные данные [2]: (а) образец № 59, (б) образец № 68

Был также проведен расчет для аналогичного эксперимента, описанного в работе [1]. Однако ряд измерений (главным образом ориентации кристаллической решетки), по-видимому, недостаточно точны: точки, отмечающие движение оси растяжения на стереографической проекции, не экстраполируются какой-либо гладкой кривой. Сказанное в какой-то мере относится и к образцу № 59 (см. рис. 5а). Возможной причиной неточности могла быть не полная идеальность монокристаллов, полученных Г. Карпентером и К. Элам для пионерских исследований [ 1,2].

На рис. 3-4 можно заметить, что при деформации е. ~ 0,4-0,5 углы, задающие ориентацию решетки (обозначенные 6), изменяются слабо, достигая 60-65°. Для грубой оценки рассмотрим плоскую модель в рамках прежних гипотез, но с одной системой скольжения с нормалью к плоскости скольжения ориентированной под углом 6 к оси растяжения. В данном приближении легко получить дифференциальное уравнение 9tg0 - X / X = О (X — кратность) и его решение 0 = arccos(exp(-h)cos0o) при О - 6„ при е = 0 (h = InX — истинная деформация). При, а при 6О * л / 2 0 -> л / 2 при h -> да. Оценим, при каком удлинении h. решетка из начального положения 0О = О достигнет 0 = 0,9- к /2: h = -In cosO, 45л » 1,855. В реальности вследствие наличия потенциально могущих работать!2 систем скольжения, 9 не удаляется так сильно от 0о, а обычно на 10-25°. Полученные в работе значения деформаций е* ~ 0,4-0,5 поэтому кажутся правдоподобными. Заметим, что экспериментаторы сообщают, что при логарифмических деформациях фрагментов порядка 0,3 их решетка практически перестает поворачиваться. И здесь наблюдается согласие: h„ = 1п(1 + е,) = 0,34 - 0,41.

В заключение сделаем некоторые выводы относительно причин вращения решетки в опыте на одноосное растяжение. Вращение это вызывается недостатком активных систем скольжения и граничными условиями, заданными на торцах образца (на боковых его поверхностях имеют место тривиальные условия на напряжения). Обычно нагружающее устройство таково, что направление силы на каждом торце неизменно ориентировано относительно его плоскости, и линия действия сил — общая. В процессе растяжения образца относительное смещение блоков кристалла между параллельными плоскостями действующей системы скольжения стремится сместить внешние силы с общей линии их действия. Поскольку нагружающее устройство не разрешает такого движения, на торцах образца должны появиться такие дополнительные внешние силы, которые создают изгибающую образец пару, так что наряду с растяжением он будет испытывать изгиб, а решетка — некоторое поле вращений. За исключением средней части образца поле напряжений в последнем уже не будет представимо диадой а = И (что обычно для опыта на растяжение изотропного образца), а будет описываться несимметричным тензором напряжений Коши. Однако в [1,2] и последующих работах Тейлора информация о перерезывающих усилиях в местах закрепления образца, позволившая бы в более полной мере понять статику процесса, к сожалению, отсутствует, поэтому наш анализ остается ограниченным. Как отмечалось в начале статьи, при испытании достаточно длинного образца упомянутый изгиб обычно локализуется вблизи его концов, а для части, удаленной от концов, эти локализованные места изгиба решетки можно считать “пластическими шарнирами”, так что будет уместной другая идеализация граничных условий: силы закреплены в центрах торцов образца шарнирно, а линия их действия неизменна. В рамках такой модели изгиба решетки происходить не будет, но решетка будет постепенно однородно поворачиваться. По тем же причинам поле вращений решетки неизбежно появляется и при деформировании гюликристаллического тела: объем мезоскопических размеров с однородной ориентацией решетки (зерно или фрагмент поликристалла) также находится под действием сложной системы граничных условий, заданных на внутренних для поликристалла границах этого зерна или фрагмента.

Работа выполнена при поддержке Российского фонда фундаментальных исследований по проекту 98-01-00125