Model of active interaction between internet providers in the context of a multi-agent environment

Let's take a concrete example: this model shows how players A, B, and C transfer information from point S to point T using different edges, such as SX, XY, and so on. Each edge has its own number, which determines the cost of transmitting information for each player using this edge. For example, if the SX edge is used by one, two, or three players, then the cost of transmitting information along this edge will be 2, 3, and 5, respectively. The total cost for each player is calculated as the sum of all costs on each edge along which he transmitted infor-mation[1].

Figure 1. Interaction of information providers

Defining a game using overloaded models.

A model (N,M,⁽Af) Ai i _eN,(C j Cj)j_jeM) is called overloaded if:

N = {1.. n] - set of players

M = {1.. m] is the set of possibilities

For i e N, Ai A_i specifies the set of strategies of player i, where each a , e A aieai is not an empty subset of possibilities

For j e M, je M, j e R ^cjern defines a cost vector, where C j (k~) cjk is the cost for each player using the facility jif k users use this facility.

An overloaded game is related to a model of a game in a strategic form, which involves a set of players N, (a set of strategies f)Ai ieN, and a cost function. We define the cost function as fol- lows: let A = xiEN Ai ai be the set of all possible strategies of the players. For any a E A and for any j E M, let nj(ni"a) be the number of players using the means j, with the assumption of the strategy of using a -.

Then the cost function for supplier i is defined as U i (ta) = Z j=j_iai C j (n j (a))jn ja.

It is important to note that all players are equal in the sense that they have the same "weight". Regardless of which vendor uses the tool, the only thing that matters is how many vendors use it.

Theorem 1 states that every finite game with overloading has a pure strategic equilibrium.

To prove this fact, we consider a certain strategic vector a E A, as shown above.

Let F:A ^ R be a function of potentials defined as F(a) = T J=i Е^ ^ C j (k).

Thus, we can conclude that an overloaded game always has a pure strategic equilibrium.

Let's pay attention to the situation when one of the players changes his strategy from a_a i  to   bi i  (where   a _ab b_bi E A ai ). Let

Au u _i represent the change in payoff due to this strategy change:   Au i = 11 , (1') , , a —, ) —

U i ⁽a i ,a - _l⁾ = y. j _Gbl -aiCj (n j (a) + 1) — T a- _b, c j (n j (a)) (explanation: Au i is equal to the cost of using new resources minus the cost of using resources that are no longer used due to a change in strategy).

Let АФФ F be the potential change caused by changing strategies: AF = F(b_ibi,a — _l') — F⁽a i ,ai, a_D = l /Eb-^ c^n j ld) + 1) — T_ai-bi C j (n j (a)) (explanation: this is the definition of the potential function).

We have proved that when changing the strategy of one player, Ф F = u щ.

This result is interesting: we can start with any specific strategic combination a, and at each step, the player will reduce their costs. This means that F will also decrease at each step. Given that F can only take a finite number of values, we can reach a local minimum. This way, no player will be able to make improvements, and we will get a Nash equilibrium.

The concept of a potential game

Suppose we have a game G=N,Ai,ui in strategic form, where A=*iEN AI is the set of all possible strategic vectors for a given game.6 = (N, (Ai), (ui)) в стратегической форме, где A = XiEN Ai - это множество всех возможных стратегических векторов для данной игры.

The function F:A→R is an exact potential for the game G if for any V a_EA and any ^Va_ib_i ai_biEai   the equal ity   Ф ^(b i , Q ^—

Ф(ai, fbi, a — i — fai, a-t) = uibi, a — i — Ui(bi,a^) — Ui(ai,7a—).

The function F: A ^ R is the weightpotential for the game G if for any VaEAVaa;i,biEbii ai the                      equali- tyФ(bfbi;ci—.), (a-i-fai,a—') = miuiibii (ui(bi,a—,)a—i(ai, —ui ai, 0,4)) = mw iAui, where (mw i)iENis a vector of positive integers (a weight vector).

The function F:A→R is an ordinal potential for a minimal game G if for any V g_EA and any ^V a_i,b_iai,_biEai the condition ^(F(^b bi ^,a4) ^—

F(ai, ai, a,) < 0) ^ (u ibt(bt, a^) — ui(ai,a-l) < 0) (the converse holds for the maximum game).

Note that the first two definitions are special cases of the third definition.

A game G is called an ordinal potential game if it admits an ordinal potential.

Theorem 2. Every final potential game with a certain balance has a pure strategic component.

Proof: As in the previous proof, starting with an arbitrary deterministic strategy vector, after several steps for one player, a local minimum is reached, which, as already explained, represents a certain equilibrium [4].

Accurate Potential Play

Consider an undirected graph G = (V,E) with a weight function m on its edges. Our task is to divide the set of vertices V into two disjoint subsets Dd1 and DD2 (withthe condition D1 U DD2 = V). For each player i, the value sSi E {—1,1}is chosen, where sSi = 1 means that i belongs tothe subset D1, and vice versa for DD2. The weight on each edge determines how strongly the corresponding vertices "want" to be in one subset. For player i, the cost function Ui5i(5) = Z;^i is defined as the sum of all MijSiSj ©ijsisj, where j^i#i[3].

In the example shown in Figure 2, you can see that players 1, 2, and 4 are not interested in changing their strategies. However, player 3 is not satisfied with the current state, and he can increase his profit by changing his chosen set to D1.

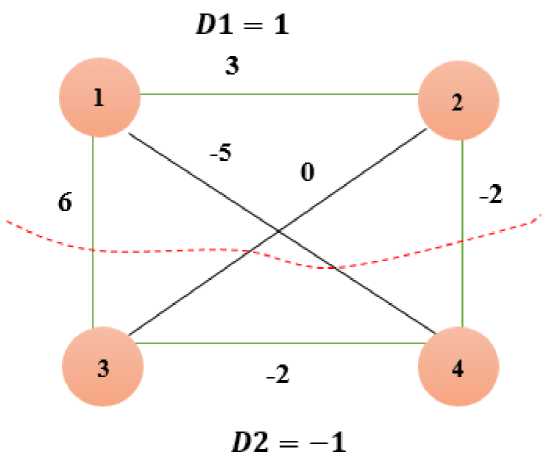
Figure 2. Visual example of anaccurate potential game

Applying the potential function F (S') = Xjj, we consider the case when one player i changes his strategy, moving from one set to another:   ku =

T. j j^i,j^Si^{jS i S}j -Lj^i ^ij^(-Si^)sj = 2Lj*iWij^Si^Sj = ^2Lj.jMij^Si^Sj + 2^Lj:i^wiJ^Si^Sj = ^k(F'⁾-

This means that the function F is an exact function of the potential, and therefore we can conclude that this game is an exact potential game.

The example shows an overloaded game in a network segment where there are two information providers, one server and one client. In this case, we consider a section of the network G = (V,E) with a delay function cCj £ RnRn. One of the information providers, let's call it Provider i, aims to establish a minimum-latency route between server S and client T[1].

The example considered here is a situation where N={1,2}. In the original position shown in Figure 2 (left), the red information provider (supplier 1) has a delay of 45, while the blue information provider (supplier 2) has a delay of 70. Information provider 1 can reduce the delay for transmitting information from gateway S to T, so it chooses a different route, as shown in Figure 2 (on the right). And as a result, the delay of information provider 1 is reduced to 29.

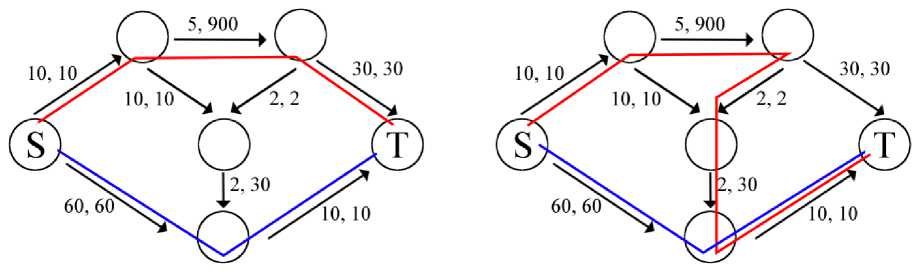
Figure 3. Method for reducing the delay in transmitting information

Another method for reducing the delay in transmitting information is offered by information provider 2[2]. It transmits packets from host S to host T along the route shown in Figure 3, which reduces the delay to 60, while simultaneously increasing the delay of information provider 1 to 57.

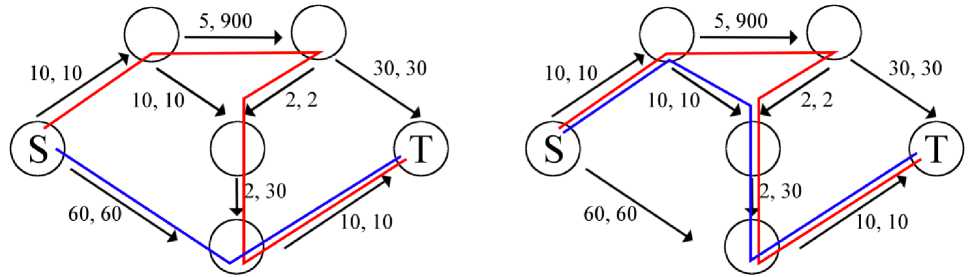
Figure 4. Optimizing data transfer latency

To increase transmission efficiency, information provider 1 can use an alternative route shown on the right side of Figure 4.This approach will reduce the delay time to 45, and information provider 2 – to 32.

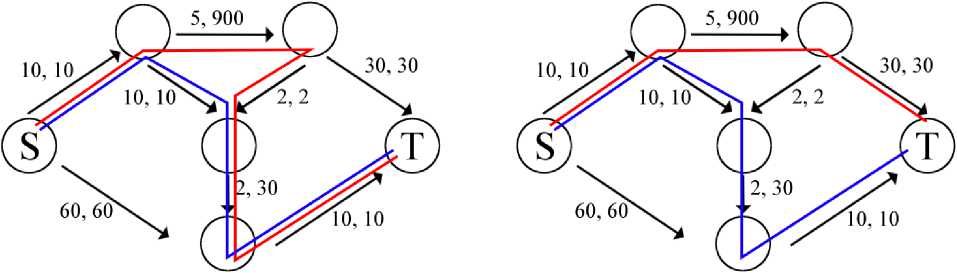
Figure 5. Achieving Nash equilibrium.

The consequence of the above is to achieve a Nash equilibrium, since no information provider is able to reduce the delay in data transmission[5].

As a result of the work done, the following conclusion can be drawn: the task has been fully investigated and illustrated using various examples. In the course of our research, we confirmed that the Nash equilibrium is achieved in the considered examples.

Thus, the goal of the work was successfully achieved. The model of active interaction between Internet service providers in the context of a multi-agent environment is an effective tool for optimizing the work of providers, increasing the level of user service and reducing the cost of services provided. It is important to develop and apply models of active interaction, taking into account the specifics of Internet service providers and the features of a multi-agent environment.