Модель определения коэффициента диффузии в растворах электролитов

Жигжитова С. Б., Балданова Д. М., Бадмаев С. С. Модель определения коэффициента диффузии в растворах электролитов // Вестник Бурятского государственного университета. Химия. Физика. 2024. Вып. 2. С. 3–7.

Диффузия ионов зависит от подвижности ионов, их способности двигаться в среде, а также от коэффициента вязкости среды, который влияет на скорость диффузии. Все эти параметры важны при изучении процессов диффузии ионов.

Согласно Дебаю-Фалькенгагену ионы могут совершать гармонические колебания в неравновесных условиях. Движение ионов в процессах диффузии обусловлено градиентом концентрации вещества. Потенциальная энергия взаимодействия ионов определяется следующим выражением:

U = 2 E ea^a • где ea — заряд иона; ^a — потенциал. Известно, что ea^a = Ua . Тогда U = | EUa •

при сложении энергии U _a появляется множитель 1/2, поскольку она учтена дважды. В соответствии с законами механики движение ионов при диффузии возможно только под действием силы F_a :

dU a

F n =--

a .

dr

Таким образом, учитывая данные условия, ¹ a ₂

F _a можно представить в виде: dU a

dr

.

Эффективная сила F _эф связана с F _a следующим соотношением (4):

F =

Fэф

_y dUa = 2f

dr a

.

Запишем силу Стокса для ионов, принимая их за сферические объекты:

( R^Fa = 6n^R 1 + - V •

V   rD )

здесь П — вязкость; R — радиус сольватированных ионов; r _D — дебаевский радиус и V — скорость ионов [2].

Следовательно, эффективную силу можно представить:

F* = 2 ■ 6 nn R 1 + - |v .

V ^rD )

Подвижность b — это отношение скорости движения ионов V к эффективной силе эф

b = V-

F эф

R^ ’ 2 • 6 nn R 1 + —

V   rD )

С другой стороны, по закону Эйнштейна подвижность можно представить через диффузию

b=-D- kT

Б

.

Коэффициент диффузии можно получить, объединив уравнения (7) и (8:

D = ¹ •

kT

Б

( r\

6 nn R 1 + -

V r D J

здесь ⁿ — коэффициент вязкости, равный [1]

П =

N A e ² exp( - —) 411 •Ю ^{- 12}

Б

6 n AR (1 + —) r_D

Тогда, подставив вязкость (10) в формулу (9), получим окончательное выражение, позволяющее рассчитать коэффициент диффузии:

kJA

Б

^ Ш

Ne ² exp•I.II • 10 ^{1 a}

V ^кБ^Т J

Результаты расчета коэффициента диффузии для водных растворов по формуле (11) приведены ниже.

Для хлорида цезия CsCl при 25 °С

Таблица 1

C, моль/л	0,1	0,5	1	2	3	5
Ʌ, Ом-1 см2моль-1	128	118	113	107	98,7	85
D теор·10-5 , см2·сек- 1	1,62	1,75	1,87	1,90	1,95	2,01
D лит [3]	-	1,86	1,91	2,09	-	-

Для хлорида натрия NaCl при 25 °С

Таблица 2

С, моль/л	0.001	0.005	0.01	0.1	0.5
Л , Ом-1 см2моль-1	123	111	118	106	93
D pac4 •Ю" 5, см2сек-1	1,653	1,556	1,160	1,517	1,450
Dлиm •Ю " 5 , см2сек-1	1,584	1,506	1,544	1,482	1,469

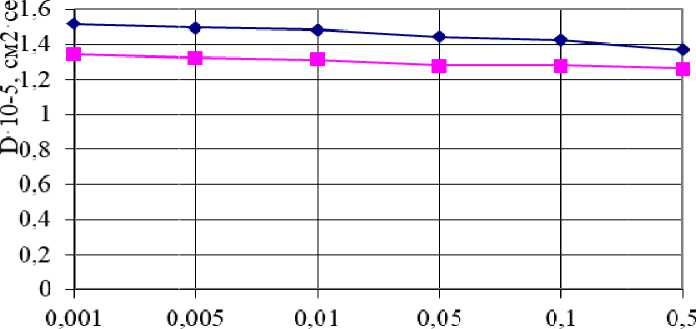
>- расч -в- лит             С, моль/л

Рис. 1. За в ис им о ст ь ко э ф фициент а д иффуз ии D хлорида лития LiCl от концентрации при 25 °С

Заключение

Т а к и м об р а зом , ре з ультаты исследования показывают, что ис по льзование у равн ен и я ( 11) для оц енки диффузии в системе было эффективным. Лит е р а т урные значения и зн аче н и я, полученные путем расчета, совпадают в пр ед ел а х по г решн о ст и . Это г овори т о т ом, чт о для анализа процессов диффузии в рассматриваемой системе п ред ложенный метод оценки диффузии может быт ь п рим ен ен с д ос т аточн ой т очн ос т ь ю .