Модель определения рационального объема запасов продукции в цепях поставок со случайным спросом
Автор: Анисимов В.Г., Анисимов Е.Г., Сауренко Т.Н., Смоленский А.М.
Журнал: Вестник Академии права и управления @vestnik-apu
Рубрика: Вопросы экономики и управления
Статья в выпуске: 1 (46), 2017 года.
Бесплатный доступ
В статье предложена модель для определения рационального объема запасов продукции при фиксированном периоде их пополнения и случайном спросе. В модели учтена характерная для реального спроса конечность количества потребителей продукции. Это позволило более адекватно, чем при использовании традиционных моделей, определять рациональные объемы запасов продукции в цепях поставок. Вместе с тем учет конечности и априорной неизвестности количества потребителей и объемов востребованной каждым из них продукции, привел к необходимости разработки нового подхода к моделированию спроса. Этот подход определил основное отличие предложенной в статье модели от традиционных.
Цепи поставок, рациональные объемы запасов, случайный спрос, модель
Короткий адрес: https://sciup.org/14120160
IDR: 14120160 | УДК: 338.984
Текст научной статьи Модель определения рационального объема запасов продукции в цепях поставок со случайным спросом
В ведение. Создание запасов в цепях поставок объективно обусловлено необходимостью непрерывного обеспечения спроса на продукцию и невозможностью или экономической нецелесообразностью полностью совмещать объем и сроки поставок продукции с моментами возникновения спроса на нее. Вместе с тем создание запасов связано с дополнительными затратами на строительство соответствующих складов, создание запасов их хранение и обслуживание. Следовательно, возникает задача определения рациональных объемов запасов продукции. Разработка модели, обеспечивающей ее решение в условиях фиксированного периода пополнения запасов продукции и случайного спроса на нее, составляет цель настоящей статьи.
Описание модели. Вопросы определения рациональных объемов запасов продукции в различных условиях рассматривались в работах [11,12,9,15,8,14,13]. В основу предлагаемых в этих работах моделей и методов решения рассматриваемой задачи положены те или иные варианты формализации процесса спроса в виде предельных распределений для сумм независимых случайных величин. Вместе с тем реальный спрос связан с суммированием конечного (то есть не предельного), но априори неизвестного числа случайных величин [7,2,1,3]. Это обстоятельство учтено в предлагаемой в статье модели для определения рационального объема запасов продукции в цепях поставок со случайным спросом.
Введем обозначения:
Т – длительность периода пополнения запасов продукции;
J – количество видов продукции (номенклатура запасов);
Nj – случайная величина, характеризующая количество потребителей, обратившихся за продукцией j -го в течение времени Тj ;
βrj – случайная величина, характеризующая объем продукции j -го вида, запрашиваемый r -м ( r =1,2,…, Nj ) потребителем;
Хj – объем запасов продукции j -го вида.
При принятых обозначениях объем продукции j -го вида, запрашиваемой за период времени Т , характеризуется случайной величиной:
¥,=^^. j = W;J. (1)
/-0
С учетом (1) рациональность объема запасов продукции j -го вида характеризуется вероятностью Fj ( Xj ) события, состоящего в том, что ( Yj ≤ Xj ). Следовательно, для определения рационального объема запасов продукции j -го вида при фиксированном периоде их пополнения и случайном спросе необходимо построить функцию распределения случайной величины Yj объема спроса на эту продукцию.
Для ее построения вероятность события, состоящего в том, что случайная величина
Nj
примет значение
n
, обозначим
pnj
. Кроме того, будем полагать, что случайные величины
βrj
(
r
=1,2,…,
Nj, j
=1,2,…
J
) запрашиваемых потребителями объемов продукции
j
-го вида – независимы, имеют одинаковые для каждого вида продукции распределения и независимы от
n
. Тогда для определения функций распределения
Fj(y) = Fj(Yj
Характеристическою функцию случайных величин βrj ( r =1,2,…, Nj , j =1,2,…, J ) обозначим φ0j (ξ) . Тогда, на основе мультипликативного свойства характеристических функций, характеристическая функция случайной величины Yj ( j =1,2,…, J ) может быть записана в виде [5,6]:
ФА^^Рп^А^ j-U,..,J. (2)
и=0
С учетом (2), плотность распределения
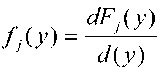
случайной величины Yj ( j =1,2,…, J ) имеет вид:
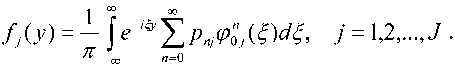
Из (3), вследствие конечности выражения t-P-A® 5 ILpXW < », j = 1,2,..J /7=0 и=0
следует:
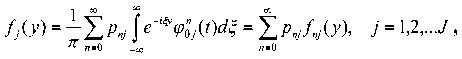
где fnj(y) – плотность распределения суммы n случайных величин βrj ( r =1,2,…)
Из (4) следует, что вероятность отсутствия дефицита продукции j -го ( j =1,2,…, J ) вида при объеме Хj ее запасов определяется соотношением
FAy ^ ^) = t^Pnj U'AyW, j = i,2,.v• (5)
w=0 о
С учетом (5), вероятность отсутствия дефицита по всей номенклатуре продукции определяется соотношением
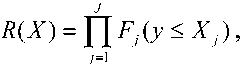
а вероятность дефицита хотя бы по одной номенклатуре продукции – соотношением
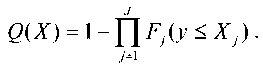
Соотношения (5) – (7) составляют основу ряда моделей оптимизации объемов запасов продукции при фиксированном периоде их пополнения и случайном спросе. Для их построения введем обозначения:
cj – стоимость содержания единицы запасов продукции j -го вида;
gj – вес единицы продукции j -го вида;
vj – объем единицы продукции j -го вида.
Тогда общая стоимость содержания запасов продукции определяется соотношением
С(Х) - ^С]Х, • (8)
7=г
Общий вес запасов продукции определяется соотношением
G^^g/j, (9)
7=1'
а их общий объем – соотношением
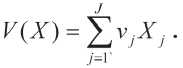
С учетом соотношений (6) – (10) можно построить следующие задачи оптимизации объемов запасов продукции при фиксированном периоде их пополнения и случайном спросе [4,10].
Задача 1. Определить объем запасов X* = {X * 1, X2 * ,… XJ * } , обеспечивающий минимизацию стоимости их содержания
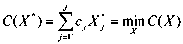
при заданной вероятности R*(X) отсутствия дефицита
R^ = f] F^
7=1
и ограничениях на допустимый вес G* и объем V* запасов:
G(X^ygjXj K(X) = Y v,.X, v 7 ti J .1 7=1' Задача 2. Определить объем запасов X* = {X1*, X2*,… XJ*}, обеспечивающий максимизацию вероятности отсутствия дефицита по всей номенклатуре продукции или минимизацию вероятности дефицита хотя бы по одной номенклатуре продукции gCX^minii-H^Cy^jr,)](15a) 7=1 при ограничениях на стоимость C* содержания запасов, их вес и объем: C(X^yCjX. G(X) = ^gjX f < G”, 7=1' JZ(^) = yVjXj < v\(18) 7=r Конструктивные методики решения этих задач получаются путем установления законов распределения случайных величин, характеризующих поток потребителей и запрашиваемых ими объемов продукции. Для определенности будем полагать, что: количество потребителей продукции j-го вида за период T подчиняется закону Пуассона с параметром μj, то есть объем продукции, запрашиваемый каждым потребителем, имеет показательное распределение с параметром λj: w^yVX^, j = l,2,...,J. (20) Характеристическая функция экспоненциально распределенной случайной величины имеет вид <р0Д) = (А-1^'у'. (21) Подставив (19) и (21) в (2), получим: Подставив (22) в (4), после преобразований получим: 7',(.rl = ^X je-»u,-^r^=I, ----------, j = 1.2....,j. (?3) (23 где Г(n) – гамма-функция. Из (23) следует, что что при принятых допущениях вероятность отсутствия дефицита продукции j-го (j=1,2,…,J) вида при объеме Хj ее запасов определяется соотношением Подстановка соотношения (24) в (12) и (15) обеспечивает конструктивность задачам оптимизации объемов запасов продукции при фиксированном периоде их пополнения и случайном спросе. Заключение. В целом полученные соотношения (1) – (18) представляют обобщенную модель определения рационального объема запасов продукции в цепях поставок со случайным спросом. Соотношения (19) –(24) конкретизируют эту модель для случая пуассоновского потока потребителей и экспоненциального закона объема потребностей каждого из них.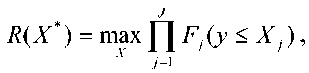
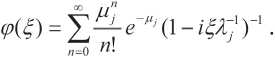
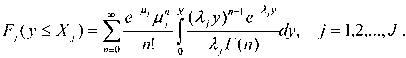
Список литературы Модель определения рационального объема запасов продукции в цепях поставок со случайным спросом
- Авдеев М.М. Информационно-статистические методы в управлении микроэкономическими системами. Международная академия информатизации. С-Пб, Тула: Изд-во Гриф и К. (Тула), 2001. 139 с.
- Анисимов В.Г., Анисимов Е.Г., Капитоненко В.В. Экономико-математические методы и модели в мирохозяйственных связях: учебник. Москва: изд. Российской таможенной академии. 2011.179 с.
- Анисимов В.Г., Анисимов Е.Г., Родионова Е.С., Сауренко Т.Н. Математические методы и модели в экономическом и таможенном риск-менеджменте. Монография/Санкт-Петербург. Информационный издательский учебно-научный центр «Стратегия будущего», 2016. 236 с.
- Анисимов Е.Г. Методические положения математического моделирования задач адаптивного распределения дискретных ресурсов при управлении войсками и оружием в режиме реального времени//Известия Российской академии ракетных и артиллерийских наук. 2016. № 1 (91). С. 32-37.
- Бажин Д.А. Модель оценки эффективности информационного обеспечения применения высокоточного оружия в контртеррористических операциях//Вопросы оборонной техники. Серия 16: Технические средства противодействия терроризму. 2015. № 1-2. С. 44-53.


