Модель оптимизации прибыли авиакомпании

Решение задач оптимизации управления перевозками далеко не всегда может быть сведено к типовой транспортной задаче [1]. Современные авиакомпании представляют собой гигантские предприятия, включающие разнопрофильные бизнесы [2]. Основная деятельность компаний по перевозке пассажиров и/или грузов также имеет сложную структуру и характеризуется большим количеством параметров. Очевидно, что принятие управленческих решений для подобных предприятий требует применения экономико-математических методов и ИТ. При этом имеет смысл выделять в отдельные подзадачи оптимизацию тех или иных видов перевозок и моделировать бизнес-процессы с введением необходимых и возможных упрощений.

Постановка задачи

В данной статье предложено решение проблемы оптимизации пассажирских авиарейсов по различным направлениям, расписания рейсов, цены билетов, выбора оптимального воздушного судна и других факторов, что будет способствовать максимальному увеличению прибыли авиакомпании в зависимости от спроса и конкуренции, а также минимизации операционных издержек [3].

К параметрам оптимизации [4] при данной постановке задачи относятся: пассажиропоток, маршруты, расход топлива, состав авиапарка и другие издержки. Цель – найти оптимальное сочетание цен на билеты, количества пассажиров и типов самолетов, следовательно, максимизировать прибыль или минимизировать разницу между доходами от продажи билетов и издержками на выполнение рейсов.

Модель

В соответствии с поставленной целью необходимо построить математическую мо дель [5] и определить целевую функцию, которая учиты вала бы цену билетов, количе-

Забулонов Алексей Сергеевич магистр, Институт информационных систем и инженерно-компьютерных технологий, Российский новый университет, Москва. Сфера научных интересов: системный анализ, управление и обработка информации, искусственный интеллект.

ство пассажиров, издержки на топливо и обслуживание, а также постоянные расходы на рейс [2].

В общем случае

Прибыль = Цена билетов х Пассажиропоток - Издержки.

В качестве параметров целевой функции можно использовать цену билета, расход топлива, расстояние и уровень обслуживания.

Раскроем эти понятия:

• •    пассажиропоток – количество пассажиров на каждом маршруте;

• •    маршруты – направления, по которым выполняет рейсы авиакомпания;

• •    расстояние – протяженность маршрута;

• •    топливо – расход топлива на каждом маршруте;

• •    авиапарк – количество и тип самолетов авиакомпании;

• •    обслуживание – уровень обслуживания на каждом маршруте (например, питание, развлечения);

• •    издержки – переменные и постоянные расходы авиакомпании, связанные с выполнением рейсов;

• •    цена билета – стоимость билета на каждый маршрут.

Введенные нами ограничения:

• -    вместимость самолета – количество пассажиров, которое может вместить каждый тип самолета;

• -    частота полетов – максимальное количество рейсов, которое может быть выполнено на каждом маршруте за определенный период времени.

Вместимость самолетов является ключевым ограничением, определяющим максимальное количество пассажиров, которые могут быть перевезены на каждом маршруте. Это означает, что нельзя превысить определенное число пассажиров для каждого типа самолета, учитывая их размер и возможности посадки.

Модель оптимизации прибыли авиакомпании

Частота полетов также ограничивает возможность выполнения рейсов. Каждый маршрут имеет максимальное количество рейсов, которое может быть выполнено за определенный период времени, например, за день или неделю. Это означает, что нельзя превысить определенное количество полетов на каждом маршруте в течение этого периода.

Соответственно, целевая функция будет иметь вид

Maximize: ∑(T_ij × P_ij) – (∑(V_f × C_f × F_ij × P_ij) + ∑(V_c × D_i × P_ij) + ∑V_o) где

• •    T_ij – цена билета на маршруте i на самолете j;

• •    P_ij – количество пассажиров, летающих по маршруту i на самолете j;

• •    V_f – переменные расходы на единицу топлива (включает цену топлива и другие расходы, связанные с его использованием);

• •    C_f – расход топлива на одного пассажира за единицу расстояния;

• •    F_ij – расстояние маршрута i;

• •    V_c – переменные расходы на одного пассажира за единицу расстояния (не связанные с топливом);

• •    D_i – расстояние маршрута i;

• •    V_o – постоянные расходы на рейс.

Соответственно, две части функции – это доходы:

• •    T_ij × P_ij – суммарный доход, полученный от продажи билетов на все маршруты i с использованием всех типов самолетов j;

• •    T_ij – цена билета на маршруте i на самолете j;

• •    P_ij – количество пассажиров, летающих по маршруту i на самолете j;

расходы:

• •    ∑(V_f × C_f × F_ij × P_ij) + ∑(V_c × D_i × P_ij) + ∑V_o – суммарные расходы, связанные с выполнением рейсов;

• •    V_f – переменные расходы на единицу топлива (включает цену топлива и другие расходы, связанные с его использованием);

• •    C_f – расход топлива на одного пассажира за единицу расстояния;

• •    F_ij – расстояние маршрута i.

• •    V_c – переменные расходы на одного пассажира за единицу расстояния (не связанные с топливом);

• •    D_i – расстояние маршрута i;

• •    V_o – постоянные расходы на рейс.

Решение задачи оптимизации заключается в нахождении значений P_ij и T_ij, которые отвечают максимуму целевой функции.

Уточним, что в предложенной модели критически важными параметрами являются:

• -    вместимость самолетов – необходимо учесть максимальную вместимость каждого типа самолета при планировании расписания полетов и распределении пассажиров по маршрутам;

• -    частота полетов – необходимо обеспечить максимальное количество рейсов, которое может быть выполнено на каждом маршруте за определенный период времени, чтобы не нарушать ограничения по частоте полетов;

• -    цена билетов – цены на билеты должны быть определены таким образом, чтобы максимизировать прибыль, учитывая пассажиропоток и издержки, связанные с выполнением рейсов;

• -    издержки – необходимо учитывать как переменные, так и постоянные издержки, связанные с выполнением каждого рейса, включая затраты на топливо, обслуживание, аэропортовые сборы и другие операционные расходы [6; 7].

При этом необходимо абстрагироваться от некоторых деталей и переменных, которые могут влиять на прибыль авиакомпании, но не критичны с точки зрения основных ограничений и целей задачи [8; 9]. Например:

• -    динамика спроса – предполагается, что спрос на билеты остается постоянным в рамках определенного временного периода, в реальности спрос может изменяться в зависимости от времени года, событий и других факторов;

• -    конкуренция – не учитывается влияние конкуренции на рынке авиаперевозок и возможные реакции конкурентов на цены авиакомпании и расписания полетов;

• -    сложность операций – в реальной жизни может возникнуть ряд операционных сложностей [10], таких как задержка рейсов, отмена, технические проблемы и др., которые также могут влиять на прибыль компании, но не рассматриваются в данной модели.

Эти предположения помогают упростить модель и сделать ее применимой для решения задачи оптимизации прибыли авиакомпании методом математического программирования.

Решение задачи

Для решения задачи оптимизации выбран метод линейного программирования [4]. Можно предложить использовать, например, симплексный метод или метод внутренних точек.

Результаты оптимизации будут представлять собой оптимальные значения P_ij и T_ij. Авиакомпания может использовать эти значения для определения оптимального количества пассажиров, которых следует перевозить на каждом маршруте с использованием каждого типа самолета, а также оптимальной цены билетов на эти маршруты.

Для автоматизированного решения данной оптимизационной задачи разработана программа на языке Python с использованием библиотек PuLP и Matplotlib. Код программы приведен на Рисунке 1.

Модель оптимизации прибыли авиакомпании

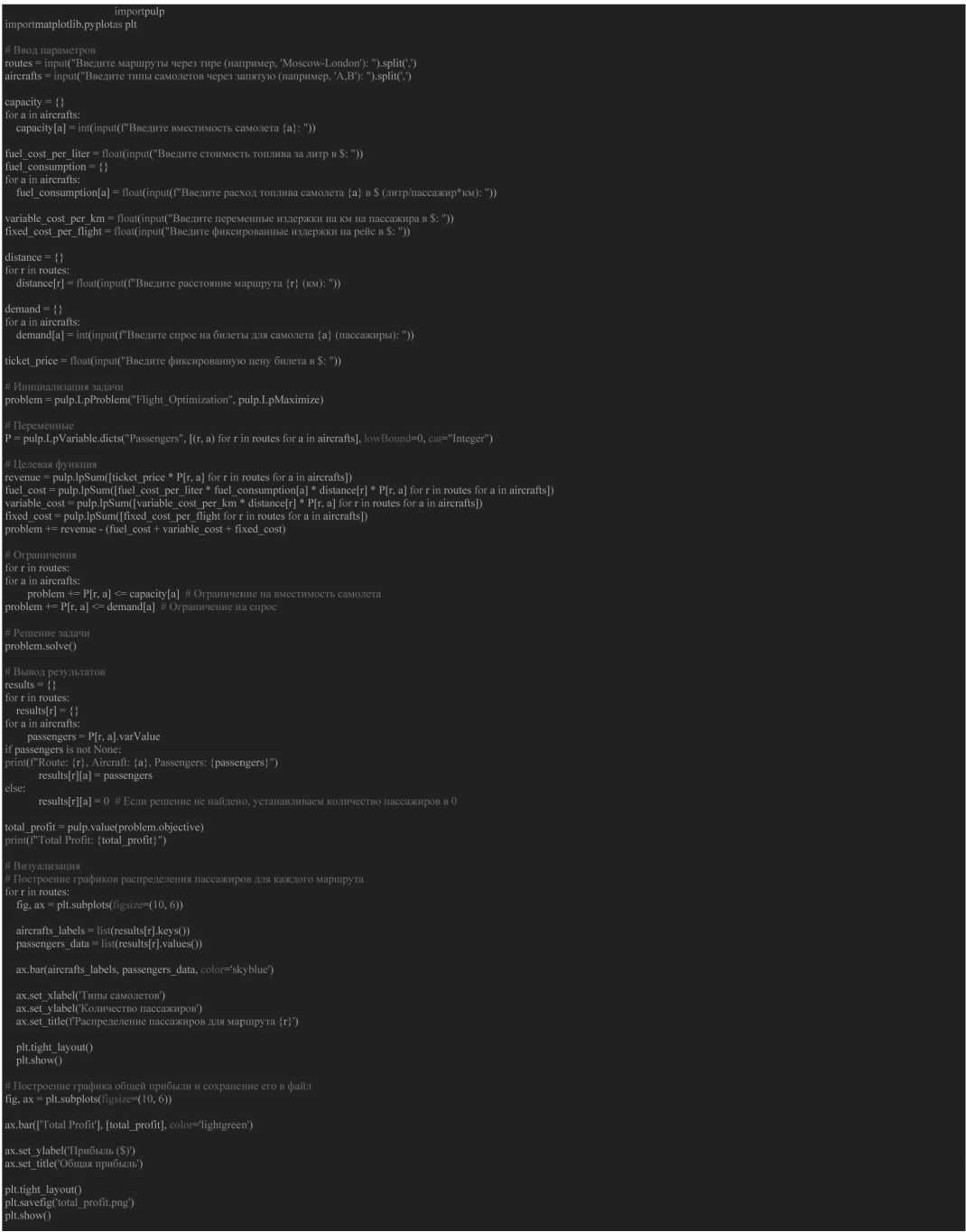
Рисунок 1. Код программы

Источник: рисунки 1 и 2 выполнены авторами.

Код представляет собой программу для оптимизации прибыли авиакомпании на основе заданных параметров, таких как вместимость самолетов, расход топлива, стоимость билетов и др.

Рассмотрим алгоритм работы программы.

• 1.    Ввод параметров. Пользователь вводит информацию о маршрутах, типах самолетов, их вместимости, стоимости топлива, расходе топлива, переменных издержках в километрах на пассажира, фиксированных издержках на рейс, расстоянии между маршрутами, спросе на билеты для каждого типа самолетов.

• 2.    Инициализация задачи . Создается модель оптимизации при помощи библиотеки PuLP, которая предоставляет удобный интерфейс для решения линейных задач оптимизации.

• 3.    Переменные. Создаются переменные, которые представляют количество пассажиров, перевозимых на каждом маршруте для каждого типа самолетов.

• 4.    Целевая функция . Задается целевая функция, которая максимизирует прибыль авиакомпании, учитывая доход от продажи билетов и вычет издержек на топливо, переменные издержки и фиксированные издержки.

• 5.    Ограничения . Устанавливаются ограничения на количество пассажиров, которое может вместить каждый тип самолетов, а также на спрос на билеты.

• 6.    Решение задачи. Выполняется решение оптимизационной задачи, чтобы найти оптимальное количество пассажиров на каждом маршруте для каждого типа самолетов.

• 7.    Вывод результатов . Выводится информация о количестве пассажиров на каждом маршруте для каждого типа самолетов, а также общая прибыль авиакомпании.

• 8.    Визуализация . С помощью графиков демонстрируется распределение пассажиров по маршрутам для каждого типа самолетов. Также строится график общей прибыли.

• 9.    Сохранение графика . График общей прибыли сохраняется в файл total_profit.png.

Решение позволяет авиакомпании оценить и оптимизировать прибыльность своих рейсов, учитывая различные факторы, такие как вместимость самолетов, спрос на билеты и стоимость топлива.

На Рисунке 2 представлен пример вывода программы.

Модель оптимизации прибыли авиакомпании

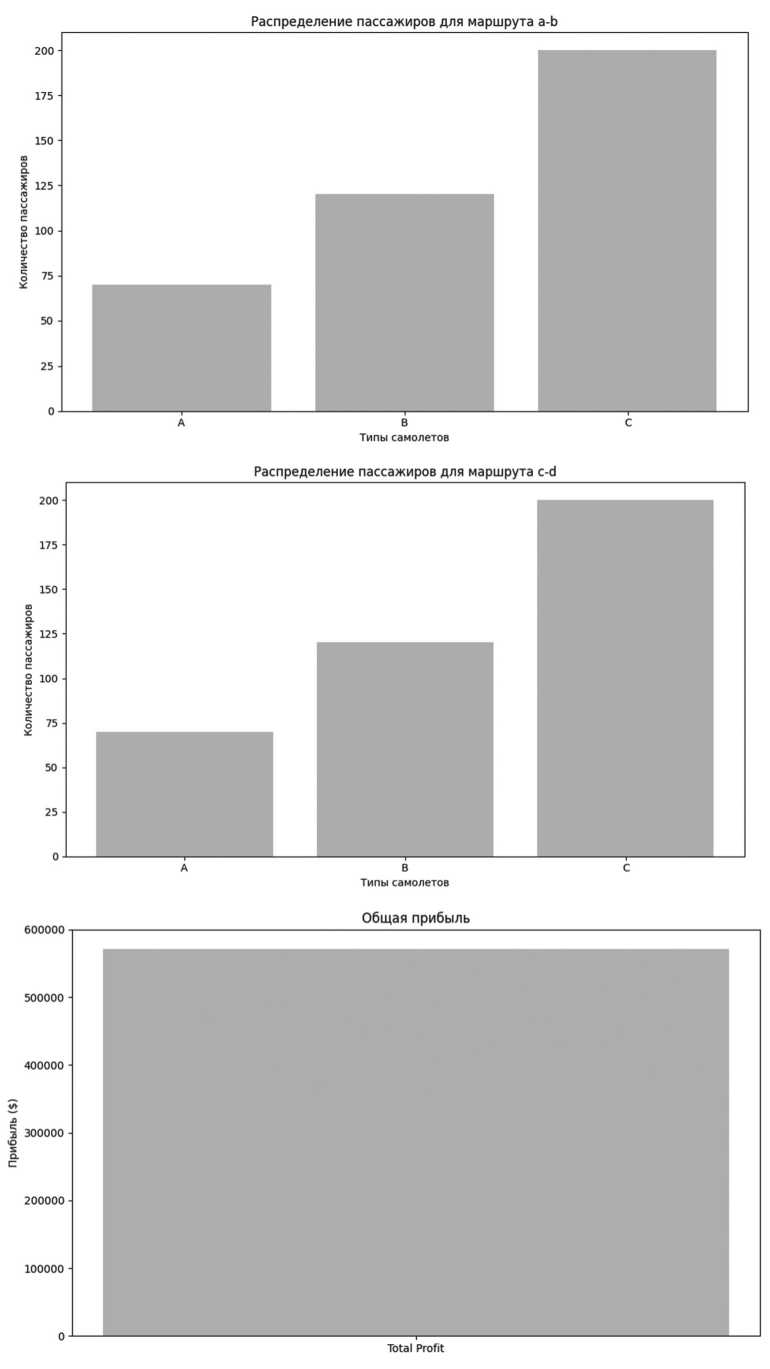
Рисунок 2. Пример вывода программы

Заключение

Показано решение задачи для случая трех типов самолетов по двум направлениям. При этом важнейшим достоинством данного решения является возможность его масштабирования. В целом предложенный подход имеет значительный прогнозный потенциал, поскольку в модели учтены все критические параметры оптимизации [6; 8], что обеспечивает корректность решения; при этом введены упрощения, позволяющие решать задачу максимально эффективно.