Модель организации процесса тестирования

Формально общую модель технологии тестирования можно представить как

Z 1 = F ( Z , U , R , Е ),

U = U ( VAL , REL , REP , KSM ( POL , CHL )),

R = R ( S , V ).

Рассмотрим факторную модель тестирующей системы:

Z1 = F(VAL, REL, REP, POL, CHL, Z, V(S, CR)), где

Z 1 – результат, т.е. показатель качества усвоенного материала студентом, полученного по завершению тестирования.

F (*) – описывает наличие функциональной (стохастической) зависимости между факторами.

VAL – показатель валидности теста по содержанию (может принять любое значение от 0 до 1). Показатель 1 означает, что, по мнению эксперта, вопросы теста корректно и целесообразно сформулированы для оценки качества усвоенных знаний.

REL – показатель релевантности (изменяется от 0 до 1), т.е. вопросы принадлежат тестируемой предметной области. Показатель равен 1, если, по мнению эксперта, вопросы полностью из тестируемой предметной области.

REP – показатель репрезентативности или представительности (изменяется от 0 до 1), т.е. все стороны (части) изучаемой предметной области, по мнению эксперта, отражены и представлены в тесте.

POL – тип вопросов, направленных на установление полноты усвоенных материалов. Это означает, что вопросы специально сформированы для оценки наличия у студента знаний типа фактов. Знания конкретных данных, определений, понятий, объектов из изучаемой (осваиваемой) предметной области.

Ниджрес Моатаз Талал. Модель организации процесса тестирования 155

CHL – тип вопросов, направленных на установление наличия знаний о целостности предметной области. Этот тип вопросов направлен для оценки знаний причинно-следственных связей между объектами, явлениями, понятиями, процессами, методами, технологиями и в целом организационной структуры (целостности) осваиваемой предметной области. Ответы на этот тип вопросов характеризуют не только наличие разрозненных знаний, но и понимание целостной (системной) организации предметной области.

Будем считать, что в нормированном на полноту и целостность тесте должно быть 50% вопросов на полноту и 50% – на целостность. Этот факт эксперт фиксирует как POL = CHL = 0,5. Если имеется «перекос» по типу вопросов, то этот факт отмечается, например, как POL = 0,8; CHL = 0,2 (80% вопросов на POL и 20% – на CHL).

Z – латентный (скрытый в когнитивной сфере) показатель качества усвоенного материала студентом, которую мы собираемся оценить как можно точнее.

V – величина продолжительности тестирования. В свою очередь, выбор значения этой величины зависит от величины S – сложности теста, а также от величины CR – быстроты реакции студента, т.е. от метрик психологических и интеллектуальных особенностей студента.

Считается, что измерительный инструмент тестирования может обеспечить точность D Z , если abs(Z – Z1) ≤ D Z , т.е. абсолютная величина разности величин Z и Z 1 не превышает какую-то величину D Z [4].

Допустим, имеется тестовая система (инструментальное средство), где эксперт установил, что тестирующая система как инструмент имеет значения параметров VAL = REL = REP = KSM = 1, т.е. в нашем распоряжении имеется идеальный по содержанию тестирующий инструмент с показателем качества U = 1. Этот инструмент на конструктивном уровне также полностью защищен от фальсификации результатов, т.е. значение параметра Е = 1. На базе этого инструмента необходимо организовать процесс (процедуру) тестирования с показателем качества R = R ( S , V ) → 1. Эта цель может быть достигнута, если эксперт оценил точно сложность теста (значение параметра S ), а также точно оценил необходимую продолжительность тестирования в зависимости от его сложности (значение параметра V ). Разумеется, что студенту для ответа на вопросы теста необходимо значительно больше времени, чем эксперту, т.е. V >>  S . При этом выбор времени V должен быть обоснован, так как излишнее увеличение времени V не приведет к улучшению значения качества ответов студента, а время будет потрачено впустую.

Очевидно, что каждый студент в зависимости от его индивидуальных особенностей ответит на вопросы теста за разное время. Продолжительность ответа студента рассмотрим как случайную величину X . Следует особо подчеркнуть, что в данной работе авторы не интересуются причинами (их может быть много: психологические, интеллектуальные и др.), почему разные студенты имеют разные значения величины X , т.е. имеют разную продолжительность реакции ответов на вопросы теста даже при наличии у них знаний одинокого качества. Сразу отметим, что авторы владеют большими массивами статистических данных – значений случайной величины X .

Оценка сложности теста

Методика оценки сложности теста, т.е. величины S , следующая. Эксперт получает случайный вариант теста и оценивает сложность каждого вопроса по его трудоемкости (оценивается в минутах работы (мин/раб.) эксперта) (табл. 1).

156 в ыпуск 3/2020

Таблица 1

Пример бланка оценки трудоемкости теста экспертом

№	Вопросы	Ответы	Сложность (мин/раб.)
1	Вопрос	Ответ	1
2	Вопрос	Ответ	3
3	Вопрос	Ответ	2
4	Вопрос	Ответ	1
...	...	...	...
10	Вопрос	Ответ	2
Сложность (трудоемкость) теста S = 20

Таким образом, эксперт оценил сложность ( трудоемкость ) теста равным S = 20 (мин/раб.).

Теперь необходимо оценить значение величины V ( предельную продолжительность тестирования студента ), которая зависит от значения детерминированной величины S ( сложность теста ) и случайной величины X ( продолжительность реакции студента ). При этом случайная величина X может вести себя по-разному (иметь разный закон распределения) в зависимости от подготовленности или неподготовленности студентов к тестированию. Если студенты не подготовлены или материал не из их «зоны ближайшего развития», то, как показывают экспериментальные данные, случайная величина X будет распределена по нормальному закону (белый шум с распределением Гаусса).

На рисунке 1 через M ₁, M ₂, М ₃ обозначены значения математических ожиданий случайной величины Х в зависимости от подготовленности студентов.

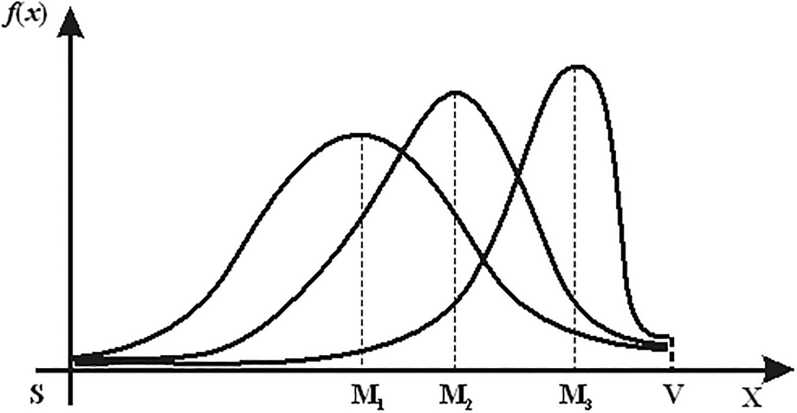
Рис. 1. Изменение закона распределения Х в зависимости от подготовки

На основе статистического материала установим закон распределения случайной величины X . Для этого на специально сформированной шкале (рис. 2) отложим продолжительности реакций всех студентов в группе.

Для идентификации (определения) закона распределения рассмотрим экспериментальные данные, которые сформировались в системе MOODLE в течение 10 лет. В эксперименте участвовало 50 групп. Средняя численность студентов в одной группе 25 человек. Усредненные данные представлены на рисунке 3.

Ниджрес Моатаз Талал. Модель организации процесса тестирования    157

CR – продолжительность (быстрота) реакции

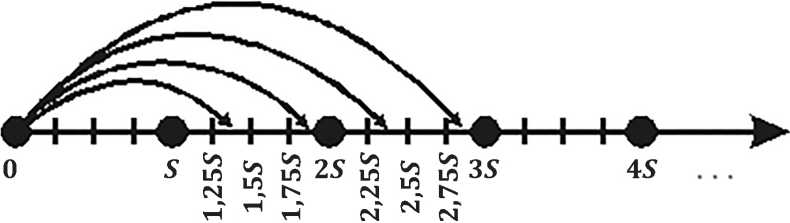
Рис. 2. Шкала для изменения быстроты (продолжительности) реакции студента

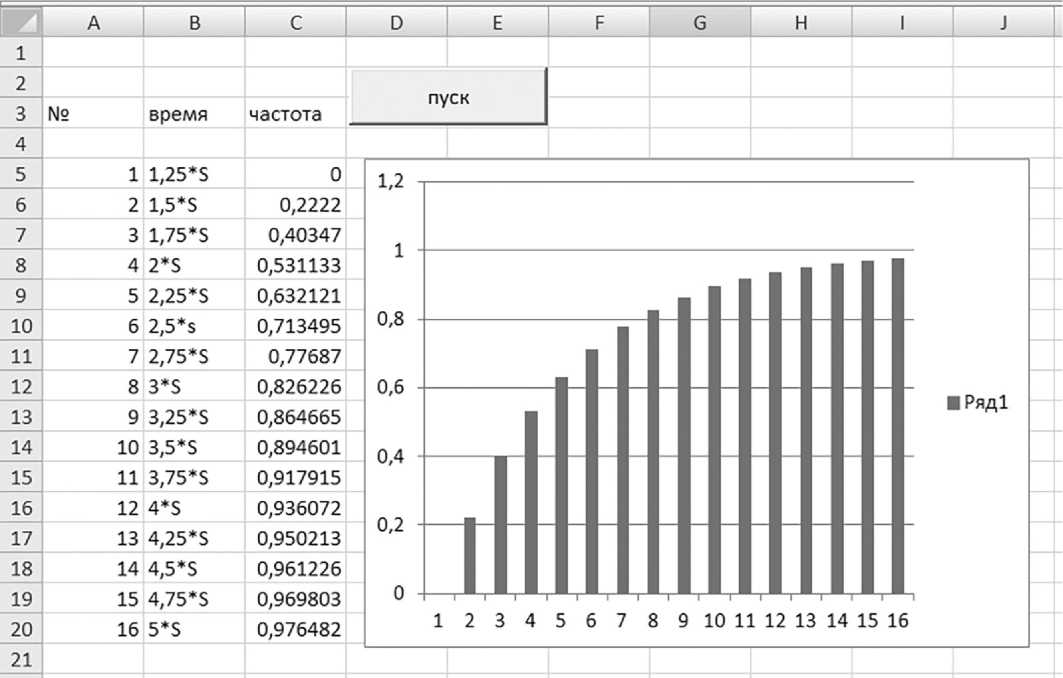
Рис. 3. Результат обработки экспериментальных данных (эмпирический закон распределения величины X )

Согласно данным графика частота (эмпирические вероятности) добровольного выхода студента из процесса (процедуры тестирования) будут следующие ( X – случайная величина – время выхода по завершению теста).

P ( X < 1,25 S ) = 0, т.е. вероятность того, что студент завершит тестирование раньше, чем 1,25 S , равна нулю, где S – сложность теста.

P ( X < 1,5 S ) = 0,2222, т.е. вероятность того, что студент завершит тест и выйдет с процесса тестирования раньше, чем 1,5 S , равна 0,22 (22%).

Аналогично: P ( X < 1,75 S ) = 0,40; P ( X < 2 S ) = 0,51, т.е. ко времени 2 S , завершив процесс, выйдет больше половины студентов и т.д.

Из графика следует, что активный выход студентов по завершении теста (продолжительность самообслуживания) начинается с момент времени S и продолжается до момента V (где V – конец тестирования). Исходя из этого начало координат на графике можно перенести на момент S , так как до момента S никто не завершает тестирование (см. рис. 4). Как следует из частотной характеристики случайной величины X (интегральная характеристика), средняя продолжительность самообслуживания (тестирования) в активной зоне равна величине Т (ср) = S .

158 в ыпуск 3/2020

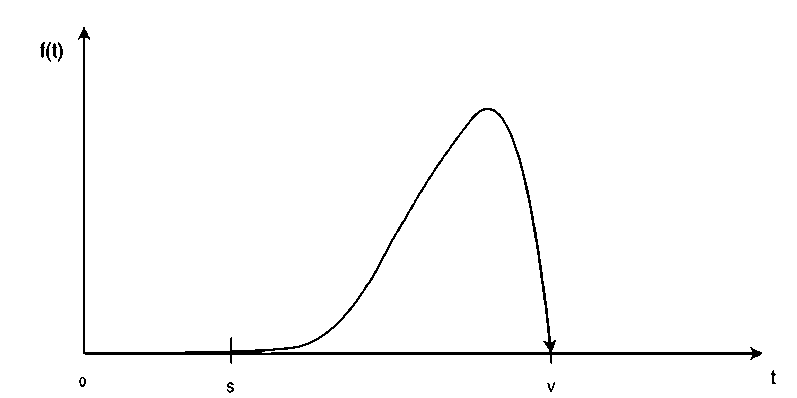
Рис. 4. Вид функции плотности вероятности случайной величины Х

Из статистического анализа данных (см. рис. 3) следует, что при уровне значимости α = 0,05 (гипотеза проверялась по критерию c ² ) случайная величина X подчиняется экспоненциальному закону распределения с интенсивностью потока λ = 1/ Т (ср) = 1/ S , т.е.

F ( x )

= <

—X x — e

0,

x >  0

x <  0

Из этого следует, что поток самообслуживающихся студентов является пуассоновским потоком.

Из тех же рассмотренных экспериментальных данных известно, что в среднем из группы с 25 студентами тест на положительную оценку не могут сдать 3,5 студента, и это независимо от продолжительности времени V . В целом это означает, что в среднем примерно 14% студентов сдают тест на оценку «два». Исходя из этой информации и данных графика находим, что V = 3 S .

Таким образом, если, по мнению эксперта, у теста как инструментального средства показатели U = E = 1, то ошибка оценки качества усвоенных знаний студента при продолжительности тестирования V = 3 S не превышает 5%, где S – сложность (трудоемкость) теста. Этот результат формально можно записать как D Z = abs( Z 1– Z ) ≤ 0,05, т.е. на практике надежность показателя Z 1 как оценки теста не менее 95% [1; 2; 4].

Тест на полноту содержит вопросы теоретического характера: определения, свойства, методы вычисления соответствующих характеристик, приложения. Соответственно, независимо от продолжительности тестирования V , оценка за тест полностью зависит от степени подготовленности студента. Понятно, что многие студенты, даже выполнив все задания, не покидают аудиторию до окончания тестирования (параметр V ). Однако неподготовленным студентам выделенного для ответов времени всегда будет недостаточно.

Цель данной работы – обосновать выбор времени V , так как излишнее увеличение времени тестирования не приведет к улучшению качества ответов студентов.

Результаты исследования и их обсуждение

Выполнен значительный объем наблюдений при проведении тестирования со студентами Института нефти и нефтехимии по следующим разделам курса высшей математики: линейная и векторная алгебра, аналитическая геометрия, дифференциальное

Ниджрес Моатаз Талал. Модель организации процесса тестирования 159 и интегральное исчисления функции одной переменной, комплексные числа, дифференциальные уравнения. Полученные результаты дают основание считать, что продолжительность тестирования не должна превышать величины 3S, а функция плотности вероятности распределения времени тестирования имеет вид, представленный на рисунке 4 ( V = 3 S ) [3; 5].

В таблице 2 представлен статистический ряд данных на полноту усвоенных знаний по архитектуре информационных систем (объем выборки n = 46).

Таблица 2

Наблюдаемые частоты, полученные в ходе тестирования

Номер интервала, i	Интервал, S	Частота, ni
1	[1; 1,25)	0
2	[1,25;1,5)	4
3	[1,5; 1,75)	3
4	[1,75; 2)	8
5	[2; 2,25)	9
6	[2,25; 2,5)	10
7	[2,5; 2,75)	4
8	[2,75; 3)	6
9	[3; 3,25)	3

Описание зависимости, представленной на рисунке 4 и, соответственно, в таблице 2, достаточно сложно, поэтому предлагается другой путь, более простой в реализации и интерпретации результатов, а именно: вводится линейная функция вида t = V - t , представляющая собой преобразование координат. При этом начало координат переносится в точку t = V , ось абсцисс меняет свое направление на противоположное, а величина t , имея смысл обратного времени, показывает, сколько времени осталось до конца тестирования. Точка S оси t отображается на оси t в точку V – S . Полигон относительных частот «обратного времени» представлен на рисунке 5 [3; 5], вариационный ряд – в таблице 3.

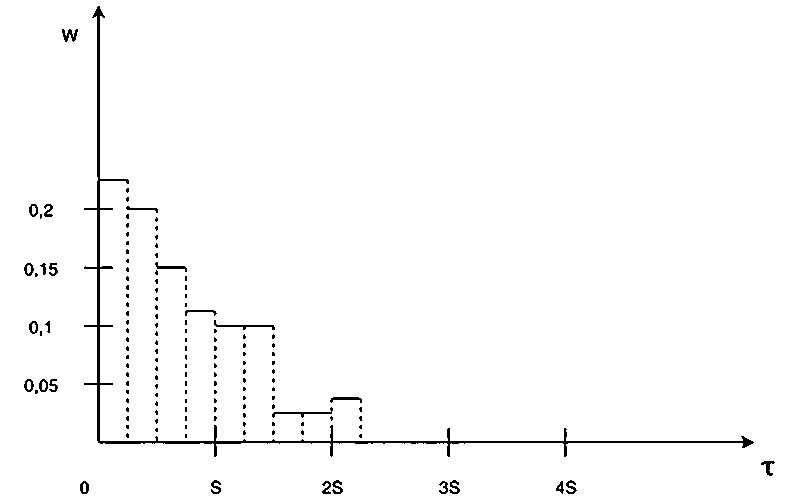
Рис. 5. Полигон относительных частот «обратного времени»

160 в ыпуск 3/2020

Таблица 3

Вариационный ряд «обратного времени»

Номер интервала	1	2	3	4	5	6	7	8	9
Интервал «обратное время», τ ( S )	(N о 5	Г4	сГ					г?	Г4 Л
Частота, n i	6	4	10	9	8	3	4	0	3

Функция плотности вероятности распределения «обратного времени» g(τ) с достаточной степенью точности аппроксимируется кривой, приведенной на рисунке 6, описание которой задается однопараметрической функцией g (т) =

Z e ^лт, T> 0,

0, т< 0,

где λ интертерпретируется как интенсивность выхода студентов по окончании выполнения тестовых заданий и определяется как величина, обратная среднему времени тестиро- вания, т.е. Z =

Xb (т) ■

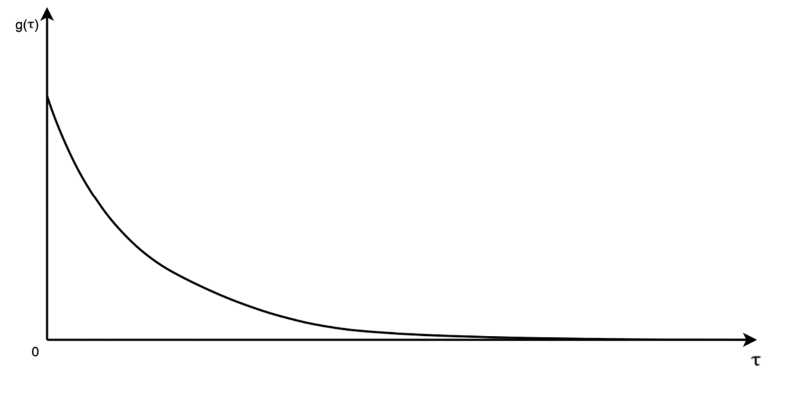
Рис. 6. Вид функции плотности вероятности распределения «обратного времени»

Определение экспертного времени S не вызывает затруднений и является, как правило, достаточно надежной величиной. Значение интенсивности λ как величины, обратной среднему времени тестирования, не обладает подобной устойчивостью, поскольку степень готовности студентов к тестированию различна. Проверим гипотезу о том, что время, оставшееся до конца тестирования, при уровне значимости 0,05 распределено по показательному закону, т.е. функция g (τ) = λ e ^–λτ может быть использована для описания данной величины (случайная величина t – «обратное время»). Проверку выполним по классическому критерию согласия c ² [5]. Результаты вычислений сведены в таблицу 4.

Ниджрес Моатаз Талал. Модель организации процесса тестирования 161

Таблица 4

Наблюдаемые и теоретические частоты, полученные в ходе эксперимента

№ интервала, i	n i	n* i	( n i- n i ) 2 ni
1	6	11,421	2,573
2	4	8,601	2,461
3	10	6,58	1,778
4	9	4,935	3,348
5	8	3,76	4,781
6	3	2,82	0,011
7	4	2,162	1,562
8	0	1,645	1,645
9	3	1,222	2,587
	47	43,146	χнабл= 20,746

Теоретические значения частот n_i ΄ вычисляются по формуле n_i^* = nP_i , где n – объем выборки; P_i – относительная частота соответствующего разряда экспоненциальной функции g (т) = Те - ^Хт ; для нахождения выборочной средней х в в качестве i -го интервала принималась его середина: x * = ( t+t i + 1 ) / 2 - выборочная средняя, где х * - середина интервалов (см. табл. 4).

x_B (6×0,125 + 4×0,375 + 10×0,625 + 9×0,875 + 8×1,125 + 3×1,375 + 4×1,625 +

+ 0×875 + 3×2, 125)/47 = 0,901 ;

Λ = 1/ x_B 1/ 0,901 = 1,11 .

Таким образом, дифференциальная функция предполагаемого показательного распределения имеет вид g ( т ) = 1,11 e ^{1,11 т} t >  0).

Вероятности попадания t в каждый из интервалов P i = e ^ i — e ^^T i ^{+ 1} :

P 1 = P ( 0 < T< 0,25 ) = e ^{— 1Д1} ' 0 — e ^{— 1,11} ' ^0, 2 ⁵ = 1 — 0,757 = 0,243.

P 2 = - ^{- 1} 'ⁿ' ⁰'²⁵ - e - 1'¹¹ ' ⁰'⁵ = 0,757 - 0,574 = 0,183,

P ₃ = 0,14 P ( 0,5 < T <  0,75 ) , P ₄ = 0,105 P ( 0,75 < T< 1 ) ;

P ₅ = 0,08 P ( 1 1,25 ) , P ₆ = 0,06 P ( 1,25 1,5 ) ;

P ₇ = 0,046 P ( 1,5 1,75 ) , P ₈ = 0,035 P ( 1,75 2 ) ;

P 9 = 0,026 P ( 2 2,25 ) .

Теоретические частоты n_i^* = 43,146 P_i ; n ₁ ^* = 11,421; n ₂ ^* = 8,601; n ₃ ^* = 6,58; n ₄ ^* = 4,935; n ₅ ^* = 3,76; n ₆ ^* = 2,82; n ₇ ^* = 2,162; n ₈ ^* = 1,645; n ₉ ^* = 1,222.

Определяем значение критерия Х ^абл по формуле

n

Х набл    ^^

( n_i

—

*

i = 1

ni

= 20,746.

162 в ыпуск 3/2020

По таблице критических точек распределения c ² , по заданному значению α = 0,05 и числу степеней свободы k = s – 2 = 9 – 2 = 7 находим c ² _крит= c ² (0,05; 7) = 14,1.

Так как χ ² _nabl <  χ ² krit , то нет оснований отвергнать гипотезу о показательном распределении «обратного времени».

Заключение

Таким образом, из результатов исследований следует, что при выполнении всех перечисленных условий к тесту как измерительному средству педагог должен действовать по следующему алгоритму.

• 1.    Убедиться, что качество содержания теста как измерительного инструмента соответствует норме.

• 2.    Эксперт (педагог) должен оценить S – сложность (трудоемкость в мин/раб.) теста.

• 3.    Задать для студентов продолжительность (трудоемкость) тестирования V = 3 S (мин/ра.).

• 4.    Провести процедуру тестирования.

Как показывает опыт, полученную эвристическую формулу V = 3 S , т.е. обоснованную продолжительность тестирования, можно использовать только в ограниченном диапазоне изменений S . Экспериментально установлено, что этот диапазон равен 0 <  S ≤ 20 мин. При больших значениях S , т.е. S > 20, погрешность оценки результата D Z достаточно быстро возрастает, а это означает, что точность тестирующей системы падает. По гипотезе авторов, которая многократно проверялась, появляется новый фактор – усталость студента.

В общем случае в результате системного анализа было установлено неравенство Стну-пе V – S > 2 Т (ср), определяющее количественное соотношение между величинами Т (ср), V , S , которое можно использовать на практике; например, при известных Т (ср) S позволяет установить наименьшее допустимое значение продолжительности тестирования V . В частности при Т (ср) = S получаем ранее приведенное правило V = 3 S .