Модель плазменного нагрева композиции «металлизационное покрытие - основа»

Белинин Дмитрий Сергеевич, аспирант затрудняется его пористой структурой и отсутствием данных о теплофизических характеристиках большинства применяемых для напыления материалов. Наибольший интерес представляет знание температуры границы «покрытие-подложка», так как большой перепад температур в данной зоне может привести к отслоению покрытия.

Цель работы: определение распределения температур в композиционном материале «металлическое покрытие-основа» для оптимизации режимов плазменной обработки металлизацион-ных покрытий на основе железа.

Для решения поставленной задачи построим математическую модель процесса распределения температур в композиционном материале на основе решения краевой задачи теплопроводности в пакете MathCad 14. Композицию «покрытие-основа» будем считать пластиной с переменными по толщине теплофизическими свойствами (рис. 1).

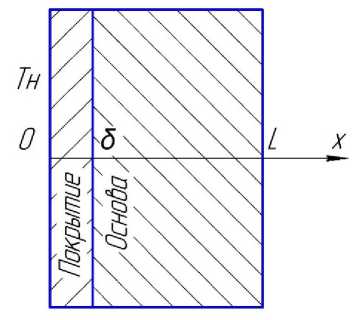
Рис. 1. Схема задачи

Математическая постановка задачи теплопроводности для одномерного поля температур имеет вид:

9T_t    . d ² T             „

C 1 P1-57 =       ,⁰< x < 8

dT2    3 d2T2 -          ,

C z Pz^ = X z— ,S <  ^x < L

I

С учетом пористости покрытия эффективные объемная теплоёмкость и теплопроводность материала примут следующий вид [6]:

cp = ^c м p м ⁽¹ - P) + с в p в P ;

1    11-P pp

X = Xм X в , где см pм, с в p в - объёмная теплоёмкость материала покрытия и воздуха в порах; Xм, X в -теплопроводность материала покрытия и воздуха в порах; P – пористость покрытия (в зависимости от напыляемого материала и параметров режима дуговой металлизации может изменяться от 2 до 12% [7]).

Так как теплофизические характеристики металлизационных покрытий из порошковых проволок различного состава не известны, то их расчет будем выполнять в зависимости от процентного содержания легирующих элементов [8] по формулам (2), и будем считать их независящими от температуры.

Л = 20(11 - 7v^) ; cp = 10(55 - 9V°), где σ – коэффициент зависящий от содержания легирующих элементов

° = 4

3 (^с+5 (^{№+ со + си +}у))⁺

Мп Si + Al Ct + V + Ti Мо + Nb + Zt

V U+  "+   13   +    24   /

Как показано в работе Стрельцова Ф.Н. [9], температура поверхности в зоне воздействия плазменной дуги сильно зависит от её параметров и изменяется в диапазоне от 2100 до 2500ºС. Таким образом, температуру поверхности покрытия под воздействием сжатой дуги будем считать известной, и зададим её граничными условиями I рода.

T = T_w(x, t) ,           (3)

где T_w (x, t) - температура на поверхности тела.

Для определения теплового взаимодействия между элементами с различными теплофизическими характеристиками на границе «покрытие – основа» зададим граничные условия IV рода [10].

I

T 1 (x, t) = T₂(x, t) .. дт1 _ ₃ dT ₂

■ ^X1 дх = ^X 2 дх

Будем считать, что обрабатываемая пластина с покрытием лежит на поверхности, плохо проводящей тепло, то есть тепловой поток в ограждающую конструкцию равен нулю.

-X^ T = 0

² дх

Для решения дифференциального уравнения теплопроводности в частных производных воспользуемся методом конечных разностей, то есть аппроксимируем (1) их конечно-разностными аналогами.

гр 71+1 ^Ip.       /грП+l o+n+l,+n+l\ cp Tl--Tl- = X (T+1 "2T-2 +T'-1 ),   (6)

где T-¹ - температура в i-ом (i = 0^ N) узле в момент времени n, h, τ – шаг по координате и времени, соответственно.

Полученную систему можно свести к виду трехточечного уравнения второго порядка:

A - T^¹ - B i T ^ ⁺¹ + C_iT' -+ = F_t ,     (7)

где At = Ct =   ; Bl = 20 + EP ; f = - 2^ T ”

h2          h2T              т

Предположим, что существуют такие наборы чисел α i и β i , тогда трехточечное уравнение второго порядка можно преобразовать в двухточечное уравнение первого порядка:

T -+ ¹ = « i T^¹ + P t        (8)

Подставив уравнение (8) в уравнение (7) получаем:

_Tn+1 =      ^A i    _Tn+1 ₊ ^C i ^p t-1 ^{- A} i

• ^{1       B} i ^{- C} i ^a i-1 ^{i+1 B} i ^{- C} i ^a i-1

откуда получаем так называемые прогоночные коэффициенты α i и β i :

« = ^Ai ' В = C i P i-X -A i .

• ^{- B}i ^{- C}i « i-1 ’ ^{1 B}i^{- C}i « i-1

Чтобы определить α i и β i необходимо знать α 0 и β 0 , которые находятся из левого граничного условия (3). Найдя все прогоночные коэффициенты и определив из правого граничного условия (5) температуру T N можно рассчитать неизвестные T F ⁺¹.

Покрытие толщиной 2 мм нанесено на подложку из низкоуглеродистой стали 20 толщиной 10 мм. В качестве материала для нанесения покрытия была использована порошковая проволока ППМ-6 системы легирования 150Х8Т2Ю [11]. Для определения влияния режимов плазменного воздействия и характеристик покрытия на распределение температур в композиции «покрытие-основа» проведен ряд экспериментов (табл. 1). Результаты проведенных экспериментов представлены на рис. 2.

Таблица 1. Режимы экспериментов

№ опыта	Пористость, %	Температура подогрева, °С	Температура нагрева (режим обработки), °С	Время воздействия, с
1	P1 = 2; P2 = 6; P3 = 10	0	2300	6
2	6	Tp1 = 0; Tp2 = 150; Tp3 = 300	2300	6
3	6	0	Tn1 = 2100; Tn2 = 2300; Tn1 = 2500	6
4	6	0	2300	t1 = 2; t2 = 6; t3 = 10

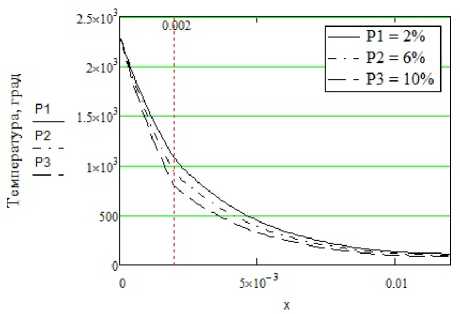
Толщина пластины, м

а)

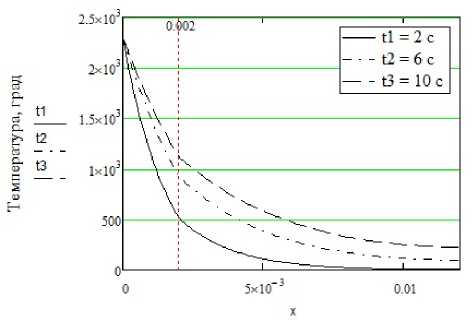
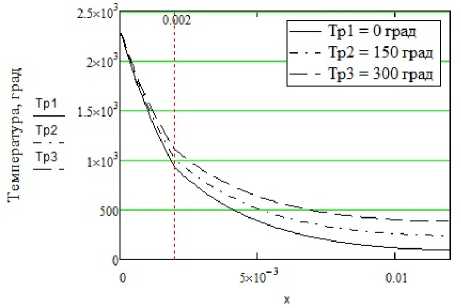
Толщина пластины, м

толщина пластины, м г)

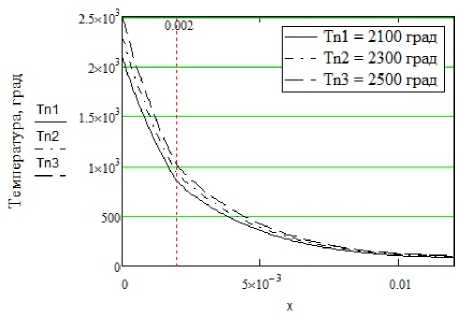
Рис. 2. Графики распределения температур в зависимости от: а) пористости покрытия, б) температуры подогрева, в) температуры нагрева, г) времени воздействия источника

б)

Толщина пластины, м в)

На рис. 2,а видно, что чем больше пористость, тем меньше интенсивность нагрева покрытия, что связано с низкой теплопроводностью воздуха в порах. Таким образом, пористость покрытия значительно усложняет процесс плазменной обработки композиционного материала. Повышение температуры предварительного подогрева (рис. 2,б), температуры нагрева поверхности изделия (рис. 2,в), регулируемой параметрами режима сжатой дуги, и времени воздействия источника на поверхность (рис. 2,г) позволяют повысить температуру на границе «покрытие-основа». Таким образом, для предотвращения отслоения покрытия вследствии больших перепадов температуры в переходной зоне может потребоваться предварительный подогрев композиции, а также повышение погонной энергии плазменной обработки.

Выводы: разработана математическая модель плазменной поверхностной обработки композиции «металлизационное покрытие-основа». Полученные графики распределения температур позволяют дать рекомендации по оптимизации параметров плазменной обработки, а также оценить характер влияния пористости и состава покрытия на распределение температур в композиции под воздействием сжатой дуги.