Модель построения рейтинга сотрудников КНИТУ-КАИ на основе прокси-показателя научной продуктивности

Автор: Румянцев Алексей Александрович, Хабибулин Ринат Рахимович, Александров Александр Сергеевич

Журнал: Образовательные технологии и общество @journal-ifets

Статья в выпуске: 3 т.22, 2019 года.

Бесплатный доступ

Исследована существующая перспективная математическая модель индикатора относительной научной продуктивности Джованни Абрамо. Проанализированы результаты ее применения и дана оценка адекватности при расчете рейтинга научных сотрудников кафедры АСОИУ КНИТУ-КАИ. Разработаны модификации на основе детализации отдельных показателей, ввода дополнительных параметров оценки работ авторов, цитирований из журналов и использования экспертных средств нормализации количественных показателей. Произведено сравнение эффективности полученной модели с ранее достигнутыми результатами.

Показатель относительной научной продуктивности, рейтинг публикационной активности, математическая модель, мягкие вычисления

Короткий адрес: https://sciup.org/140245474

IDR: 140245474

Текст научной статьи Модель построения рейтинга сотрудников КНИТУ-КАИ на основе прокси-показателя научной продуктивности

Важной задачей в современном глобализированном мире является оценка результативности научной деятельности с целью повышения эффективности и продуктивности научной и технологической инфраструктуры. Существует большое многообразие программ оценивания, рейтингов научной деятельности на государственном и международном уровнях. Однако значительная их часть опирается на ненаучные, интуитивные, упрощенные методики оценивания, неадекватные с микроэкономической точки зрения [1]. Грамотный подход к оценке продуктивности научного работника опирается на действительно значимые количественные факторы. Такие показатели содержатся в различных библиографических базах данных, таких как РИНЦ, Scopus, Web Of Science и др [2]. Данные сервисы обладают очень ограниченным функционалом при формировании рейтинга авторов, но содержат большие массивы данных для множества библиометрических индикаторов, что позволяет производить полноценную статистическую оценку на основе индивидуальных работ каждого автора [3, 4]. Необходимость применения интегрированной оценки вклада каждого научного работника в “экономику, основанную на знаниях”, а также описание алгоритма расчета рейтинга и математической модели на ее основе отражено в ранее проведенных исследованиях [5, 6].

Разработка эффективной математической модели требует тщательных исследований адекватности ее применения при различных факторах и алгоритмических параметрах [7]. В качестве решения данной задачи нами дана оценка для некоторых базовых методов построения рейтинга публикационной активности на основе разработанного программного обеспечения [8]. Были определены эффективные методы математического аппарата [9], в частности на основе преобразований мягкими вычислениями, а также предложена идея учета индикаторов популярности и дециля работ авторов (Новые тезисы). Однако ограниченность библиометрических показателей разновидностями индекса Хирша не учитывает влияние научных работ с количеством цитирований менее h -индекса и количество цитирований основных работ ( h ), превышающее h [10]. Кроме того, h -индекс не предусматривает нормализации количества цитирований и интенсивности цитирований по предметной области и не учитывает количество соавторов. С целью устранения данных недостатков нами предложено использование существующей достаточно адекватной экспериментально проверенной модели – показателя относительной научной продуктивности (Fractional Scientific Strength), предложенного командой исследователей под руководством Джованни Абрамо [11]. Данная модель представлена в упрощенной форме, что открывает возможности для ее модификации различными математическими средствами для детализации, нормализации и учета дополнительных индикаторов. Результаты применения сформированной модели могут быть представлены и проанализированы в виде итоговой оценки или на различных временных промежутках в соответствии с рекомендациями разработчиков исходной модели.

Показатель относительной научной продуктивности

Математическая интерпретация исходной модели Fractional Scientific Strength представлена следующей формулой:

FSS_r = ——У =ft

Wr tR 4-* c i=1

Где:

FSS_R - показатель относительной научной продуктивности,

WR - среднегодовая заработная плата ученого, tR - количество лет работы ученого в рассматриваемом периоде, ct - количество цитирований на публикацию i,

С - среднее значение распределения цитирований всех процитированных работ в том году и тематической области, к которой относится публикация i , f t - относительный вклад ученого в подготовку публикации i .

Данные показатели представлены в библиографических базах данных, статистических центрах обработки экономических показателей и нормативно-правовых документах в открытом доступе [12]. Среднегодовая заработная плата рассчитывается на основе официального положения об окладах для КНИТУ-КАИ с учетом надбавок в зависимости от должности и ученого звания сотрудника [13]. Параметры периода публикации и окна цитирования с отсчетом от момента регистрации публикации определяются на основе рекомендации разработчиков исходной модели как 3 года для наибольшей адекватности и точности [14, 15].

Временной интервал применения процедуры рассчитывается с первой публикации. Нормализация рейтинга проводится в пределах одной модели.

База данных

Применяемая база данных (рис. 1) основана на библиометрических показателях 700 публикаций и статистике заработных плат с учетом инфляции 21 сотрудника кафедры автоматизированных систем обработки информации и управления (АСОИУ) Казанского национального исследовательского технического университета им. А.Н. Туполева–КАИ, а также позиции в рейтинге Science Index цитирующих журналов (107 журналов, 401 отношение).

Идентифкатор ФИО	Зарплата Код публикации		Цитирования	Норм цит. Дециль Просмотры			Загрузки
603113 Барков Игорь Александрович	39910	19565261	10	1.397	2	1	0
759697 Валов Олег Павлович	35000	25700653	7	0.524	3	6	0
775383 Вафин Радик Рашитович	25150	17846862	1	0.398	4	4	1
2500 Галеев Ильдар Хамитович	35000	15189748	47	26.79	1	72	49
845002 Зайнуллина Гульсина Рафкатовна	22950	23437628	18	11.48	1	33	23
325092 Зарайский Сергей Александрович	35000	20274188	3	2.304	1	23	13
773327 Захарова Земфира Хаматовна	25150	17642226	10	5.177	1	18	9
699483 Медведев Михаил Викторович	35000	22909962	22	4.187	1	13	1
706627 Мокшин Владимир Васильевич	35000	22020910	61	28.79	1	41	24
958965 Осипова Алла Леонидовна	25150	17346398	14	6.066	1	20	12
846704 Ризаев Ильгизар Султанович	35000	25999726	17	3.436	1	12	5
697909 Ризаев Ильдус Султанович	35000	17346398	14	6.066	1	20	12
808683 Суздальцев Владимир Антонович	25150	27581508	5	674	1	3	0
749257 Сытник Анатолий Сергеевич	35000	21022604	2	0.924	3	13	6
449014 Тахавова Эльза Габдулбаровна	35000	22724767	3	2.113	2	2	0
760474 Хохлов Дмитрий Григорьевич	35000	17642226	10	5.177	1	18	9
478213 Шарнин Леонид Михайлович	43222	20294476	60	25.07	1	27	14
700796 Шлеймович Михаил Петрович	43050	22909962	22	4.187	1	13	1
722166 Эминов Фарид Ибрагимович	35000	26064966	19	6.23	1	99	30
745736 Якимов Игорь Максимович	35000	22020910	61	2879	1	41	24
490313 Яхина Зухра Талгатовна	35000	23437628	18	11 48	1	33	23

Рис. 1. База данных сотрудников кафедры АСОИУ

Детализация и дополнение модели Fractional Scientific Strength

Исходная модель, предложенная Джованни Абрамо, обладает определенными недостатками из-за ограниченности учета экономических факторов и количественной нормализации параметров, а также применения только одного критерия оценки работ автора. В качестве усовершенствования исходной модели с целью устранения выявленных недостатков нами предложены следующие решения:

• Учет годовой инфляции [16], хронологии получения ученых степеней и статистики заработных плат в сфере высшего образования службы Росстата [17], применимой к окладам КНИТУ-КАИ;
• Ввод показателей количества просмотров и загрузок работ зарегистрированными пользователями в качестве нормализованного экспертного суммирования вместе с оценкой цитирования;
• Применение мягких вычислений на основе экспертно формируемой функции принадлежности и степенной функции для нормализации показателей публикаций;
• Учет распределения цитирований по тематике публикации на основе дециля цитирований;
• Применение параметра позиции в рейтинге Science Index [18] для цитирований из журналов;

Таким образом, становится возможным повысить точность и адекватность модели, а также в большей степени учитывать значимость работ автора. Итоговая математическая формула для модифицированной модели:

N h-\

^У^ + ^^ + ^З71^

fssr = ^r™^(kici(i + k4Rsi,i)(1 — k

R R i=i

Где

С>к=1

FSS_r - модифицированный показатель относительной научной продуктивности,

WR - среднегодовая заработная плата ученого с учетом статистики и инфляции, tR - количество лет работы ученого в рассматриваемом периоде, ci - исходное количество цитирований i-ой публикации, щ - нормализованное по среднему в тематике и максимальному значению среди авторов количество цитирований на публикацию i, hi - дециль в предметной области для публикации i, тщ - количество просмотров публикации i, щ - количество загрузок публикации i, k1, k2, k3, k4, k5, k6 - экспертные оценки для параметров, fi - относительный вклад ученого в подготовку публикации i, RSI l - интегрированный рейтинг SCIENCE INDEX l-ой публикации, Cj,ik - количество цитирований l-ой публикации из к-го журнала, Rj,k - позиция к-го журнала в рейтинге SCIENCE INDEX,

S - константа, 0.000283.

В рамках представленной работы использованы актуальные данные ежемесячной заработной платы работников высшего образования применительно к окладам КНИТУ-КАИ с учетом годовой инфляции (рис. 2). Для дальнейшей оценки также представлены хронологические данные публикационной активности наиболее активных авторов (рис. 3).

Год	1995	2000	2001	2002	2003	2004	2005	2006	2007	2008
Зарплата	455	1826	2699	4310	5369	6546	8503	10717	13868	16955
Инфляция	131.6	20.1	18.8	15	11.9	11.7	10.9	9	11.8	13.2
Год	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018

Зарплата 20214 21319 23180 26321 31666 35503 38185 41747 44972 48447

Инфляция 8.8 8.7 6.1 6.5 6.4 11.3 12.9 5.4 2.5 4.3

Рис. 2. Экономические показатели среднестатистической ежемесячной заработной платы и годовой инфляции

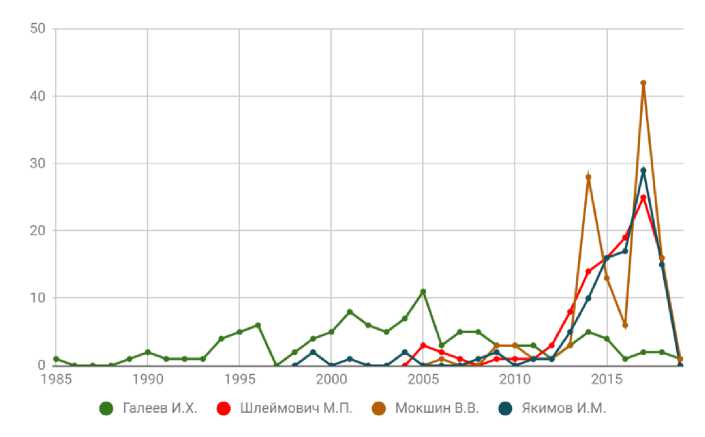
Рис. 3. Хронологическое распределение публикаций авторов

Мягкие вычисления

Применение нечеткой математики для нормализации количественных показателей просмотров и загрузок связано с неопределенностью, неточностью понятий при оценке значимости распределения данных [19]. Элементами мышления человека являются не числа, а элементы некоторых нечетких множеств. Данный подход позволяет более справедливо оценить каждый параметр при нормализованном экспертном суммировании. Графики и параметры сигмоидных функций принадлежности представлены на рис. 4.

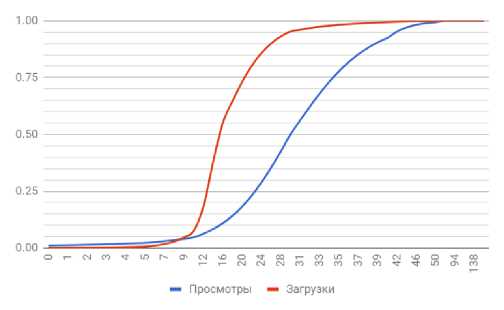
Рис. 4. Функции распределения нормализованных показателей

Сравнительный анализ результатов

Результаты применения исходной модели Fractional Scientific Strength для научных сотрудников кафедры АСОИУ КНИТУ-КАИ с целью анализа продуктивности при различных фиксированных периодах публикации и минимальном окне цитирования 3 года представлены на рисунке 5. Как видно наибольшей продуктивностью за все периоды обладает Галеев И.Х., хотя показатели Мокшина В.В., Якимова И.М. и других авторов также заметно растут, что говорит о высокой интенсивности недавней публикационной активности, актуальности и популярности работ авторов.

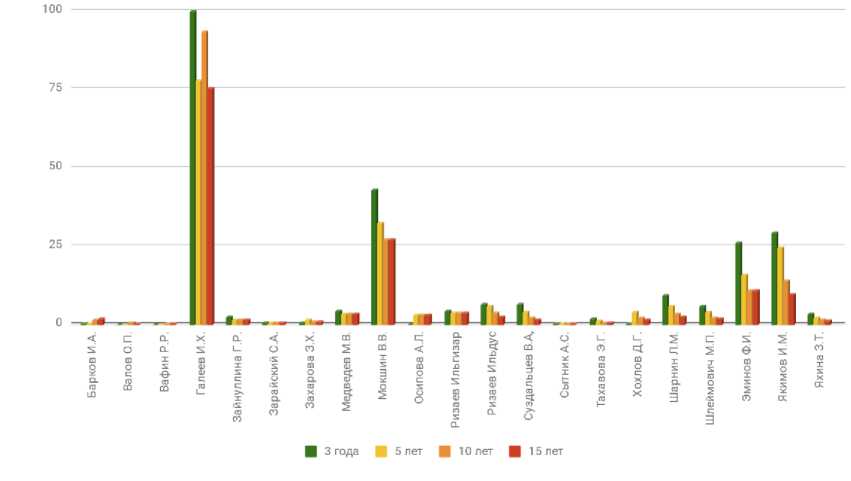
Рис. 5. Продуктивность авторов за разные периоды публикации (исходная Fractional Scientific Strength)

Таким образом, рассмотренная модель позволяет оценить актуальную продуктивность научного сотрудника для стимулирования качества научноисследовательской деятельности, эффективного распределения бюджетных ресурсов в условиях производственной конкуренции. Однако не менее важной задачей является справедливая интегрированная оценка общей результативности автора за весь период публикационной активности. Сравнение итоговых рейтинговых оценок ранее разработанных нами моделей на основе h-индекса и Fractional Scientific Strength с учетом модификаций при неограниченном окне цитирования приведено на рисунке 6. Как видно общая значимость работ Галеева И.Х. заметно превосходит остальных авторов на всем интервале публикационной активности. В сравнении с методом мягких вычислений на основе h-индекс модели общий прокси-индекс дает значительно более строгую оценку почти для всех авторов, опираясь только на нормализованное цитирование и не учитывая популярность работ по критериям просмотров и загрузок. Несколько более справедливую оценку для большинства авторов дает разработанная модификация исходной модели при базисных экспертных параметрах. Таким образом, необходим разносторонний учет значимости каждой работы автора.

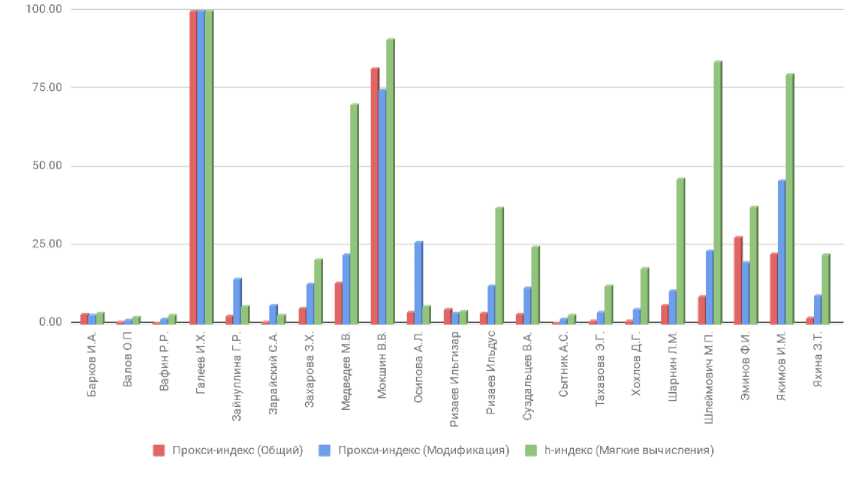
Рис. 6. Общая продуктивность авторов (Fractional Scientific Strength и h-индекс методы)

Применение детализированной и дополненной модели Fractional Scientific Strength требует экспертной оценки для подбора параметров к 1 , к₂, к₃, к₄, к₅, к₆ при суммировании, нормализации с , по децилю в предметной области и применении рейтинга Science Index для цитирований из журналов. Экспериментальный анализ различных вариаций данных параметров при общем рейтинге без учета периода публикации на основе базиса коэффициентов (0.5, 0.3, 0.2, 1, 0.8, 1.15) с учетом масштабирования весовых значений в общей сумме отображен на рис. 7.

ФИО	Базис	к1=0.15	к1=0.85	k2 0.15	k20.85	k3 0.15	кЗ=0.85	к4 0	к4=3	к5 0.01	кб0.99	ktiD.5	к6 10
Барков Игорь Александрович	0.75	1.02	0.48	0.53	1.55	0.79	0.30	0.75	0.75	0.77	0.75	0.71	0.77
Валов Олег Павлович	0.30	0.49	0.12	0.17	0.79	0.32	0.10	0.30	0.30	0.31	0.30	0.30	0.31
Вафин Радик Рашитович	0.2Б	0.14	0.38	0.28	0.16	0.28	0.05	0.05	0.69	0.26	0.26	0.26	0.2Б
Галеев Ильдар Хамитович	Б3.73	54.86	72.60	65.39	56.63	64.87	48.69	45.60	100.00	63.83	63.71	63.47	63.83
Зайнуллина Гульсина Рафкатовна	2.14	2.30	1.97	2.03	2.54	2.15	1.99	1.36	3.69	2.14	2.14	2.13	2.14
Зарайский Сергей Александрович	О.ББ	0.57	0.76	0.67	0.64	0.Б8	0.42	0.29	1.42	0.66	0.66	0.66	0.6Б
Захарова Земфира Хаматовна	3.33	2.03	4.64	3.56	2.35	3.51	1.02	1.35	7.30	3.34	3.33	3.32	3.34
Медведев Михаил Викторович	3.31	3.06	3.55	3.11	3.97	3.44	1.54	2.26	5.40	3.32	3.31	3.28	3.32
Мокшин Владимир Васильевич	13.98	11.34	16.62	14.14	13.02	14.46	7.68	11.4.9	18.96	13.98	13.98	13.97	13.98
Осипова Алла Леонидовна	3.89	4.09	3.69	3.83	4.13	3.87	4.10	2.29	7.10	3.89	3.89	3.89	3.89
Ризаев Ильгизар Султанович	0.50	0.65	0.34	0.36	0.98	0.52	0.19	0.50	0.50	0.50	0.4.9	0.48	0.50
Ризаев Ильдус Султанович	4.89	5.12	4.66	4.БЗ	5.85	4.96	4.06	2.95	8.78	4.90	4.89	4.87	4.90
Суздальцев Владимир Антонович	4.72	4.82	4.63	4.40	5.86	4.84	3.21	2.82	8.52	4.73	4.72	4.71	4.73
Сытник Анатолий Сергеевич	0.17	0.14	0.19	0.16	0.19	0.17	0.05	0.07	0.35	0.17	0.16	0.16	0.17
Тахавова Эльза Габдулбаровна	0.93	1.52	0.34	0.51	2.49	0.99	0.23	0.93	0.93	0.94	0.93	0.92	0.94
Хохлов Дмитрий Григорьевич	З.Б7	3.44	3.89	3.41	4.50	3.82	1.70	1.85	7.30	3.67	3.66	3.64	3.67
Шарнин Леонид Михайлович	4.91	3.84	5.99	5.06	4.23	5.07	2.81	2.85	9.03	4.92	4.91	4.90	4.92
Шлеймович Михаил Петрович	Б.81	6.84	6.77	6.10	9.24	7.10	3.08	4.41	11.60	6.82	6.80	6.77	6.82
Эминов Фарид Ибрагимович	4.71	6.72	2.70	3.65	8.69	4.75	4.40	4.71	4.71	4.72	4.71	4.69	4.72
Якимов Игорь Максимович	17.09	17.74	16.45	15.87	21.41	17.48	12.20	12.53	26.22	17.12	17.09	17.03	17.12
Яхина Зухра Талгатовна	3.72	4.30	3.14	3.39	4.97	3.74	3.48	2.55	6.07	3.72	3.72	3.71	3.72

Рис. 7. Таблица общего рейтинга при различных экспертных параметрах

(модифицированная Fractional Scientific Strength)

Анализ данной таблицы показывает значимость различных параметров для рейтинга отдельных авторов. В частности, сильное влияние нормализованного цитирования почти у всех авторов, 1.5-2 кратный рост за счет высокой суммарной популярности по количеству просмотров работ относительно общей выборки у многих авторов с невысоким рейтингом (Эминов Ф.И., Тахавова Э.Г.), сниженный рейтинг по количеству загрузок у большинства авторов, кроме Осиповой А.Л., и незначительно у Эминова Ф.И., Яхиной З.Т. Также наблюдается заметное влияние рейтинга цитирований из журналов Science Index. Коэффициенты при нормализации цитирований по децилю в предметной области оказывают незначительное влияние на общую картину для данной выборки по причине небольшого размера, статистических особенностей и отсутствия аномалий в общем распределении публикаций по тематикам, однако, как показано в работе Джованни Абрамо данный фактор может быть значимым при обработке больших разнотипных данных [13].

Хронологические результаты применения исходной и модифицированной модели Fractional Scientific Strength при различных периодах публикации с минимально необходимым окном цитирования 3 года при точке отсчета от даты публикации и базисными экспертными параметрами для наиболее цитируемых авторов отображены на рис. 8, 9.

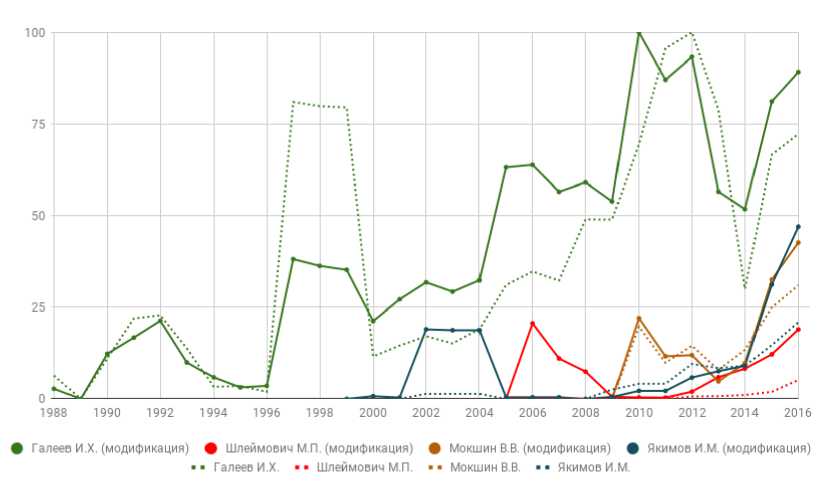
Рис. 8. Хронологическая продуктивность авторов (период публикации 3 года)

На графиках можно заметить значительное превосходство интервального рейтинга Галеева И.Х. на всем анализируемом отрезке с резким ростом локальной продуктивности Якимова И.М. и Мокшина В.В. за последние 2-3 года. Модифицированная модель показывает более сглаженную оценку на множестве пиковых значений, меньший относительный разброс значений и большую чувствительность к значимости публикаций, что точнее и справедливее описывает результативность научно-исследовательской деятельности автора при заданном периоде публикации. Таким образом, сформированная модель является более эффективной при интервальном и общем анализе научной продуктивности.

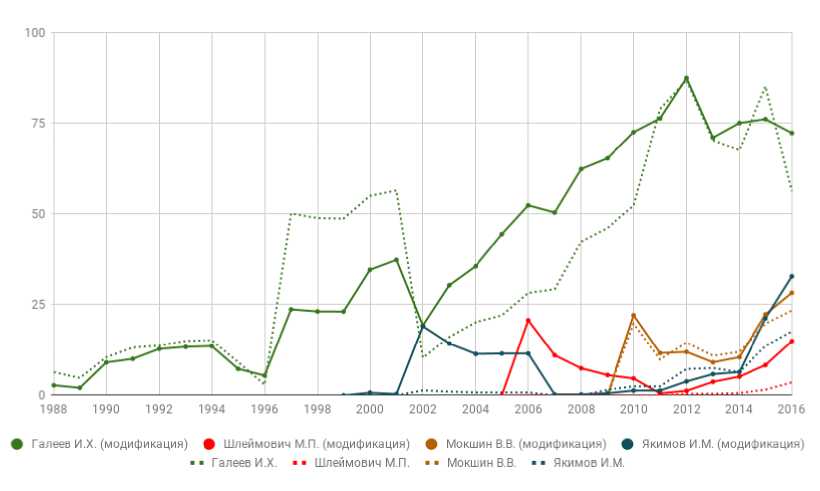
Рис. 9. Хронологическая продуктивность авторов (период публикации 5 лет)

Заключение

В процессе исследования различных математических подходов формирования рейтинга публикационной активности были выработаны перспективные решения, примененные на основе показателя относительной научной продуктивности для оценки общей и интервальной результативности научных сотрудников кафедры АСОИУ КНИТУ-КАИ. Показана эффективность детализированной и дополненной модели Fractional Scientific Strength в сравнении с исходной и ранее разработанными методиками при различных экспертных параметрах и периодах публикации.

Работа выполнена под научным руководством доцента кафедры АСОИУ КНИТУ-КАИ Галеева Ильдара Хамитовича.

Список литературы Модель построения рейтинга сотрудников КНИТУ-КАИ на основе прокси-показателя научной продуктивности

Abramo G. Bibliometric evaluation of research performance: where do we stand? Voprosy Obrazovaniya/Educational Studies Moscow, 2017, no 1, pp. 112-127.
Галеев И.Х. Научный журнал в информационном пространстве // Высшее образование в России. - 2009. - № 3. - С. 92 - 95.
Галеев И.Х. Оценка полноты и интеллектуальности РИНЦ // Международный электронный журнал "Образовательные технологии и общество (Educational Technology & Society)" - 2014. - V.17. - №3. - C. 583-602. - ISSN 1436-4522.
Каленов Н.Е., Селюцкая О.В. Некоторые оценки качества Российского индекса научного цитирования на примере журнала «Информационные ресурсы России» // Информационные ресурсы России. - 2010. - № 6. - С. 2-13.
Галеев И.Х. Практика применения баз данных научного цитирования при оценке публикационной активности КНИТУ // Международный электронный журнал "Образовательные технологии и общество (Educational Technology & Society)" - 2013. - V.16. - №4. - C. 387-402. - ISSN 1436-4522.
Галеев И.Х., Галеева Н.Х. Опыт анализа публикационной и издательской активности с использование РИНЦ // Международный электронный журнал "Образовательные технологии и общество (Educational Technology & Society)" - 2012. - V.15. - №1. - C.594-608. - ISSN 1436-4522.
Галеев И.Х. Информационно-образовательное пространство России и «перечень» журналов // Высшее образование в России. - 2009. - № 10. - С. 15 - 23.
Румянцев А.А., Хабибулин Р.Р., Александров А.С. Автоматизация проектирования рейтинга научных сотрудников КНИТУ-КАИ // САПР и моделирование в современной электронике: сб. науч. тр. II Международной научно-практической конференции. - Брянск: БГТУ, 2018. - Ч.2. - С.39-41.
Румянцев А.А., Хабибулин Р.Р., Александров А.С. Разработка среды автоматизированного проектирования рейтинга научных сотрудников КНИТУ-КАИ // "Образовательные технологии и общество" - 2019. - V.22. - №1. - С.11-24. - ISSN 1436-4522.
И.Х. Галеев Динамика развития международного электронного журнала "Образовательные технологии и общество" // Международный электронный журнал "Образовательные технологии и общество (Educational Technology & Society)" - 2007. - V.10. - №1. - C.315-328. - ISSN 1436-4522.
Abramo G., D’Angelo C.A. How Do You Define and Measure Research Productivity? Scientometrics, 2014, vol. 101, no 2, pp. 1129-1144.
Румянцев А.А., Хабибулин Р.Р., Александров А.С. Формирование интегрированного рейтинга публикационной активности преподавателей КНИТУ-КАИ // Актуальные проблемы науки в студенческих исследованиях: сборник материалов VIII Всероссийской студенческой научно-практической конференции. - Альметьевск. - М.: Издательство «Перо», 2018. - С. 330.
Положение об оплате труда работников ФГБОУ высшего образования КНИТУ-КАИ // Казанский национальный исследовательский технический университет им. А.Н. Туполева - КАИ: Официальный сайт. - 2018. URL: https://kai.ru/documents/10181/690854/Положение 0864-О об оплате труда (дата обращения: 01.04.2019).
Abramo G., Cicero T., D’Angelo C.A. What Is the Appropriate Length of the Publication Period over Which to Assess Research Performance? Scientometrics, 2012, vol. 93, no 3, pp. 1005-1017.
Abramo G., Cicero T., D’Angelo C.A. Assessing the varying level of impact measurement accuracy as a function of the citation window length, Journal of Informetrics, 2011, no 5, pp. 659-667.
Таблицы месячной и годовой инфляции в России // СтатБюро: Отдел департамента данных Официальный сайт. - 2018. URL: https://www.statbureau.org/ru/russia/inflation-tables (дата обращения: 01.04.2019).
Затраты на рабочую силу и заработная плата // Федеральная служба государственной статистики: Официальная статистика. - 2019. URL: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/wages/labour_costs (дата обращения: 01.04.2019).
Галеев И.Х. Анализ юзабилити системы Science Index // "Образовательные технологии и общество" - 2015. - V.18. - №4. - С.767-779.
Румянцев А.А., Хабибулин Р.Р., Александров А.С. Применение аппарата нечеткой логики при расчете рейтинга публикационной активности научных работников КНИТУ-КАИ // Прикладная математика и информатика: современные исследования в области естественных и технических наук: материалы V Международной научно-практической конференции (школы-семинара) молодых ученых. - Тольятти: Издатель Качалин Александр Васильевич, 2019. - С.278-281.

Еще

Статья научная