Модель процесса наведения авиационной противокорабельной ракеты в условиях перерыва поступления информации

Имеется класс систем управления, подверженных влиянию случайных возмущений и помех, управление которыми организуется на основе обработки некоторой информации, получаемой в процессе наведения. При наличии помех поток этой информации может прерываться, что делает дальнейшее управление невозможным. При перерывах в поступлении информации, необходимой для управления АПКР, система управления изменяет свою структуру, то есть происходит переход системы из управляемого состояния в неуправляемое. В связи с этим возникает задача оптимизации наведения, обеспечивающего функционирование объекта управления (т.е. АПКР) в условиях помех. Наиболее просто задача оптимизации в системах наведения с переменной структурой решается для линейных систем без ограничения на управление. Данная задача решена в [1; 2]. Однако определение оптимального наведения для динамических объектов управления, таких, как АПКР, описываемых системами дифференциальных уравнений высокого порядка, представляет достаточно сложную задачу. Кроме того, техническая реализация такого управления трудноосуществима. Поэтому для создания оптимального наведения АПКР необходимо идти по пути упрощений исходной системы дифференциальных уравнений, описывающих функционирование динамического объекта, позволяющих снизить ее порядок. Далее, определить уравнения оптимального линейного фильтра и оптимального регулятора [l], чтобы в дальнейшем включить их в исходную систему.

1. Постановка задачи

Пусть объект управления описывается системой дифференциальных уравнений, приведенной к нормальной форме Коши, линеаризованных методом Тейлора относительно опорной траектории [3].

^п = - v e ,

. А *

e = A a +— W n ,

v

ВЕСТНИК 2017

a = - c a - 5 , a a

• ■5 , = K u ( Tu + u ) - ( Kv— + K Г A ) a - K _r a - K r —-W „ ,

^u = -- ^u + ^{c (}A + ^ ,), ^A = _Ф цв - _Ф р

To

^Ф цв = D ^(ф цв - ^{e ) ; Ф} p = ^u ,

W ₌ —Кил ₊ л

" n     J ” n ⁺ ^ W ,

.

где n(t) - линейное отклонение АПКР от опорной траектории, 0(t) - вариация угла наклона траектории, a(t) - угол атаки, 5b(t) - угол от клонения руля, u (t) - сигнал управления, А(t) -параметр управления, фцв (t) - угол визирования цели, Фр (t) - угол отклонения координатора цели, Wn(t) - случайная составляющая скорости ветра, v(t) - скорость АПКР, D(t)- дальность до цели; Ки, Ти, Ка, КГ, К0, Т0 - коэффициенты системы управления, Т^ - постоянная времени формирующего фильтра; ^ , ^W - нормальные белые гауссовы шумы, характеризующие ошибки системы управления и турбулентность атмосферы, с интенсивностями G^ и GW, соответственно; А, А',са, с5, са - аэродинамические коэффициенты, значения которых приведены в [3], с - коэффициент, принимающий значения с = 1 при отсутствии перерывов в получении необходимой для управления информации и с = 0 при наличии таких перерывов. Структурная схема системы (1) изображена на рис. 1.

Требуется определить оптимальное управление АПКР, на основании наблюдения фазовых координат, минимизирующее определенный критерий качества.

При наличии наблюдений вектора Z( t ) [2] наилучшей оценкой функционала ^tk

10(t0,Y,u,Tk) = l1(Y,tk) + J/2(Y,u, )dT, в смысле минимума среднего квадрата ошибки оценки, является условный риск (условный критерий)

I» = M[Iо(10, Y,и,tk )|z(т),10 < Т < tk ] = Mz[I„1, который для данной задачи примем в следующем виде [2]:

Z*

1 0 = M z

(< 9 цв ⁽ t k ) ) ^{2 +} K ¹ j[ ( ^{U (} t ) ) ^{2 dt +} K ² If ( ф цв ⁽ t ) ) ^{2 dt} t_{k 0} t_{k 0}

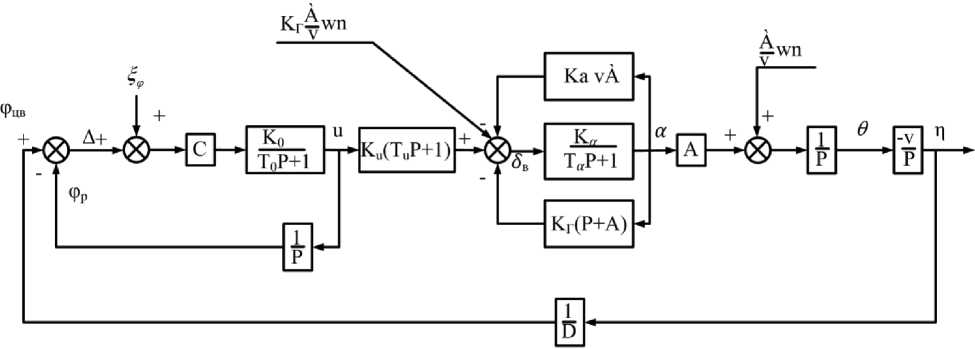
Рис. 1. Структурная схема системы наведения АПКР

где M z - операция условного математического ожидания, t_k - конечный момент управления, U - искомое управление, К 1 , К 2 - заданные постоянные коэффициенты.

• 2.    Решение

Как было уже сказано, определение оптимального управления для объекта, описываемого системой (1) высокого порядка n = 7, является сложной задачей. Кроме того, наблюдаемыми фазовыми координатами, которые могут быть измерены имеющимися устройствами, являются угловая скорость линии визирования цели ® = ® цв = Ф цв и нормальное ускорение объекта a n = у 0 . Для получения упрощенной математической модели функционирования системы управления, включающей в себя дифференциальные уравнения относительно го и a n , используем систему (1), приняв следующие допущения:

• -    координатор цели заменим эквивалентным апериодическим звеном, входом которого является угловая скорость линии визирования цели го с аддитивной помехой N _m , представляющей собой приведенный к угловой скорости шум ^ ,;

• -    постоянную времени T u форсирующего звена системы управления примем равной постоянной времени эквивалентного апериодического звена координатора цели Т э ;

• -    будем считать, что постоянная времени формирующего фильтра Т ф равна постоянной времени апериодического звена, описывающего динамику объекта управления (АПКР);

  - скорость АПКР будем считать постоянной.

Умножив обе части второго уравнения системы (1) и продифференцировав второе и шестое уравнения этой системы с учетом принятых допущений и остальных уравнений системы (1), получим уравнения, описывающие функционирование системы управления АПКР в следующем виде:

an = Т^(vU - an + ^a ) ,

T

а

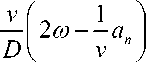
а уравнения измерителей в виде:

' Z. = c (а + N. ),

". Z.. = an + N.                         (4)

T.

а

T

а

В (3) величины U и основании выражений: c

U = AKK Z„ К• = — u а а а

, c * а определяются на

c .*

_ а c . ’ а

q ( t о ) =

Р о ^ У о v 0 ^Q a

c _a *    ^C a   ^C 8 ^KГ ,

C . а

=^{- (} c

- cK vA о a

- c « K Г A ) ,

где T* и К _а * - постоянная времени и коэффициент усиления апериодического звена, учитывающего инерционность объекта, ^ . - приведенный к нормальному ускорению белый шум, характеризующий турбулентность атмосферы с интенсивностью G a = ( АТ Ф )² G W ^; N „ и N _a - белые шумы, характеризующие ошибки измерителей с интенсивностями Q_m и О , соответственно.

^а s^ a

Структурная схема упрощенной математической модели, описывающая функционирование объекта, системы управления, приведена на рис. 2.

Задача определения оптимального управления для системы, описываемой уравнениями (3) и (4), решена в [2].

Решением этой задачи являются уравнения оптимального регулятора:

U = r

. T. . а —а а

Dn

V

где

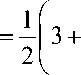
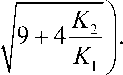
И уравнения оптимального фильтра:

ВЕСТНИК 2о17

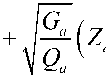
,       1

а„ = —

vU

n T . а

: V _      . .    1 _

У = — [(2 - cq)а - Z„

Dv^{a n}

,

⁺ cqZ a ^],

где q=D(3q - cq2).

Из (6) следует, что оптимальный фильтр имеет две структуры, определяемые коэффициентом с , принимающим значение c = 1 при отсутствии перерывов в получении информации о цели управления и c = 0 при наличии таких перерывов (когда коммутатор замкнут или разомкнут ).

Переключение структуры фильтра через ключ c обеспечивает перевод работы фильтра из режима фильтрации в режим памяти.

Для решения уравнений фильтра необходимо задать соответствующие началь- ные условия, которые ниями [2]: <2. (tо ) = ma, определим выраже-( t0 ) , O) ( tо ) = mm ( tо ) ,

ВЕСТНИК 2017

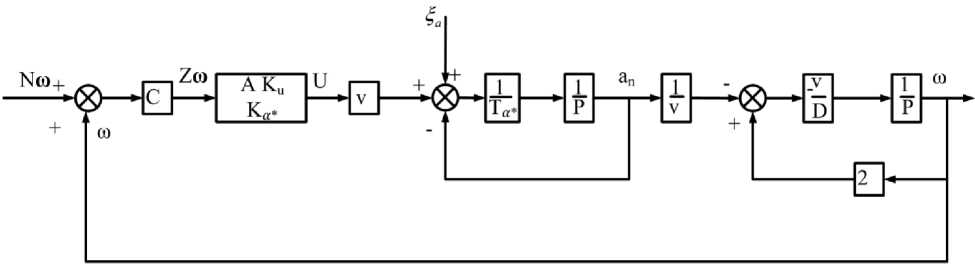
Рис. 2. Упрощенная структурная схема координатора цели системы наведения ракеты

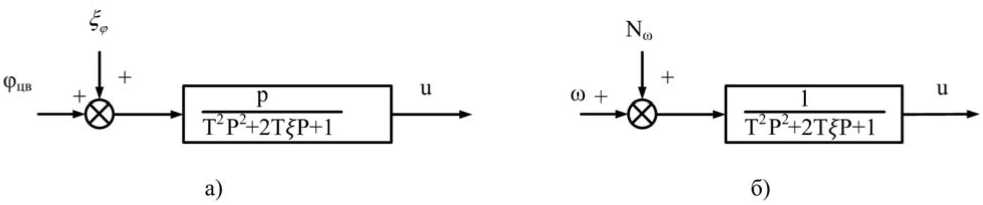
Рис. 3. Преобразованная структурная схема координатора цели

Кроме того, для решения уравнений фильтра (6) необходимо определить интенсивность Q ® белого шума N ® , представляющего собой приведенный к угловой скорости шум ^ _ф c интенсивностью G _ф , для чего проведем эквивалентное структурное преобразование координатора цели, изображенного на рис. 2. Преобразованная структурная схема координатора цели представлена на рис. 3.

Определим установившуюся дисперсию выходного сигнала D_u системы (рис. 3а) при воздействии на нее входного сигнала в виде белого шума ^_ф с заданной интенсивностью G _ф [4].

где Ф 2 ( p ) =

T2 p2 + 2T^p +1

.

Из условия равенства дисперсий, определяемых по формулам (7) и (8), получим выражение для определения интенсивности:

I Ф (i®)l2 d®

го

u

где

G

-го

^Ф 1 ( ^P ) =

^=т-4

-^--------; T = 0-

T2 р2 + 2т^р +1     K^ о

— . ^ - коэффициент демпфирова-

ния.

Аналогичным образом определим дисперсию выходного сигнала системы (рис. 3б) при воздействии на нее белого шума N ® с интенсивностью Q ® : .

-го

I Ф2 (i®)l2 d®

ф

Для вычисления интегралов в (9) применим формулы интегралов от дробно-рациональных функций [4]:

СО

-го

СО

-го

п 2T3§ ’

п 2т^

.

Подставив (10) в (9), получим окончательное выражение для определения Q ® :

Q ® T 2 ^Gф .

В результате получен алгоритм оптимального управления, описываемый уравнениями (5) и (6), структурная схема которого представлена на рис. 4.

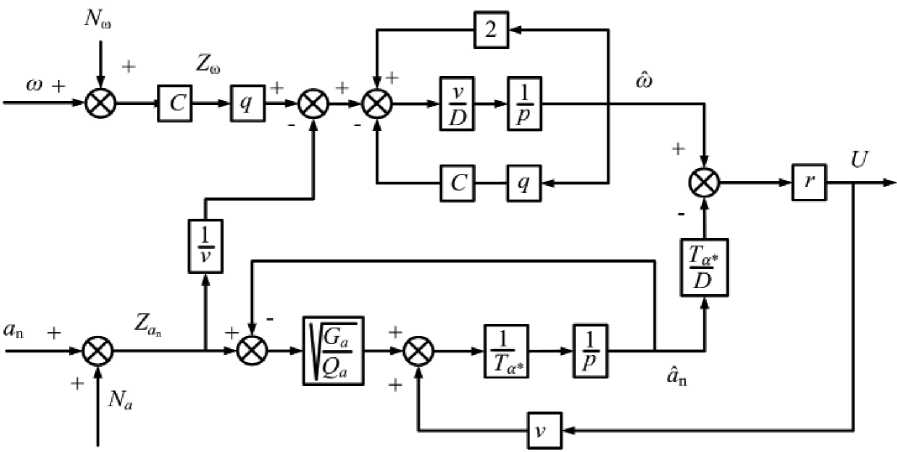
Рис. 4. Структурная схема оптимального фильтра и оптимального регулятора системы наведения

Включив полученное уравнение оптимального управления (5), (6) в исходную систему (1), получим математическую модель процесса функционирования системы управления, имею-

П = - v9,

■            A'

9 = Aa +—Wn,

v a=-— a - —s,, ca     ca t.

s = K„o a-—fr - KvA + KrA\a -ь        u 0                   n i у a              г j щую случайную структуру с двумя возможными состояниями при наличии в законе управления оптимального регулятора и оптимального фильтра:

A = Рцв - Pp ,

W n =- X" W n + ^ W

Tф iq = — (3q - cq2], r =1 3 + /9 + 4K2- .

D ’    2 ^ ^    K1 J

ВЕСТНИК 2017

- K Г a - K Г —Wn, v к v                 1

® =   [(2 ^- cq) ю ^- Z a n + cqZ J,

1 al n

vU + GMz - (I )

_Qa    a n     n

Z ® = T u i l + u ; Z a n = a _n + N a ; a _n = v 9,

U = r

L t. „ to ——a

I D

\

K

u 0

r

AK

a

u1=- 7- u+cK0 (л+^p M1 - c)® To        To

Ha рис. 5 изображена структурная схема системы наведения АПКР, описываемой системой (11) при наличии оптимального управления.

Вывод

Таким образом, подача оценки ω через ключ (1 – c ) обеспечивает разворот координатора в некоторую прогнозируемую точку в случае перерыва в поступлении информации о цели управления. В разработанном законе наведения ракеты переход от одного состояния в другое обеспечивается ключом с , который управляется обнаружителем-анализатором мерцающей помехи.

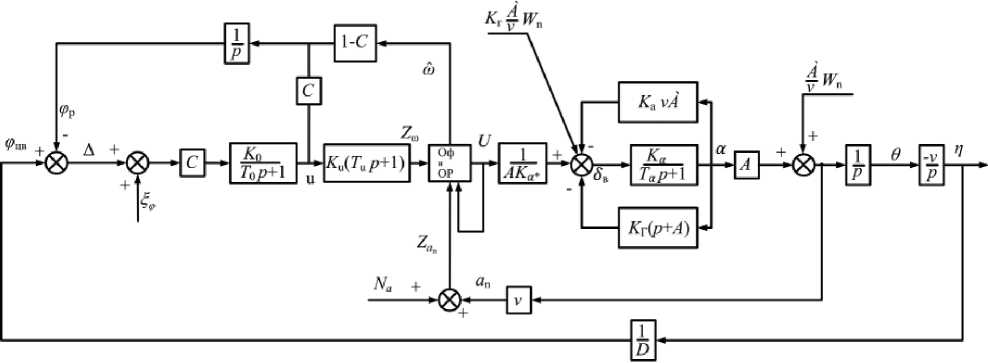
Рис. 5. Структурная схема системы наведения АПКР с использованием оптимального управления

ВЕСТНИК 2017