Модель процесса с кусочно-постоянными экстремалями для минимизации потерь витаминов при сушке бахчевых культур

К бахчевым культурам относят плоды арбузов, дынь, кабачков и тыквы. По данным ФГБУН «ФИЦ питания и биотехнологии», рекомендуемая норма потребления бахчевых плодов составляет 30 кг на человека в год. Наиболее характерным представителем семейства тыквенных культур – Cucurbitaceae считается дыня, на которую приходится примерно 25% от потребления всех бахчевых культур.

Однако распределение ее потребления в свежем виде значительно отличается по зонам страны – от 60 кг в регионах устойчивого земледелия, до 1 кг в отдаленных северных районах. Мякоть дыни содержит 10–15% сахаров, крахмал, витамин С (20 мг/100 г), каротин и фолиевую кислоту. Плоды имеющие оранжевую мякоть, содержат более 1 мг% β-каротина [3]. Для продления сроков хранения дыни ее сушат ломтиками, в виде порошка или изготавливают варенье и джемы. Традиционные способы обезвоживания и продления сроков хранения плодов бахчевых культур и амаранта, приведены в источниках литературы [3–5]. В работе Е.В. Иночкиной описаны принципы совершенствования конвективной СВЧ и вакуум-осциллирующей сушки растительного сырья [1, 2]. Важное значение уделяется решению задач нелинейной оптимизации процессов теплопереноса при минимизации кусочно-линейного функционала [6]. В работах профессора С.В. Усатикова впервые вводится понятие «интеграла памяти» для моделирования процесса хранения растительного сырья [7, 8]. В работе Л.С. Петровой с помощью методов математического моделирования процессов тепловой обработки кусочно-однородных тел, учитывалась релаксация теплового потока [9].

Например, в работе [10] идентифицированы кусочно-линейные и кусочно-нелинейные процессы. Мощный алгоритм управления системой получен с помощью системы линейных дифференциальных уравнений.

Сушка сырья микроволновым излучением обладает высокой скоростью и повышенной эффективностью [11–14]. Суть «импульсных» технологий состоит в проведении технологии сушки циклически. Предложено использовать вакуумный импульсный способ сушки сырья за счет СВЧ-нагрева и с периодическим резким обдувом высушиваемого продукта инертным газом [1]. В [2] сформулированы выводы по режимам сушки, установлена зависимость давления в аппарате (при снижении влагосодержания ниже предела гигроскопичности) от температуры высушиваемого материала. Предложен способ регулировать процесс обезвоживания бахчевого сырья по его дифференциальной усадке. Лучшие результаты по качеству сухих продуктов достигаются при длительности СВЧ-обработки в течение 2 мин и подачи импульса инертного газа в течение 20 с. Предложенная технология вакуумной импульсной сушки сырья с циклическим подводом тепла, позволяет получать сухую продукцию более высокого качества по сравнению с продукцией вакуумно-кондуктивной сушки [2].

Материалы и методы исследования

Основным объектом исследований выбрана дыня раннеспелого сорта Таманская, прошедшая Госсортоиспытание в Краснодарском крае (автор Н.И. Цибулевский). Для экспериментов использовали плоды дыни округлой формы массой 1,3–1,5 кг, с белой сладкой мякотью, с содержанием сухих веществ 13%, витамина С 30 мг%, с суммой легкоусвояемых углеводов 17,5% и суммой сахаров 10,6%.

Предложен новый СО 2 -сверхкритический способ сушки, физическая сущность которого заключается в повышении растворимости паров воды в сверхкритическом СО 2 . Досушивали сырьё обработкой в электромагнитном поле частотой 2400–3000 МГц и длине волны от 12 до 10 см.

При выполнении работы были использованы современные стандартные методики исследований химических, биохимических, микробиологических, органолептических исследований. Массовую долю сахаров определяли по ГОСТ 8756.13.87, сухих веществ по ГОСТ 28561-90, содержание витаминов и микроэлементов – по прописям Госфармакопеи.

Результаты исследований

Для оптимизации процесса обезвоживания бахчевого сырья с использованием экспериментальных данных получить регрессионные модели зависимости влажности W и содержания витамина Сот температуры T и давления P в зависимости от времени t. Применение метода регрессионного анализа, как наиболее распространенного способа, связано с выбором многомерного анализа с максимальным индексом корреляции R, с возможно меньшим числом параметров и уровнях значимости α. Однако такой подход не позволяет описывать и строить модели протекания биохимических и физических процессов в сырье, а может только количественно связывать получаемые в эксперименте величины. В связи с этим упомянутые регрессионные зависимости нельзя применять за пределами экспериментальных данных из-за низкой прогнозной ценности. Далее, полученные регрессионные зависимости не имеют памяти и не учитывают влияние предыстории процесса на сегодняшнее состояние: в частности, деструкция витамина С необратима, несмотря на то, что регрессии выдают показатели «мгновенно и обратимо реагирующими» на изменение факторов. В [5, 6] показаны возможности использования известных интегралов памяти (нелокальных по времени, с различной наследственностью, релаксационным ядром и др.) для вывода зависимости состояния сырья от динамики процесса.

В данной работе, на основе полученных в экспериментальных данных двухэтапного процесса сушки дыни сорта Таманская, предложены регрессионные модели с релаксационным ядром [5, 6] для зависимости влажности W и содержания витамина С от переменных по времени t температуры T и давления P . На рисунке 1 представлена кинетика двухстадийной сушки ломтиков дыни.

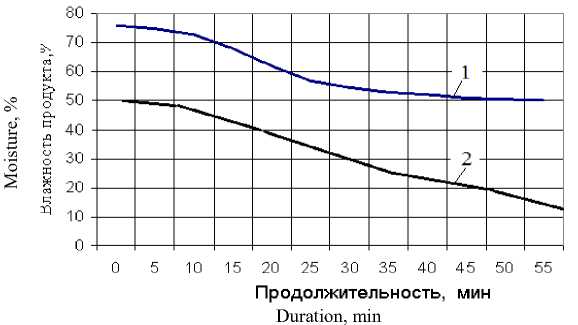
Рисунок 1. Кинетика двухстадийной сушки ломтиков дыни СО 2 -сушка, 2 – СВЧ-досушка

Figure 1. Kinetics of two-stage dryng of melon slices 1 – СО 2 -drying, 2 – microwave drying

Авторами поставлена задача оптимального управления процессом сушки для поиска термобарического режима T ( t ) и P ( t ), максимизирующего содержание витамина С в конце сушки, при заданных условиях на влажность. Получено решение задачи для случая кусочно-постоянных T ( t ) и P ( t ) на отдельных N шагах каждого из 2-x этапов.

Разработаны нелокальные по времени регрессионные модели (с релаксационным ядром) процесса сушки бахчевых культур.

В таблице 1 приведены данные о двухэтапном процессе ломтиков дыни.

Таблица 1.

Экспериментальные данные о двухэтапном процессе сушки дыни сорта Таманская

Table 1.

Experimental data on a two-stage process for drying a melon of Tamanskaya variety

1 этап сушки с использованием диоксида углерода в сверхкритическом состоянии 1 drying step using carbon dioxide in the supercritical state	№ шага опыта Step no. of experience	Условия опытов | Experimental conditions			Результаты измерений Measurement results
		Температура, °C Temperature, °C	Давление, МПа Pressure, МРа	Влагосодержа-ние начальн., % Moisture content Initial, %	Витамин С мг/100 г. Vitamin C мg/100 g	Влагосодержание конечн., % Moisture content Finite, %
	1	33	32	90	22	74,5
	2	36	34	74,5	21,56	67,5
	3	38	36	67,5	21,10	52
	4	42	38	52	20,76	45,5
	5	44	40	45,5	20,43	41
2 этап сушки СВЧ + вакуум 2 stage of microwave drying + vacuum	1	35	0,007	41	20,58	35,5
	2	36	0,007	35,5	20,65	28,5
	3	37	0,008	28,5	20,77	20
	4	38	0,008	20	20,83	14,5
	5	38	0,008	14,5	20,88	12

Продолжительность каждого i -го ( i = 1…, N ; N = 5) шага опыта j = 1 этапа – 30 мин, продолжительность каждого шага опыта j = 2 этапа – 2 мин

The duration of each i -th ( i = 1…, N ; N = 5) of the experiment step j = 1 stage is 30 minutes, the duration of each experiment step is j = 2 stages – 2 min

Далее целью является построение модели прогноза величин показателей качества продукта с течением времени, если известны их величины в некоторый начальный момент времени. Общий вид регрессионной модели с интегралом памяти (типа Вольтерра, 2 рода), учитывающий предысторию процесса, для некоторого показателя R следующий:

Обработка по (3) данных таблицы 1 в МаthСАD позволила получить следующую связь между термобарическим режимом и показателями сырья (рисунок 2) :

t . < ^a 1 ^jT ^{+ a} 2^j T ² + ^b i ^{P +}^ - a,₍t - ,     (4)

e ⁽ ) d , , v⁷) ^j k+ b ₂ ^jP ² + cTP     J

R ( t ) = f ( t , W ( t ), T ( t ) ) + j ^ ( t - t , W ( t ), T ( t ), R ( t ) ) d , , ⁽¹⁾ 0

где вид функций f и K (ядро типа свёртки) должен быть задан. Если ядро K линейно по W, T с множителем P , а также линейно либо показательно (т. е. с «кратковременной памятью») по времени, то (1) как частный случай интегрального уравнения с вырожденным ядром эквивалентно некоторому релаксационному дифференциальному уравнению, с решением в виде , либо затухающих колебаний, либо монотонно устанавливающимся. Явные регрессионные модели с памятью получаются при ядре K , не зависящем от искомого показателя R . Далее ниже рассмотрены f, квадратичное по W и T , а также K , показательное (т. е. с «кратковременной памятью») по времени:

C ( t ) = C 0 ^j +

	f a i A a 2		f - 3.399 x 10 - 3 A 0.015
где	b 1 b 2 c к a J	=	0.022 0.017 - 0.032 к 0.143 v	при j = 1

	f a 1 A		f - 0.027 A
	a 2		8.742 x 10 - 4
и	b 1		0.022	при j = 2
	b 2	=	0.017
	c		- 0.027
	a		0.474

a1-мг/100г/сек/град; a2-мг/100г/сек/град/град;

b1-мг/100г/сек/МПа; b2-г/100г/сек/МПа/МПа;

c-мг/100г/сек/МПа/град; alfa- 1/сек .

R ( t ) = R (0) +

t. a 1 T ( t ) + b 1 W ( t ) + a 2 ( T ( t ) ) 2 ⁰ . ' b 2 ( ^P ( ^T ) ) 2 ⁺ c ^T ( ^T ) ^P ( ^T )

+

e ^{a ( T -} t ) d T , ⁽²⁾

где параметры регрессии а 1' , а 2' , b 1' , b 2' , С и d

определяются для каждого j -го этапа методом наименьших квадратов по N шагам-измерениям с интервалом ∆ t^j по времени показателя R i ^j в зависимости от влажности W i^j и температуры зерна Т (1 < i, 1<j<2). После сплайн-интерпо-ляции функций W^j(t) и Т^j(t) по измерениям Wi^j и Тi^j минимизируется функция ошибки:

t -f A^jT + A^jT ² + b,^jp +)  „ j,, .

W^j ( t ) = W_o^j +      ¹ . A ^{2         1}        e ^{- e (} t ^-T ) d T ,

⁰   0 k+ B 2 ^j p ² + C^jTP     J

f a1 A a2 f-1.152 x 10-3 A 6.534 x10-5 где b1 b 2 c кa J = -0.015 -5.308 x10-3 5.188 x 10-3 к-6.887 x 10-3; при j = 1 fai A f 2.655 A

E ( a i , a 2 , b ,, b 2 , c ,a ) =

N

=Е i=1

R i

к

i -Д t

^{R 0 + j}

^a i ^T ( ^T ) ^{+ b} 1 ^W ( ^T ) ^{+ a} 2 ( ^T ( ^T ) ) 2 ' ^b 2 ⁽ P ^{(T ) ) 2 +} c^{T (T} ) ^{P (T} )

) , .. ->„,

J

J

Заметим, что стандартные пакеты матема-

a2 -0.092 и b1 = 0.396 при j = 2. b 2 -1.420 x10-3 c 64.868 к a к 0.396

тической статистики не производят обработку

A1-%/сек/град; A2-%/сек/град/град; B1-%/сек/МПа; B2-%/сек/МПа/МПа; C-%/сек/МПа/град; beta-1/сек

моделей (1) или (2), необходимо применение средств пакетов МаthСАD, Maple, MatLab,

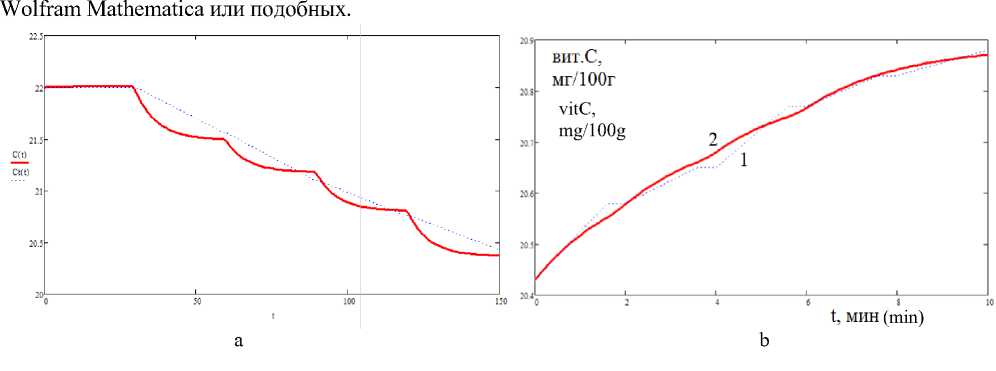
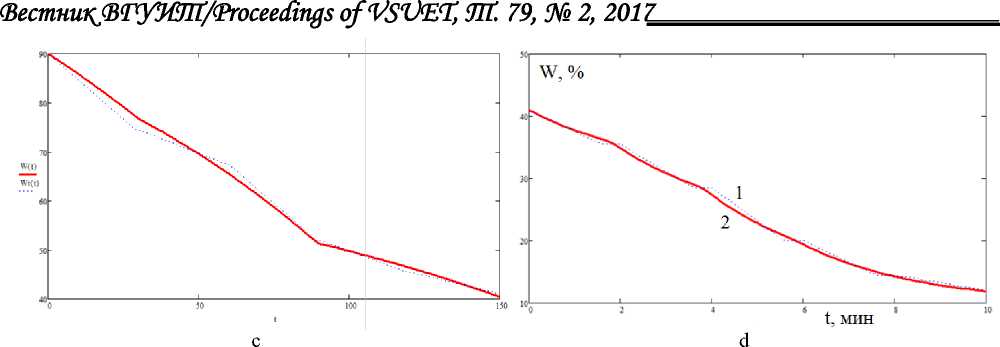
Рисунок 2. Регрессионная модель для содержания витамина С (a – j = 1, b – j = 2) и влажности (c – j = 1, d – j = 2): 1 – данные табл. 1, 2 – соотношения (4) и (5)

Figure 2. Regression model for the content of vitamin C (a– j = 1, b– j = 2) and humidity (c – j = 1, d – j = 2) : 1 – data of tables 1, 2 – relations (4) and (5)

Задача оптимизации с целью снижения потерь витаминов при сушке бахчевых культур

Соотношения (4) и (5) устанавливают связь между термобарическим режимом и показателями сырья для каждого этапа. Это позволяет поставить задачу оптимального управления процессом сушки для поиска термобарического режима T ( t ) и P ( t ), максимизирующего содержание С в конце каждого j -го этапа сушки – в моменты времени t к^j , при заданных условиях W к^j на влажность:

, j k ( a1 ’T + a 2 ’T 2 + b1 jP + ^ -J tk1 -T) vitCj = Coj + I                     Ie '   'dr ^ max k 0 о 1+ b21P 2 + CTP      J при T (t )> 0; Pj (t )> 0; Wj (tkj ) = Wkj, где

W^j ( T 1 ^j , ^ , T n ¹ , P1', ^ , P _n' ) =

N

= W^j +— У

⁰ в t!

<

A 1^j T i^j + A ₂ ^J ( T^J ) 2 + B 1 Pi + B ₂ ^j ( P^j ) 2 + C N P

A

_e - e ^{j 30} ( ^N - i ) ( 1 _ e - 30 e ^j ) .

J

Задача математического программирования (7)–(8), как задача на условный экстремум функции при смешанных ограничениях (при одном ограничении типа равенства и двух типа неравенств – требовании неотрицательности аргументов T и P ), может быть решена методом множителей Лагранжа λ. Функция Лагранжа имеет вид, N = { 2 ₀ ^j , Д ’ , X ^ , X ^ }:

t k^j

W ^j ( t k^ = W o ^j + J

( A / T + AJ ² + J +) - ’_t- -t )

Ie tt v+B2j P2 + CJ TP     J

P ( T /, _ , T n ¹ , P-, _ , PN, N ) =

WK = W^j ( tk^J ) = Wo^j

^t k

+ J

( A/T + A J ² + B/P +) - в ( t^ -t ) , I e ^v t t

(+ B ₂ ^j P ² + C^jTP      J

= X 0 vitC l + NW / - X 2 ^j T - X 3¹ P

Необходимое условие экстремума первого порядка приводит к алгебраической системе уравнений с 2 N + 1 неизвестными:

В технологических процессах сушки обычно в пределах каждого шага каждого этапа T ( t ) и P ( t ) поддерживаются постоянными: равными Т 1^j …, Т N^j ; Р 1^j …, Р N^j . Тогда задача (6) примет вид:

vit C ( T ,..., T N , P ..... P N ) ^ max    (7)

при w ¹ ( / ,..., TN, p / , ^ , p n ) = W k ¹

и т/ > 0,..., TN > o, P^j > 0,..., P N > 0 ,

где

^{vit C}K = ^C o ^j

- a jnN N

+ aj t!

.-<

N

(

= c¹ +— у ⁰    a ^j t !

(

a1’ T i’ + a.

a1’ Ti’ + a.

( T ) 2 + b ' P

+ b 2 ( P ) 2

( T ) 2 + b P

\

e " tl _ =

+ b 2 ^j ( P ) 2

e

- a ^j

30 ( N - i ) (.

1 - e

,-30 a ^j

) .

-a-3o-(N-i)         -30aj x e           • (1 - e )

a ^j

a j + 2 a 2 ( T/' ) + c^j P/ +

- e - 30 - ( N - i )          - 30 e

+ X 1 ^j-------- e (-------) A ’ + 2 A 2 (T^J) + CP =0 (10)

- „ a’ -⁰- ( ^N - 1 ) ,M _ - ³⁰ ’.

e--------(—e----) bj + b2j( P’) + PT/ + aj

- в - 30 - ( N - i )          - 30 в

+N e --------'^ ^e —) b; + b 2 ( p/ ) + ct/ = 0

где i = 1…, N – указывает № шага каждого -го ( = 1; 2) этапа.

При N = 5 алгебраическая система (10) имеет 11 уравнений с 11 неизвестными:

-^{30 a} )                          e

—- ( a i + 2 a 2 T + cP i ) + —

, -3

- ^{T - 304}(i — e —

— a - 30 - 4

e (i — e

a

— a - 30-3         — 30 a \ e      (i — e )(

a

— a - 30-2         — 30 a \ e     (i — e )

a

— a - 30-i          — 30 a \ e ( 1 — e )(

a

— a - 30-0         — 30 a \ e     (i — e )

a

— a - 30-4         — 30 a \ e     (i — e )

a

— a - 30-3         — 30 a \ e      (i — e )(

a

— a - 30-2         — 30 a \ e     (i — e )

a

— a - 30 - i          — 30 a \ e (i — e )(

a

— a - 30-0         — 30 a \ e     (i — e )

e

( a i + 2 a 2 T 2 + cP 2 ) +—

, —

e

( a i + 2 a 2 T 3 + CP 3 ) +—

в

• - ^{T - 30 3} (i — e

T"

• -^{в - 30 - 2} (i — e

30 в

—) ( A i + 2 A 2 T + CP i ) - X = 0

30 в

—) ( A i + 2 A 2 T 2 + CP 2 ) - X = 0

— 3

— 3

e

( a i + 2 a 2 T₄ + cP₄) +—

в

- ^{e - 30i}(i — e —

30 в

—) ( A i + 2 A 2 T 3 + CP 3 ) - X = 0

e

( a i + 2 a 2 T 5 + CP 5 ) + —

30 в

—) ( A _i + 2 A ₂ T ₄ + CP ₄) - X = 0

в

• - ^{e - 30 - 0}(i — e

T"

• -^{в - 30 - 4} (i — e "

-

— 3

e

( a i + 2 a 2 P i + cT i ) + —

e

( a i + 2 a 2 P 2 + cT 2 ) +—

e

( a i + 2 a 2 P 3 + cT 3 ) +—

—

e

( a i + 2 a 2 P₄ + cT₄^ +—

( a _i + 2 a ₂ P 5 + cT ₅) I a

Для случая кусочно-постоянных T ( t ) и P ( t ) на отдельных N шагах каждого из 2-x этапов, получено средствами МаthСАD v. 15 решение системы (10): рисунок 2 и 3 для 1 этапа, рисунок 4 – для 2 этапа.

30 в

—) ( A i + 2 A 2 T 5 + CP 5 ) - X = 0

— 3

в

• -    ^{e - 303}(i — e

T

• -    ^{T - 302}(i — e

- 30 в х

—) ( A + 2 A 2 P i + CT i ) - X = 0

30 в

—) ( A i + 2 A 2 P 2 + CT 2 ) - X = 0

— 3

— 3

в

- ^{T 30i}(i — e

— В - 30 - 0 e

+-----

a

30 в

—) ( A i + 2 A 2 P , + CT 3 ) - X = 0

— 3

в

(i — e

T

- 30 в х

—) ( A _i + 2 A ₂ P ₄ + CT ₄) - X = 0

,—30 в x

----) ( A i + 2 A 2 P 5 + CT 5 ) - X = 0

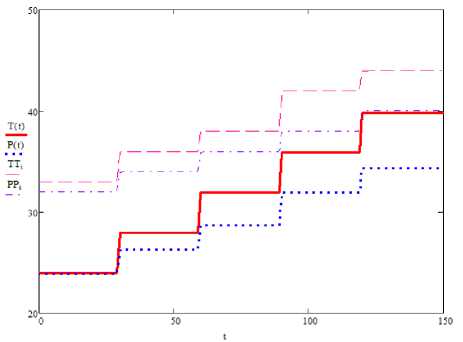
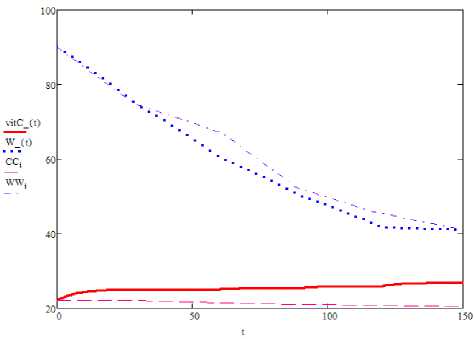
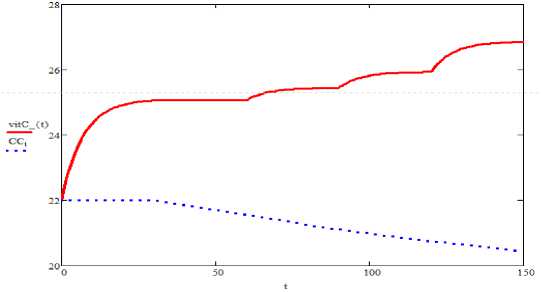
На 1 этапе решение (10) существует и единственно, доставляет максимум vi tC, увеличивая конечное содержание С на 22,7% (с 22 % до 27%) за счёт оптимального снижения температуры и давления. Термобарические экстремали 1 этапа показаны на рисунке 4a .

b

c

Рисунок 3. Оптимальный режим 1-го этапа: a – термобарические экстремали; b – динамика влажности; c – динамика содержания витамина С

Figure 3. Optimum mode of the 1st stage: a – thermobaric extremals; b – dynamics of humidity; c – dynamics of vitamin C content

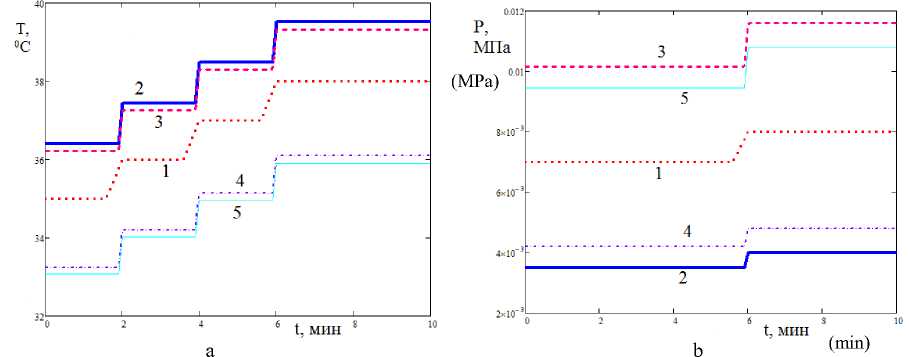
Рисунок 4. Варьирование температуры T и давления P на 2 этапе: 1 – заданные T и P в эксперименте, 2 – повышение T на 4% и понижение P на 50%; 3 – повышение T на 3% и повышение P на 45%; 4 – понижение T на 5% и понижение P на 40%; 5 – понижение T на 6% и повышение P на 35%

Figure 4. Variation of temperature T and pressure P in stage 2: 1 – given T and P in the experiment, 2 – increase of T by 4% and decrease of P by 50%; 3 – increase of T by 3% and increase of P by 45%; 4 – decrease in T by 5% and decrease in P by 40%; 5 – decrease in T by 6% and increase in P by 35%.

(min)

a

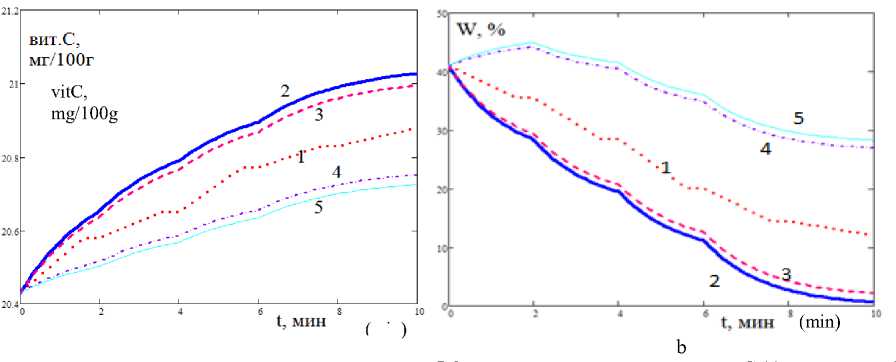
Рисунок 5. Влияние варьирования температуры T и давления P 2-го этапа на содержание витамина C (а) и влажность W (б): 1 – при заданных T и P в эксперименте, 2 – при повышении T на 4% и понижении P на 50%; 3 – при повышении T на 3% и повышении P на 45%; 4 – при понижении T на 5% и понижении P на 40%; 5 – при понижении T на 6% и повышении P на 35% Figure 5. Influence of temperature variation T and pressure P of the 2nd stage on the content of vitamin C (a) and humidity W (b): 1 – for given T and P in the experiment, 2 – for T increase by 4% and P decrease for 50%; 3 – with an increase of T by 3% and an increase of P by 45%; 4 – with a decrease in T by 5% and a decrease in P by 40%; 5 – with a decrease in T by 6% and an increase in P by 35%

На 2 этапе решения (10), доставляющего максимум vitС, не существует. Это означает, что при заданной конечной влажности W к оптимальными для 2-го этапа следует признать те T ( t ) и P ( t ), которые обеспечивают W к , т. е. если заданная начальная влажность W 0 равна экспериментальной, то реализованный в эксперименте термобарический режим будет оптимальным. Это показано на рисунках 4, 5. Повышение температуры приводит к повышению содержания витамина C вследствие уменьшения влажности, но кроме пересушивания, возникает нежелательное разрушение витамина C. Уменьшение давления тоже приводит к уменьшению влажности и повышению содержания витамина C, причём без нежелательного его разрушения, но влияние давления намного (на порядок)

меньше влияния температуры и существенное снижение давления может оказаться неприемлемо технически и материально затратным.

Выводы

• 1.    Предложена нелокальная по времени регрессионная модель прогноза динамики содержания витамина С и влажности в процессе двухэтапного процесса сушки дыни сорта Таманская, позволяющая учесть предысторию процесса и его влияние на текущее состояние сырья. Применение модели с «кратковременной памятью» даёт возможность корректировать такие ограничения традиционно применяемого регрессионного анализа, которым в литературе не уделяется достаточного внимания: предложение только количественных связей, наблюдаемых

• 2.    Модели с «кратковременной памятью» устанавливают связь между термобарическим режимом и показателями сырья для каждого этапа. Это позволяет поставить задачу оптимального управления процессом сушки для поиска термобарического режима T ( t ) и P ( t ), максимизирующего содержание витамина С в конце каждого j -го этапа сушки, при заданных условиях на влажность. В технологических процессах сушки обычно в пределах каждого шага каждого этапа T ( t ) и P ( t ) поддерживаются постоянными. Тогда задача сводится к математическому программированию, решение которой может быть получено методом множителей Лагранжа.

• 3.    Задача математического программирования решена средствами МаthСАD. На 1 этапе решение существует и единственно, доставляет максимум содержания витамина C, увеличивая

в эксперименте величин вместо описания и построения моделей биохимической и физической сути процессов, а также отсутствие учёта влияния предыстории процесса на его текущее состояние.