Модель процессов формирования и распространения инфракрасного излучения теплоизлучающего аэрозольного образования

Цитирование: Козирацкий, Ю. Л. Модель процессов формирования и распространения инфракрасного излучения теплоизлучающего аэрозольного образования / Ю. Л. Козирацкий, Д. В. Прохоров, В. А. Баев // Журн. Сиб. федер. унта. Техника и технологии, 2021, 14(7). С. 812–819. DOI: 10.17516/1999-494X-0350

образования, попадающие на данную частицу и рассеиваемые в направлении фотоприемника. Рассмотрим процессы формирования и распространения ИК-излучения такими частицами. Геометрия задачи представлена на рис. 2.

Рассмотрим в элементарном срезе dz элементарный объем dV (рис. 2), в котором в некоторый момент времени t находится определенное число частиц с определенной температурой. При этом

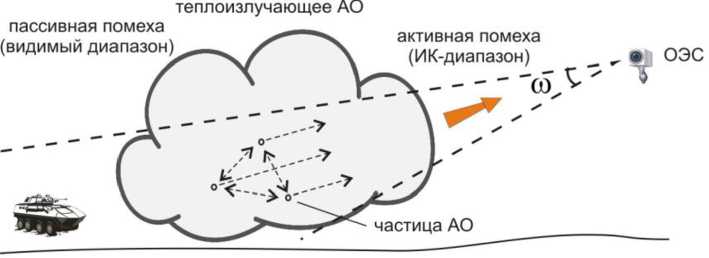
Рис. 1. К постановке задачи

Fig. 1. To the problem statement

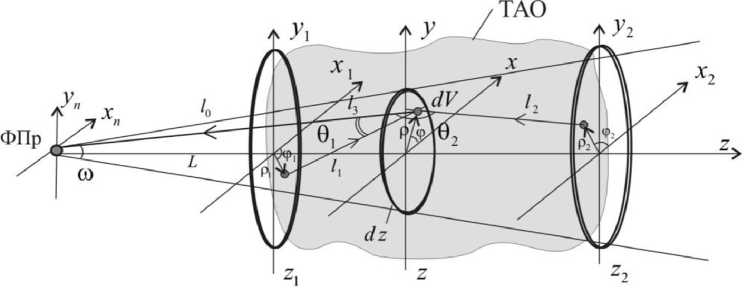
Рис. 2. Геометрия задачи

Fig. 2. Geometry of the problem будем предполагать, что температура частиц в элементарном объеме одинакова. Тогда частицы элементарного объема dV будут излучать и переизлучать электромагнитный поток, величина которого на длине волны λ будет характеризоваться спектральными коэффициентом излучения ελ, показателем поглощения knλ и показателем рассеяния σλ этого объема.

На рассматриваемый элементарный объем попадает излучение от всех других элементарных объемов, которое рассеивается в соответствии с показателем σ λ и будет суммироваться с собственным излучением частиц объема.

Величина собственной спектральной плотности мощности теплового излучения от элементарного объема dV = ρdρdφdz ТАО на входе фотоприемника будет определяться выражением [3]

dP₀. = ^k"^A_э M° (ТА е^^л е~^а°^л dVdx dy тг(/₀ + /₃)^{2 V} ’

где а ох и а 1 х = ох + knx — суммарные спектральные показатели ослабления оптического излучения на трассе распространения вне аэрозольного образования и внутри него соответственно [м-1]; М" (Т) = у • Л^ ■ |^е1 /J - 1J — спектральная плотность энергетической светимости абсолютно черного тела с абсолютной температурой T; c 1 и c2 - постоянные Планка; l3 и lо - расстояния от элементарного объема до точки пересечения линии визирования «ФПр – элементарный объем» с условной границей раздела сред ТАО и атмосферы и от точки пересечения до ФПр соответственно.

Для полидисперсной среды с целью учета концентрации и размеров частиц в элементарном объеме можно использовать следующие выражения для определения объемных спектральных коэффициентов рассеяния и поглощения соответственно:

^ = ^j°чх V.^ f V^^^x = ^Jк™х ^ДаУа’ О                                   о

где N - количество частиц в единице объема; к _пчХ ( а ), о ч_х ( а ) - коэффициенты поглощения и рассеяния на частице радиусом a ; f [а ) - функция, описывающая распределение размеров частиц.

Для удобства дальнейшей работы с полученным выражением (1) запишем его для случая единичного объема dV и единичной площади ФПр в виде

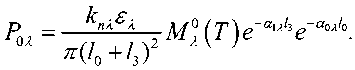
Определим величину потока рассеянной составляющей, попадающей на вход ФПр [4, 5]. На элементарный объем, находящийся на удалении z, будет попадать излучение от всех элементарных объемов ТАО, находящихся как на удалении z 1 < z, так и на удалении z2 > z (рис. 2) [6]. Тогда спектральная плотность мощности излучения элементарного объема, находящегося на удалении z 1 (z2) от ФПр, рассеянного объемом dV, расположенным на удалении z, и попадающего на вход ФПр, может быть определена dp = кпх^х№Д Мо ^Aea'M+h\^p,dp,d(p,dz.dVdxdy-4^2/2(/0+/3)2        7                  1 1 1 1      "

dP. =         М° (TyaiAWVa^p,dp*dz^^^

' 4^/2 (/0+/3)2 Н                            2    „ где }Дб) = —--спектральная индикатриса рассеяния; l1 и l2 - расстояния от элементарных объемов, находящихся на удалении z 1 и z2 от кромки ТАО соответственно до объема dV.

Для единичного объема dV и единичной площади ФПр выражения (4) и (5) запишем в виде dF = кпХ^х№1АМо ^y-avAVh^-^A pdpdV.dz.;

4^²/²(/₀+/₃)^{2 М 7            М М} 1

dp- = ^^L^M4T\e-^w

^+Л 4я-²/²(/₀+/₃)^{2        7                 2}           2

Принимаемая ФПр спектральная плотность мощности излучения всех элементарных срезов ТАО слева (справа) от элементарного объема dV, рассеянного этим элементарным объемом в направлении ФПр, может быть записана в виде выражений z-kz 7л Da(zy)

dPL= J J J dF,:(8)

ZOO

L+La 27rDa(z2)

<, = J J J(9)

z 00

где La – толщина ТАО; Da – высота ТАО.

С учетом полученных выражений (1), (8) и (9) определим суммарную спектральную плотность мощности излучения от единичного элементарного объема dV ТАО на входе фотоприемника с единичной площадью апертуры dPn- = dP" +dP". +R-.                                             (10)

Для определения мощности теплового излучения всего ТАО, принимаемого фотоприемником с апертурой S, необходимо решить интегральное уравнение

Z^- = j Ц JJJ dP_nxpdpd(pdzdx_ndy_ndX,                                (11)

A (S) (П где X 1...X2 = АX - рабочий спектральный диапазон ИК-средства; V - объем ТАО в поле зрения ИК-средства.

С учетом геометрии формируемого полем зрения ИК-средства объема ТАО выражение (11) можно записать в виде z-tex arccos 1--

(S) L 0          0

Для решения расчетных задач в соответствии с полученными выражениями достаточно выразить переменные 1 ₀ , 1 1 , 1 ₂ , 1 3 , 6 1 , 6 ₂ через переменные интегрирования и известные параметры.

Так, в системе координат фотоприемника при условии, что точка приема в начале его системы координат, можно получить

1Л = ^(/xos^9-/}cos#^^;

• /₂ = ^(jOcos^-^cos^J^Gosin^-^sin^J^HT^-^^;

• / =---—----7 =----—•

з /            \ ’ о /\ ’ cos I arctg — I cos I arctg — I с учетом замены переменных x = р•cosф, y = р•sinф

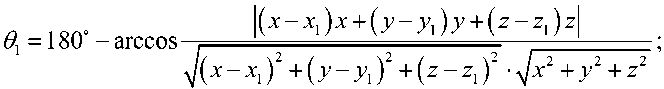
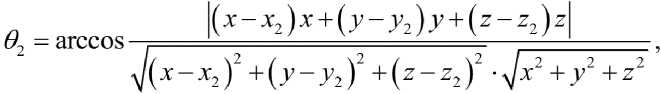
где L – минимальное расстояние от приемника до аэрозольного образования.

На рис. 3 представлены результаты расчетов для типовых условий и следующих исходных данных: рабочий спектральный диапазон ФПр 3–5 мкм; радиус формирующей оптики ФПр 0,03 м; размеры ТАО 30×30×30 м; L =1 км; Т =330 К; ε λ = 0,8; k nλ = 10 ^–3 м ^–1 . Влияние АО как пассивной помехи принято характеризовать коэффициентом пропускания АО T _a ( σ ) [2], который в зависимости от его рассеивающих свойств для указанных исходных данных может принимать значения, представленные на рис. 4.

Результаты анализа полученных зависимостей показывают, что увеличение рассеивающих свойств АО приводит к уменьшению активной помеховой составляющей комбинирован-

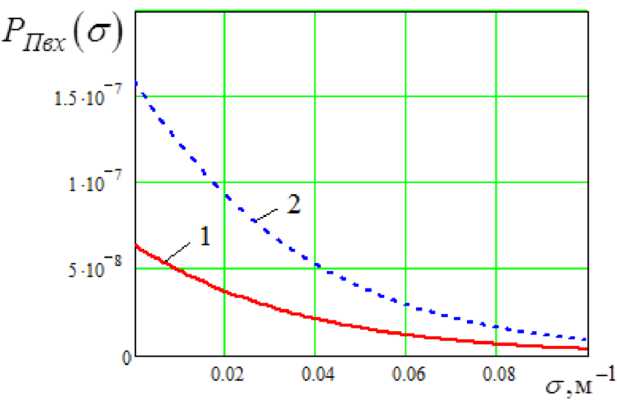
Рис. 3. Зависимости мощности теплового излучения АО на входе фотоприемника от показателя рассеяния его частиц при различных значениях поля зрения фотоприемника: 1 – ω = 2·10 ^–4 ср; 2 – ω = 5·10 ^–4 ср

• Fig. 3.    Dependences of the power of thermal radiation of aerosol formation at the input of the photodetector on the scattering index of its particles at different values of the field of view of the photodetector: 1 – ω = 2·10 ^–4 sr; 2 – ω = 5·10 ^–4 sr

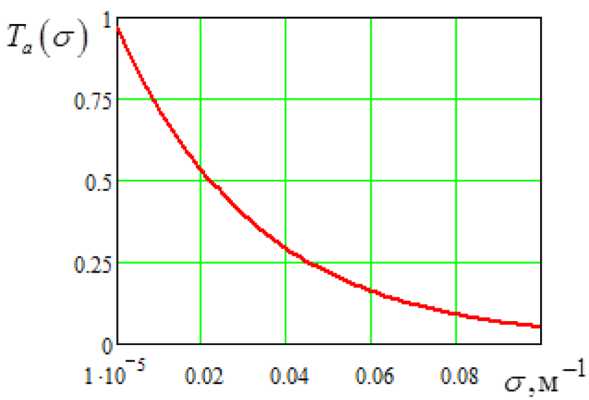
Рис. 4. Зависимость коэффициента пропускания АО от показателя рассеяния его частиц

• Fig. 4.    Dependence of the transmittance of aerosol formation on the scattering index of its particles

ной помехи при одновременном увеличении маскирующего эффекта за счет пассивной помехи [2], что следует учитывать при решении задач по формированию аэрозолеобразующего состава ТАО.

Выводы. Таким образом, разработана модель процессов формирования и распространения в атмосфере ИК-излучения теплоизлучающего аэрозольного образования, позволяющая обосновывать характеристики комбинированных аэрозольных завес в интересах повышения эффективности их применения. На основе введения элементарных объемов и элементарных срезов, включающих элементарные объемы, и использования основных законов образования, поглощения и рассеяния теплового излучения получена система интегро-дифференциальных уравнений, описывающих процедуры формирования ИК-излучения элементарным объемом, молекулярное и аэрозольное (на частицах) рассеяние падающего на рассматриваемый элементарный объем ИК-излучения с других объемов теплоизлучающего аэрозольного образования, переноса прямого (образованного) и рассеянного ИК-излучения от всех элементарных объемов, попадающих на вход приемника ИК-средства.