Модель прогнозного оценивания видимости космического мусора при наблюдении из космоса

Количество космического мусора (далее – КМ) на околоземных орбитах стремительно возрастает и требует контроля [1–8]. КМ занесен в различные каталоги и постоянно отслеживается, но он может сталкиваться с другими объектами, что приводит к возникновению новых объектов КМ и/или смене их траектории, поэтому за ним необходимо постоянное наблюдение. Для наблюдения за объектами необходимо, чтобы они были видимы. Для планирования наблюдения за конкретным объектом КМ или областью необходимо определить время, когда КМ будут освещены солнцем. Анализ научных трудов показал, что подобная проблема не решена для случайно выбранной даты. В данной работе предлагается подход к моделированию освещенности КМ Солнцем, что делает ее актуальной.

Наблюдение за КМ с Земли имеет ряд ограничений, связанных с искажениями атмосферы, облачностью и временем суток. Наблюдение за КМ из космоса лишено данных недостатков, поэтому рассматривается как наиболее эффективная и перспективная система мониторинга.

Расчет возможных параметров КМ, влияющих на возможность обнаружения

Для моделирования оптического обнаружения КМ рассчитывается отраженный от него солнечный свет, блеск которого возможно измерить в виде видимой звездной величины [9; 10]. Данное решение позволяет оценить видимость КМ с заданными параметрами оптической системы. Возможности наблюдения КМ характеризуются наблюдаемой

звездной величиной КМ, которая связана с расстоянием до него соотношением

m = - 26,85 - 2,5log₁₀

' x d^F^ '

4 R ²

\             7

,

где d - диаметр поперечного сечения КМ; у - коэффициент отражения; R -расстояние до КМ; F (ф) - фазовая функция,

F (ф) = —2((п - ф)cos (ф) + sin (ф));

3п

ф - угол освещения КМ Солнцем [10].

Взаимосвязь угла освещения КМ Солнцем и его видимой звездной величины для диаметра поперечного сечения КМ 1,5 м и коэффициента отражения КМ 0,5 на удалении в 1000 км приведена в Таблице.

Таблица

Зависимость видимой звездной величины от угла освещения

m	4,98	5,00	5,11	5,27	5,51	5,81	6,21	7,37	8,26	45,99
φ	10	15	30	45	60	75	90	120	135	180

Источник: таблица составлена авторами на основе выражений (1) и (2).

Модель прогнозного оценивания видимости космического мусора при наблюдении из космоса

Анализ таблицы показывает, что угол освещения КМ Солнцем при прочих равных значениях во многом влияет на его обнаружение и требует обязательного учета при моделировании.

Теоретический расчет угла освещения космического мусора Солнцем

Приведенное ранее выражение требует знания угла, под которым выбранный объект КМ или область пространства освещены Солнцем. Но возникает сложность в определении положения Солнца, поскольку это связано с расчетом точной даты [11] и последующим переводом полученных координат, поскольку для правильного расчета все объекты должны быть привязаны к единой координатной системе. Для этого следует выполнить ряд шагов.

• 1.    Расчет долготы перигелия (ω). Перигелий – это точка на орбите Земли, ближайшая к Солнцу. Его долгота изменяется со временем из-за прецессии земной орбиты. Для расчета долготы перигелия на заданную дату можно использовать формулу

• 2.    Расчет средней аномалии M . Средняя аномалия представляет собой угол между перигелием и текущим радиус-вектором Земли, измеренный в плоскости орбиты, и рассчитывается по формуле

• 3.    Расчет эксцентрической аномалии E . Эксцентрическая аномалия связана со средней аномалией M и эксцентриситетом орбиты Земли. Определяется из уравнения Кеплера, которое выражает баланс между гравитационной силой и центростремительной силой в плоскости орбиты. Уравнение Кеплера выглядит следующим образом:

ω = ω0 + (ωdotD), где ω0 – долгота перигелия на начальную дату; ωdot – скорость прецессии перигелия (градусы в день); D – количество дней от начальной даты.

M = M ₀+ ( nD ),                              (3)

где M₀ – средняя аномалия на начальную дату; n – среднее движение (градусы в день); D – количество дней от начальной даты.

M = E – e⋅sin(E), где M – средняя аномалия для заданного момента времени; E – эксцентрическая аномалия, которую нужно найти; e – эксцентриситет орбиты Земли.

Для нахождения эксцентрической аномалии E из уравнения Кеплера обычно используются численные методы, такие как метод Ньютона или метод деления пополам. Один из самых распространенных методов – это метод Ньютона, который использует итерационный процесс для нахождения корней уравнения.

Процесс нахождения эксцентрической аномалии методом Ньютона выглядит следующим образом.

Начальное приближение . Выбирается начальное приближение для эксцентрической аномалии E. Это может быть любое значение, но обычно выбирается значение, близкое к средней аномалии M.

Итерационный процесс. Повторяются следующие шаги до достижения необходимой точности:

• •    вычисляется значение функции f ( E ) = E - e ⋅ sin( E ) и ее производной f′ ( E ) = 1 -e ⋅ cos( E );

• •    корректируется значение эксцентрической аномалии по формуле

  
  

новое старое          старое          старое ;

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

• •    проверяется достижение необходимой точности; если условие точности выполнено, то процесс завершается, и найденное значение эксцентрической аномалии считается конечным результатом.

• 4.    Расчет эклиптических координат λ и β. Эклиптические координаты λ и β Солнца могут быть рассчитаны из долготы перигелия ω, средней аномалии M и эксцентрической аномалии E с использованием следующей формулы:

• 5.    Радиус-вектор (расстояние до Солнца). Радиус-вектор r представляет расстояние от Земли до Солнца. Для его расчета можно использовать формулу

• 6.    Истинная аномалия. Истинная аномалия v – угол между перигелием (точкой на орбите, ближайшей к Солнцу) и радиус-вектором Земли, измеренный в плоскости орбиты. Рассчитывается с помощью формулы

Этот процесс повторяется до тех пор, пока разница между последовательными значениями эксцентрической аномалии не станет меньше заданной точности. Полученное значение эксцентрической аномалии E затем используется в дальнейших расчетах для определения эклиптических координат.

Λ = M + (2e ⋅ sin( M )) + ω, (5) где e – эксцентриситет орбиты Земли; β = 0

Используя эти формулы, можно рассчитать эклиптические координаты Солнца на заданную дату. Эти координаты позволяют определить положение Солнца на эклиптике в заданный момент времени.

r = a (1 - e2)/(1 + e ⋅ cos(v)), (6) где a – большая полуось орбиты Земли; e – эксцентриситет орбиты; v – истинная аномалия.

tan(v/2) = 1 - e1 + e ⋅ tan( E /2), (7) где E – эксцентрическая аномалия.

Для преобразования эклиптических координат λ, β Солнца в экваториальные координаты x , y , z в экваториальной геоцентрической системе координат можно воспользоваться преобразованиями, основанными на углах наклона небесной сферы.

А) Вычисление прямого восхождения (RA) и склонения (Dec). Прямое восхождение (RA) и склонение (Dec) являются экваториальными координатами, определяющими положение объекта на небесной сфере:

RA = arctan2(sin(λ) ⋅ cos(ε) - tan(β) ⋅ sin(ε),cos(λ)); (8)

Dec = arcsin(sin(β) ⋅ cos(ε) + cos(β) ⋅ sin(ε) ⋅ sin(λ)), (9) где λ – эклиптическая долгота Солнца; β – эклиптическая широта Солнца; ε – наклон эклиптики к экватору Земли.

Б) Преобразование в декартовы координаты. Полученные RA и Dec являются сферическими координатами. Для преобразования их в декартовы координаты ( x , y , z ) можно воспользоваться следующими формулами:

x = cos(RA) ⋅ cos(Dec); (10)

y = sin(RA) ⋅ cos(Dec); (11)

z = sin(Dec). (12)

После применения этих формул получим координаты Солнца в экваториальной геоцентрической системе координат, где ось x направлена к весеннему равноденствию, ось y находится в направлении прямого восхождения 90 град от весеннего равноденствия, а ось z направлена в сторону полюса Земли.

Модель прогнозного оценивания видимости космического мусора при наблюдении из космоса

Моделирование угла освещения космического мусора Солнцем

Для упрощения расчетов на языке программирования Python была разработана программа, в которой формируется трехмерное пространство: в нулевых координатах размещается Земля, около нее размещается космический аппарат-наблюдатель и объект КМ, положение которых задается с помощью кеплеровых элементов орбиты, Солнце, положение которого определяется с учетом дат по Юлианскому календарю. Затем производятся требуемые расчеты.

Основными этапами расчетов являются:

• •    расчет времени;

• •    расчет положения космических объектов (аппарат-наблюдатель и КМ);

• •    преобразование кеплеровых элементов в прямоугольные координаты XYZ ;

• •    формирование функции для вычисления угла между двумя векторами;

• •    вычисление угла освещенности КМ Солнцем с космического аппарата-наблюдателя по выражению (2);

• •    расчет наблюдаемой звездной величины по выражению (1).

Проверка работоспособности кода

По результатам работы программы получаем значения положения Солнца и искусственного спутника Земли относительно Земли, а также значения углов освещенности заданного КМ (см. Рисунок).

Данные относительно угла обзора и видимой звездной величины выводятся в командной строке:

«Угол освещенности космического мусора Солнцем относительно КА наблюдателя: 155,59 градусов».

«Видимая звездная величина КМ при наблюдении с КА наблюдателя 11,23 m».

Адекватность полученных значений была проверена для искусственно заданных значений положений Солнца, космического аппарата-наблюдателя и КМ с использованием специального программного обеспечения Satellite Toolkit 8.0, расхождение полученных значений менее 0,1 %.

Таким образом, адекватность программы и заложенных в нее моделей подтверждена.

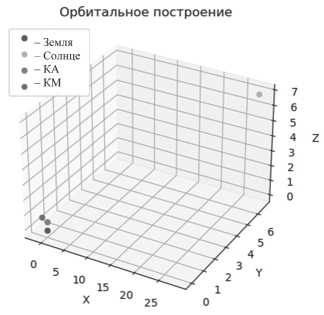
Рисунок. Пример графической отработки программы Источник: рисунок выполнен авторами.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

Заключение

Моделирование и расчет угла освещенности КМ являются важной научной задачей, а предложенный аппарат позволяет быстро и с достаточной точностью получить данные значения для выбранного времени. Однако следует учитывать, что при рассмотрении данной модели не учитывается влияние отраженного от Луны света, который может «ослепить» оптическую систему, а также то, что в процессе движения КМ по орбите вокруг Земли периодически могут возникать ситуации, когда КМ попадает в тень Земли, что приводит к резкому падению освещенности. Учет влияния данных факторов является направлением дальнейшего совершенствования модели.