Модель проверки знаний учащихся при проведении онлайн-тестирования

Главная цель системы высшего образования заключается если не в подготовке сложившегося специалиста, способного эффективно решать задачи, возникающие в ходе профессиональной деятельности, то хотя бы в том, чтобы дать студенту достаточный набор знаний и навыков, которые позволили бы ему стать таковым, набравшись практического опыта. Поэтому, получив на входе выпускников школ, стремящихся поступить хотя бы куда-нибудь, ВУЗы должны обеспечить такое качество учебного процесса, чтобы через четыре, пять или шесть лет на выходе не получить того же самого школьника, но уже с дипломом о высшем образовании. Для этого необходим тщательный контроль качества образовательного процесса, и одним из элементов этого контроля является регулярная оценка уровня знаний, умений и навыков студентов (как, впрочем, и абитуриентов, ведь нельзя получить что-то из ничего). Ранее основные проверки знаний производились при поступлении (вступительные экзамены), при сдаче экзаменов в конце каждого семестра (экзаменационные сессии), а также при сдаче государственных экзаменов (ГОСов). Кроме того, произошла реформа системы высшего образования, состоящая в переходе к двухступенчатой системе подготовки специалистов (4 года – бакалавр, 2 года – магистр) и реализации принципа образовательной мобильности, при котором, отучившись 4 года в одном ВУЗе и получив диплом бакалавра, студент может поступить в магистратуру другого

ВУЗа. По этой причине возникает дополнительная необходимость проверки знаний учащихся – при переходе из бакалавриата в магистратуру. Многие ВУЗы, особенно престижные, из года в год сталкиваются с ситуацией, когда число мест в магистратуре значительно уступает числу желающих их занять, ведь помимо «родных» выпускников бакалавриата на эти места претендуют выпускники и других ВУЗов. Возникает проблема, как не ошибиться в выборе, или, как это было сформулировано давным-давно, проблема отделения зерен от плевел. В связи с огромным потоком поступающих вызывает большие сомнения целесообразность и эффективность прямого человеческого (ручного) контроля знаний – процесс этот трудоемкий и монотонный, а количество отведенного на него времени весьма ограничено. Некоторые ВУЗы в рамках процессов инноватизации и информатизации образования переходят к использованию онлайн-систем тестирования и проверки знаний абитуриентов. Однако при этом большую значимость обретает вопрос вероятности совершения ошибки проверки знаний или ошибки классификации, при которой негодный абитуриент признается годным, а годный в свою очередь признается негодным. И если в нашем отечестве пока мало кто слышал об абитуриентах, подающих в суд на ВУЗ, например, из-за грубых ошибок в тестовых заданиях, то на проклятом Западе это уже давно не новость.

Ошибки при проверке знаний учащихся в ходе онлайн-тестирования могут быть обусловлены самыми разными факторами, например, двусмысленной постановкой задания теста или же нестандартной записью ответа тестируемым. Оба приведенных варианта не были бы актуальны в случае обычной процедуры сдачи экзамена, предполагающей непосредственное общение учащегося с экзаменатором, но в случае с онлайн-тестированием они вполне вероятны. Еще одним фактором, как лично убедились авторы при проведении математической интернет-олимпиады для поступающих в магистратуру СПбГЭТУ «ЛЭТИ» по направлению «Системный анализ и управление», являются ошибки, образующиеся по принципу «испорченного телефона». Как правило, разработкой тестовых заданий занимаются одни, а их переносом в электронную среду тестирования знаний – другие. При этом последние часто далеки от предметной области, к которой относится содержание теста, поэтому могут вносить (и, к сожалению, вносят) ошибки в исходное содержание теста, вызванные непониманием транслируемого материала. Особенно часто подобная ситуация возникает, когда тест содержит значительное число математических заданий в соответствующей нотации, незначительное отклонение от которой легко может привести к полному изменению исходного смысла или его потере. И это не говоря уже о простых опечатках или случайных сбоях в работе систем онлайн-тестирования. Поэтому была сделана попытка формализовать и математически описать проверку знаний учащихся с целью снизить влияние ошибок различной природы на ее результат. При этом следует отметить, что предложенная модель может быть использована не только в образовательной сфере и вполне может быть адаптирована для моделирования решения задач классификации в различных областях.

Методология

Рассмотрим некоторый объект, который может находиться в одном из состояний A1, A2,..., An . При этом производится одна (или несколько) проверок относительно установления состояния, в котором данный объект находится. В данном случае под объектом понимается тестируемый, уровень знаний которого подлежит определению. Соответственно, различным уровням знаний отвечают различные состояния тестируемого. Так как чем выше уровень знаний, тем лучше, то будем полагать, что все состояния упорядочены следующим образом Ai х A2 х ... х An , т.е. со- стояние A1 является наилучшим (например, тестируемый успешно справился со всеми заданиями теста), а состояние An - наихудшим (тестируемый провалил тест).

Считаем, что проверка не является безошибочной, и возможна ошибка классификации, когда объект, истинное состояние которого A k , в результате проверки ошибочно классифицируется как объект в состоянии A m [1, 2, 3, 4]. Поэтому характеристики процедуры проверки можно представить в виде следующей матрицы контроля, каждый элемент которой представляет собой вероятность классифицировать объект, находящийся в i -ом состоянии, как объект, находящийся в j -ом состоянии:

^К11 К 12 . . . ^К1 n

КА

21 ^JV22 . . . ^JV2 n

К =

А. Д'            К

V n1   nxH2   . . . nxnn у и которая, в соответствие с [1], отражает все особенности процедуры проверки (классификации объектов). Как несложно видеть, матрица (1) является стохастической,

n т. к. выполняется известное соотношение Ку > 0,

^ К у = 1. Именно это свойство j = 1

матрицы (1) и служит причиной рассмотренной далее методологической ошибки. Предположим, проводится r проверок подряд, каждая из которых может быть описа на соответствующей матрицей контроля: К11 K1l2

^К 21 К 2 2

К I =

К \ К1-) к1

V ^V n 1     ^±хи 2     . . . n^xnn у

Тогда в качестве результирующей матрицы контроля, комплексирующей все процедуры проверки, зачастую выбирают матрицу, равную произведению матриц контроля всех проведенных проверок:

r

К = п К 1                          (3)

I = 1

Основной причиной такого выбора выступают те соображения, что матрица (3) также является стохастической, и, вообще говоря, является результирующей матрицей для последовательного использования набора стохастических матриц.

Методологическая ошибка использования матрицы (3) заключается в том, что на самом деле каждая следующая процедура проверки не использует результаты предыдущей проверки, т. е. не контролирует результаты предыдущей проверки, а независимо определяет, в каком из возможных состояний находится объект. Таким образом, использование матрицы (3) для моделирования комплекса последовательных проверок, т. е. комплекса проверок, имеющего линейную структуру, является некорректным. Тот факт, что решение о классификации объекта в данном случае принимается после проведения фактически дублирующих друг друга проверок, означает, что, при отсутствии дополнительных условий, результирующей является только последняя проверка. Следует еще раз уточнить, что это справедливо только для случая, когда комплекс проверок имеет простейшую линейную структуру, т.е. процеду-

ры проверки выполняются последовательно и не влияют друг на друга.

Для ряда частных случаев реализации структуры комплекса проверок на основе использования принципов обобщенного структурного метода [1, 5] в [2, 6] по-

лучены конкретные аналитические выражения.

Для развития модели определим некоторые дополнительные понятия.

Будем считать, что процедура проверки идеальна , (невозможны ошибки

классификации, если соответствующая матрица контроля является единичной:

' 1    0    .    .   .0

0   1   0   .   .0

0   0   1   .   .0

( 0 0

Будем считать, что процедура проверки является оптимистичной , если вы-

полняются следующие соотношения:

К у >  0, если i >  j,

n                                 (5)

К у = 0, если i <  j, £ К у = 1.

j = 1

Выполнение (5) означает, что процедура проверки допускает только те ошибки классификации, при которых происходит завышение оценки уровня знаний тестируемого. В таком случае матрица контроля будет треугольной (поддиагональной) и иметь вид:

	' К 11      0    . . 0    0
	К 21   К 22   . . 0   0
К (О) =	.    .   ...   0 .     .   ...    .	.                             (6)
	.    .   ...   0
	V Кп 1 Кп 2    . .   . Кпп J

Будем считать, что процедура проверки является пессимистичной , если выполняются следующие соотношения:

K ij >  0, если i <  j,

K ij = 0, если i >  j , £ К у = 1. j = 1

Выполнение (7) означает, что процедура проверки допускает только те ошибки классификации, при которых происходит занижение оценки уровня знаний тестируемого. В таком случае матрица контроля будет треугольной (наддиагональной) и иметь вид:

	^ К 11	К 12      .     .	. К 1 n '
	0	К 22     .     .	. К 2 n
К (П) =	0	0    К 33 .	. К 3 n

I 0     0      .    . . K nn J

Назовем процедуру проверки принадлежащей классу безошибочности 1–γ, если сумма всех элементов (не включая диагональный элемент) каждой из строк матрицы контроля данной процедуры не превосходит по величине значение γ. Данное требование может быть представлено в виде условия вида Кц >  1 -у . Параметр у задает верхнюю границу для суммы вероятностей возможных ошибок классификации.

Как уже отмечалось ранее, все возможные состояния упорядочены по убыванию их предпочтительности от лучшего – A ₁ , до худшего – A_n . Очевидно, что тогда чем ближе в этом ряду находятся два состояния, тем сильнее они «похожи», и тем выше вероятность перепутать их между собой. Если предположить, что процедура проверки не предполагает грубых ошибок классификации, при которых происходит путаница между далекими друг от друга состояниями объекта проверки, то можно считать, что матрица контроля будет иметь следующий ленточный вид:

	' К 11	К 12	0	.	.	0 '
	К 21	К 22	К 23	.	.	0
К =	0 .	К 32 .	К 33 .	К 34 .	. .	0 .	.                        (9)
	.	.	.	.	К п - 1 п - 1	К п - 1 п
	ч 0	0	.	.	К пп - 1	К пп >

Таким образом, если процедура проверки является оптимистичной, и при этом отсутствуют грубые ошибки, то матрица контроля будет иметь следующий вид:

	' К 11	0	0	.	.	0 Л
	К 21	К 22	0	.	.	0
К (О) =	0 .	К 32 .	К 33 .	. .	. .	0 .	.               (10)
	.	.	.	К п - 1 п - 2	К п - 1 п - 1	0
	. 0	0	.	.	К пп - 1	К пп ?

Если при этом процедура проверки относится к классу безошибочности 1–γ, то для недиагональных элементов матрицы проверок выполняются соотношения вида К - 1 i < у .

Аналогично, если процедура проверки является пессимистичной, и отсут-

ствуют грубые ошибки, то К(П) = матрица контроля примет вид: ' К11  0  0.     . К21  К22    0        .          . 0К32  К33       .          . ...   .   . 0 Л 0 0 . . (11) Как и в предыду . .0 ем . 0 случае, .    Кп-1 п -2 Кп-1 п-1 .          .         Кпп-1 если процедура проверки 0 Кпп > отно сится к классу безошибочности 1–γ, то для недиагональных элементов матрицы проверок выполня- ются соотношения вида Ki ,+i < у .

Введем понятие мажорирующих матриц контроля для процедур проверки, принадлежащих классу безошибочности 1–γ и имеющих матрицы контроля вида (10) и (11). Будем считать, что матрица контроля является мажорирующей снизу для всех матриц оптимистичного контроля, принадлежащих классу безошибочности 1–γ, если все ее недиагональные элементы равны γ, т. е. такая матрица контроля будет иметь вид:

' 1  0  0.0  0

Y 1-Y 0.00

К (O,1-Y) =0    Y    1-Y   .    0     0 .(12)

.                   .                         .                   .                   ..

.     .       .     Y  1-y0

1 0    0     .    .     Y     1 -yJ

Как несложно видеть, мажорирующая матрица (12) является наихудшей матрицей в классе безошибочности 1–γ.

Аналогично будем считать, что матрица контроля является мажорирующей снизу для всех матриц пессимистического контроля, принадлежащих классу безошибочности 1–γ, если все ее недиагональные элементы равны γ, т. е. такая матрица контроля будет иметь вид:

p -y   y .    .   0   0 ) 01 -y Y .  0  0 К «Ч-» =   0   01 -y Y    .  0 . .                         .                         .                   .                   .                   .

(13)

.        .        .      . ^{1 -y Y}

( 0  0   .  .01 J

Как и в предыдущем случае, мажорирующая матрица (13) является наихудшей матрицей в классе безошибочности 1–γ.

По аналогии с мажорирующими матрицами вида (12) и (13) можно попробовать определить вид мажорирующей матрицы для всех процедур проверки, не допускающих грубых ошибок. Очевидно, что никакая из матриц вида (9), принадлежащих классу безошибочности 1–γ, не может, в отличие от матриц (12) и (13), являться наихудшей в данном классе. Таким образом, можно говорить о некоторой приближенной матрице контроля, которая в среднем будет давать наименьшее отклонение. В качестве такой матрицы контроля может быть использована матрица следующего вида:

	1 -y Y 0     .     0     0 Y
	Y/2 1 -y y/ 2    .     0     0
К (1 -y ) =	0 y /2 1 — Y Y/2 .     0 ......	.                      (14)
	.       .       .      Y/ 2 1 — Y Y/2
	^ 0      0      .       .       y 1 — Yj

Использование модели на практике

Одним из возможных подходов к повышению надежности результата проверки знаний в ходе онлайн-тестирования заключается в двухкратном прохождении испытуемым процедуры проверки. При совпадении результатов каждой из независи- мых проверок, когда обе независимые процедуры проверки классифицировали испытуемого одинаково, результат считается достоверным и принимается. В противном случае испытуемому, результаты которого вызвали сомнения, дается возможность пройти проверку еще раз. Для практического применения подобного подхода не обязательно заставлять каждого испытуемого дважды проходить тест, а потом сравнить результаты. В психологии уже давно многие тесты содержат «дублирующие» вопросы, сравнение ответов на которые позволяют исследователю сделать выводы об их искренности. Аналогично содержание теста для проверки знаний может незаметно для тестируемого разбито на две одинаковых с точки зрения проверяемых знаний и навыков части (а при необходимости - и более двух). Сравнение результатов проверки каждой из таких частей теста позволяет сделать вывод об однозначности классификации тестируемого по уровню его знаний.

Рассмотрим некоторый частный случай, когда конечным результатом такой двойной проверки является принятие либо некоторого положительного, либо некоторого отрицательного решения. При этом будем предполагать, что известны вероятности (возможно, приближенные) распределения контингента проверяемых по уровням знаний. Тогда каждый из проверяемых (тестируемых) может быть годным с вероятностью а - положительное решение в случае идеальной процедуры проверки, или же негодным с вероятностью (1-а) - отрицательное решение в случае идеальной процедуры проверки. Очевидно, что вероятность завершения двойной проверки с первого 2    2

раза равна (1 - у ) + y . Для подобной двойной процедуры проверки можно построить схему ее выполнения, приведенную на рис. 1, воспользовавшись обобщенным структурным методом.

Необходимо заметить, что и результаты обеих независимых проверок могут оказаться ошибочными. Это может быть обусловлено теми же факторами, что уже ранее рассматривались в данной статье, однако в силу того, что рассматриваемая проверка знаний носит двухкратный характер, вероятность ошибки классификации даже в самом плохом случае будет в несколько раз меньше.

Для удобства введем следующие обозначения:

А - тестируемый является годным;

В - тестируемый является негодным;

A i - тестируемый признан годным (соответствующим некоторому набору требований) по результатам i -й двойной проверки;

B i - тестируемый признан негодным (несоответствующим некоторому набору требований) по результатам i -й двойной проверки;

C i -по результатам i -й двойной проверки ничего сказать нельзя и тестируемый отправлен на следующую проверку;

A_i / А - тестируемый признан годным (соответствующим некоторому набору требований) по результатам i -й двойной проверки и при этом он и является годным;

A i / В - тестируемый признан годным (соответствующим некоторому набору требований) по результатам i -й двойной проверки, но при этом он является негодным (ложный пропуск);

B i / В - тестируемый признан негодным (несоответствующим некоторому набору требований) по результатам i -й двойной проверки и при этом он и является негодным;

B i / А - тестируемый признан негодным (соответствующим некоторому набору требований) по результатам i -й двойной проверки, но при этом он является годным (ложная выбраковка);

C i / А - i -я двойная проверка ничего не выявила и годный тестируемый отправлен на следующую проверку;

C i / В - i -я двойная проверка ничего не выявила и негодный тестируемый отправлен на следующую проверку.

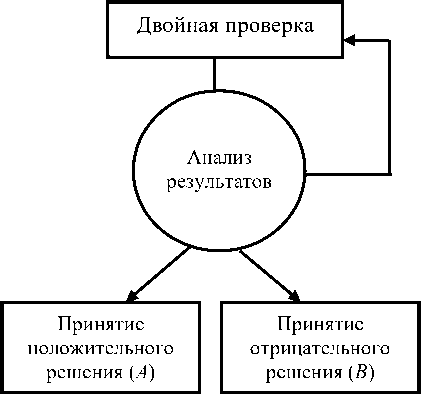
Повтор двойной проверки из-за несовпадения результатов

Рис. 1. Схема проведения двойной проверки знаний

Для оценки качества (надежности) полученного результата проверки знаний можно использовать следующие вероятности:

Р ( А / А ) - вероятность того, что тестируемый правильно признан годным по результатам всего процесса тестирования (доля годных среди признанных годными): cxH-v')²

P ( A / A ) = а ^ P ( A i / A ) = а (1 - у )² 2 (2 у - 2 у ²) i =    ⁽ 22 ;

i = 1                          i = 0                  (1 - у ) + у

Р ( А / В ) - вероятность того, что тестируемый ошибочно признан годным по результатам всего процесса тестирования (доля негодных среди признанных годными):

П-П?)у2

P(A / B) = (1 - а)2 P(A / Bi) = (1 — а)у2 2 (2у - 2у2)1 = ( i=1                          i=0                  (1 71 +У

Р ( В / А ) - вероятность того, что тестируемый ошибочно забракован (доля ошибочно забракованных):

”                 ”r/v2

P(B / A) = а2 P(Bi / A) = ау2 2 (2у - 2у2)i =-----^2

i = 1                    i = 0                  (1 - у ) + у

Р ( В / В ) - вероятность того, что тестируемый правильно признан негодным по результатам всего процесса тестирования (доля правильно забракованных):

P ( B / B ) = (1 - а ) 2 P ( B i / B ) = (1 - а )(1 - у )² ] ” (2 у - 2 у ²) i = ⁽¹ -^{а )(} 1 -^ . i = 1                             i = 0                 (1 -у )² +у ²

Для иллюстрации получения приведенных вероятностных оценок можно построить следующее дерево вероятностей (рис. 2):

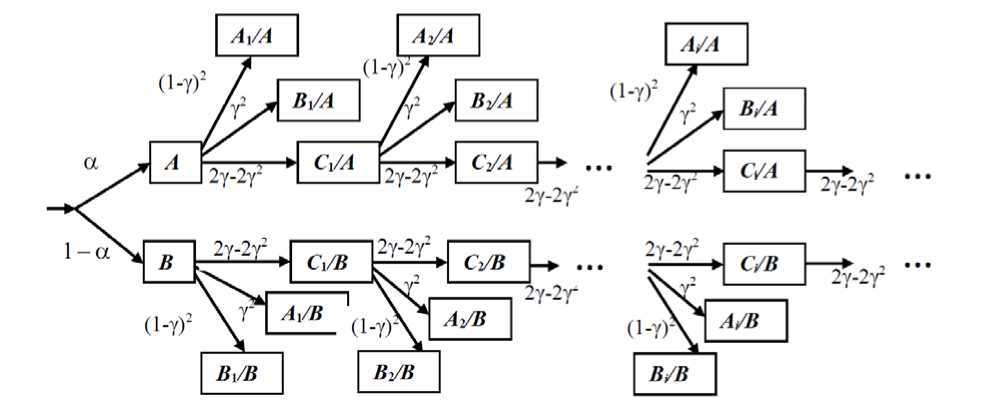
Рис. 2. Дерево вероятностей

Заключение

Представлена вероятностная модель, позволяющая описывать проведение комплексных процедур проверки знаний студентов, в частности, при проведении онлайн-тестирования. Описаны базовые положения модели, приведен вариант ее применения при использовании двойной независимой проверки. Предложенная модель помимо образовательной сферы может быть весьма полезна и при решении других задач классификации.