Модель рабочей памяти продукционной системы, предназначенной для автоматического извлечения знаний из текстов

Эффективность продукционной системы, особенно с большим объемом правил, очень сильно зависит от эффективности механизма управления продукциями. В исследуемой продукционной системе для решения данной проблемы используется алгоритм Rete [3] сопоставления фактов с шаблонами правил и определения правил, условия которых удовлетворены на текущем состоянии рабочей памяти [1]. Немалую роль при этом играют организация рабочей памяти и механизм ее формирования. В процессе функционирования продукционной системы рабочая память должна содержать факты, отражающие текущее состояние решения задачи. Кроме того, она должна быть согласована с множеством продукционных правил [2]. В данной работе рабочая память должна инициализироваться фактами, описывающими знания о предложении словарной статьи терминологического словаря на естественном языке. То есть заполнение рабочей памяти должно производиться в результате компьютерного анализа текста на естественном языке. Несмотря на все богатство разработанных на сегодня теоретических положений в области анализа текста, сложность заключается в отсутствии практических реализаций. Особенно сложными для реализации являются синтаксический и семантический анализы. Все вышесказанное определило необходимость решения задачи построения рабочей памяти для продукционной системы извлечения знаний. Для этого был выполнен анализ существующих систем продукций, реализующих методы естественно-языковой обработки текста, что позволило определиться со структурой рабочей памяти и подходом к ее формированию и на основе полученных результатов разработать прототип программного обеспечения, выполняющего заполнение рабочей памяти на основе естественно-языкового анализа текста. В предлагаемой статье приведены результаты выполненных исследований.

Система продукций

Для начала рассмотрим основные компоненты интеллектуальной системы, основанной на правилах. На рисунке 1 представлена обобщенная схема модуля управления продукционными правилами.

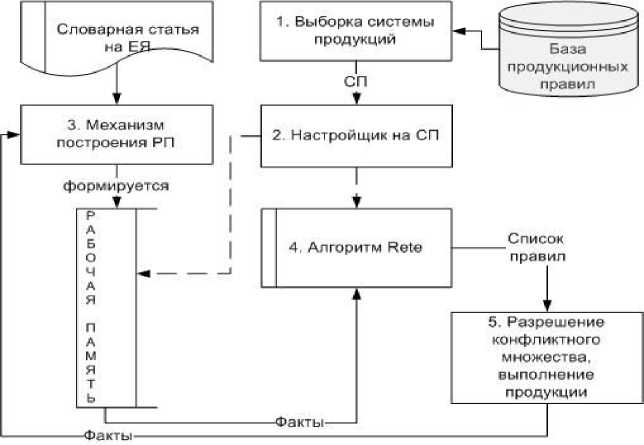
Рис. 1. Схема модуля управления продукционными знаниями

База правил содержит методы естественно-языковой обработки текста в виде продукционных правил морфологического анализа, выделения устойчивых словосочетаний и извлечения знаний. Продукционное правило определяется упорядоченной тройкой множеств

П = ( С , A, D¹) , где С - условие правила;

A - множество добавляемых правилом фактов;

D - множество удаляемых правилом фактов.

Для записи элементов основных конструкций языка правил используется язык исчисления предикатов первого порядка. Каждое из множеств С, A , D представляет собой множество атомарных формул языка исчисления предикатов первого порядка. При этом фактами называются атомарные формулы исчисления предикатов первого порядка без свободных переменных [2]. В правилах атомарные формулы из множеств С, A , D превращаются в факты в процессе применения правила. Под применением понимается подстановка ( m i ,m 2 , к , m n ) на места свободных переменных ( x i ,x 2 , к , x n )и проверка для каждой формулы P ( x i , x 2 , к , x n ) из множества С выполнимости условия в текущем состоянии рабочей памяти. Условие правила выполнено, если в текущем состоянии рабочей памяти истинна каждая из атомарных формул условия. Правило применимо к состоянию рабочей памяти, если его условие выполнено в этом состоянии. Для проверки применимости продукционного правила к рабочей памяти в данной работе используется алгоритм Rete, являющийся самым эффективным алгоритмом сопоставления с образцом [3].

Рабочая память согласно [2] должна обладать следующими свойствами:

• -    правило рассматривается как действие или команда исполнительному органу;

• -    команда может разворачиваться в последовательность действий;

• -    добавляемые или удаляемые факты, называемые эффектом действия, выполняют модификацию модели мира, т.е. формируют в рабочей памяти системы отражение тех изменений в мире, которые произошли после выполнения действий, предписанных правилом;

• -    правила могут рассматриваться и как средство пополнения знаний о мире.

Рабочая память должна быть согласована с множеством правил. Если имеется некото-N рое множество правил 0 = {Пii = 1, N} и Q = U Ci u Ai u Di - объединения условий, мно-i=1

жеств добавляемых фактов и множеств удаляемых фактов по всему множеству 0 , M - множество индивидов предметной области, тогда для каждой n- местной атомарной формулы P ( x 1 ,x 2 , к , x n ) e Q рабочая память должна содержать n- местное конечное отношение I ( P ) с M n , где I - интерпретирующее отображение. На рисунке 2 стрелками показаны примеры отображения I для одно-, двух- и трехместных формул.

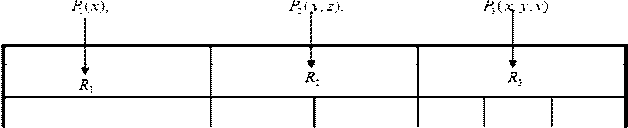
Рис. 2. Интерпретирующее отображение

Таким образом, рабочая память должна содержать множество конечных отношений или таблиц, каждая из которых является интерпретацией одного из предикатных символов, входящего в Q . Построим модель рабочей памяти нашей продукционной системы в соответствии с вышеизложенными положениями.

Модель рабочей памяти

Построение рассмотрим на примере анализа системы продукций, предназначенной для извлечения семантического отношения «часть - целое» 0 W = { П _; | i = 1,16}. Каждое правило данной системы имеет вид П i = { C i , A i }, i = 1,16.

В статье для примера приведем правило П 1 = { C 1 , A 1 }, где множество D 1 = 0 *, а множества C и A 1 имеют вид:

С 1 = { PAggrWhole ( p1, k 1), PAggrWhol e( k 1, s 1), PAggrWhol e( k 1, s 2), PAggrWhol e( s 1, l 1)

PAggrWhole(s1," часть"),PPropCharacter(11,"именительный падеж"),PAggrWhole(k 1, s2), PAggrWhole(s2, z1), PPropCharacter(z1, "родительный падеж")} и A1 = {PHierCategory(z1,"Целое"),PHierCategory(l1,"Часть")}.

Множество объединений условий, множеств добавляемых фактов и множеств удаляемых фактов Q wp по всему множеству © wp содержит предикаты четырех видов: PAggrWhole ( x , y ), PPropCharacter ( x , y ), PHierIndex ( x , y ) и PHierCategory ( x , y ). Ниже приведен фрагмент множества Q wp :

0 _WP = { PAggrWhole ( p 1, k 1), PAggrWhol e( k 1, s 1),..., PAggrWhol e( s 1," часть"),

PAggrWhol e( s 1," элемент"), PAggrWhole ( p 1, q1), PAggrWhole ( r 1,"включает"),

PAggrWhole (г1,"в себя"),..., PPropCharacter ( z 1," винительный падеж"),

PHierIndex (r1, '1'),..., PHierCategory ( z 1," Целое"), PHierCategory ( 1 1," Часть"),...}

Здесь атомарная формула PAggrWhole(x,y) означает, что элемент текста x находится в отношении агрегации «целое - часть» с элементом y. Элемент текста x является целым, а элемент y - частью x. Объектами анализа текста могут быть предложение, словосочетание, семантическое отношение, лексема, заголовочный термин. Если объектом анализа является предложение, то в отношении агрегации «Целое-Часть» могут находиться: <предложение -лексема>, <предложение - композиционное словосочетание>, <предложение - словосочетание>, <предложение - семантическое отношение> [1].

В атомарной формуле PPropCharacter ( x , y ) предикатный символ PPropCharacter указывает на то, что элемент текста x имеет характеристику (свойство) y . Если объектом анализа является лексема, то к характеристикам лексемы может относиться набор параметров, приписанных данной словоформе: часть речи, в зависимости от части речи - падеж, род, число, время или лицо.

Атомарная формула PHierIndex(x,y) означает, что элемент текста x имеет некоторый порядковый номер у . Если рассматривать предложение, то к элементам текста x , имеющим порядковый номер, который определяет их положение в предложении относительно других элементов, относятся лексема, словосочетание, семантическое отношение.

Формула PHierCategory ( x , y ) означает, что элемент текста x относится к категории у . Например, некоторая выделенная лексема предложения является целым или родовым понятием или синонимом по отношению к другой лексеме или группе лексем. Данная формула принадлежит множеству добавляемых фактов продукционного правила, т.е. определяет некоторое заключение продукционного правила.

Множество индивидов предметной области M wp будет содержать результаты лингвистического анализа текста, т.е. факты, описывающие знания о единицах анализируемого текста. Например, при анализе предложения «Процессор - это часть современного компьютера» M wp будет содержать факты вида PAggrWhole ( " Процессор - это часть современного компьютера " , " Процессор " ).

Таким образом, для рассматриваемой системы продукций, интерпретирующее отношение I можно задать следующим образом:

• I :    P « R ,

где P - множество предикатных символов;

R - множество соответствующих конечных отношений.

Для удобства обозначим отношения так же, как и предикатные символы, т.е. I ( PAggrWhole )= PAggrWhole, I ( PPropCharacter )= PPropCharacter, I ( PHierIndex ) = PHierIndex , I ( PHierCategory ) = PHierCategory .

Тогда рабочую память можно представить в виде таблиц, идентификаторы которых будут соответствовать отношениям из множества R (рис. 3).

PAggrWhole(x,y)         PPropCharacter(y,z) PHierlndex(x,k) HierCategory(x,z)

PAggrWhole		PPropCharacter		PHierIndex		HierCategory
Элемент текста-целое	Элемент текста-часть	Элемент текста	Свойства элемента	Элемент текста	Индекс	Элемент текста	Категория

Рис. 3. Интерпретирующее отображение текущей системы продукций

База правил содержит системы продукций, релевантные различным методам автоматической языковой обработки текста на естественном языке. Поэтому отдельная система продукций может иметь свое множество предикатных символов P_k . Однако это множество всегда конечно, что позволяет производить настройку рабочей памяти на систему продукций.

Механизм формирования рабочей памяти

Заполнение таблиц рабочей памяти осуществляется на основе естественно-языковой обработки научного текста по схеме, представленной на рисунке 4.

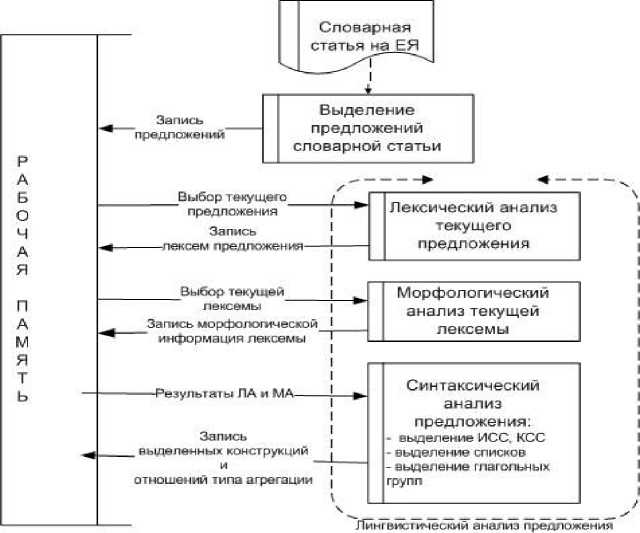
Рис. 4. Схема формирования рабочей памяти

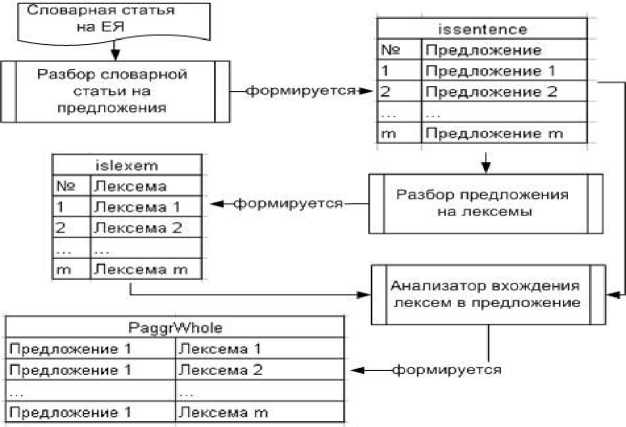
Рис. 5. Схема лексического анализа

Для того чтобы заполнить таблицы рабочей памяти соответствующими фактами, проводится разбор словарной статьи на предложения, затем каждое предложение подвергается анализу, включающему в себя три этапа: лексический анализ, морфологический анализ, синтаксический анализ. Кратко опишем каждый этап.

На первом этапе на вход лексического анализатора подается предложение из словарной статьи, которое разбирается на лексемы. Результатами разбора заполняется таблица PAggrWhole. Как видно из рисунка 5, для формирования таблицы PAggrWhole используются две вспомогательные таблицы issentence и islexem. В таблице issentence хранятся предложения и их индексы в словарной статье. В таблице islexem хранятся лексемы и их индексы в текущем предложении. Вспомогательные таблицы не используются при логическом выводе, они нужны для хранения промежуточных данных и их передачи между процессами.

Следующий этап формирования рабочей памяти заключается в заполнении таблицы PPropCharacter найденной морфологической информацией лексемы. Морфологический анализ заключается в определении части речи лексемы с индексом i. В зависимости от того, к какой части речи относится лексема, определяются соответствующие морфологические ха- рактеристики. В результате работы данного анализатора в таблицу PPropCharacter заносится морфологическая информация текущей лексемы, например, часть речи, род, падеж.

Синтаксический анализ является наиболее сложным. Основной целью синтаксического анализатора в данной работе является выделение таких единиц текста, как устойчивые словосочетания. Выделение словосочетаний осуществляется на основе морфологической информации словоформ и их позиций в предложении. Для этого используются шаблоны, определяющие наиболее распространенные комбинации сочетаний связанных между собой единиц текста [1].

Синтаксический анализатор при своей работе использует таблицы лексем, морфологической информации и шаблоны и формирует таблицу словосочетаний. На этом основании выделенные словосочетания добавляются в таблицу PAggrWhole. Кроме того, заполняется таблица PHierIndex, в которой выделенным лексемам и словосочетаниям присваиваются индексы.

Для экспериментальной апробации схемы, представленной на рисунке 4, был разработан программный прототип, включающий лексический, морфологический и синтаксический анализаторы, а также модуль построения и заполнения рабочей памяти. Кроме того, было реализовано представление рабочей памяти в формате XML и виде таблиц реляционной базы данных. На разработанном программном обеспечении была проведена серия экспериментов по построению рабочей памяти на основе обработки словарных статей терминологического словаря. Эксперименты подтвердили адекватность разработанной модели рабочей памяти и работоспособность подхода к ее формированию. Полученные результаты могут быть использованы при реализации модуля управления продукционными знаниями.

Выводы

Выполненные теоретические изыскания позволили разработать программный прототип, который является компонентом системы автоматической обработки текста на естественном языке и автоматически формирует рабочую память, настраиваясь на заданные продукционные системы. Несмотря на требующиеся дополнительные исследования и доработки, которые были выявлены в процессе тестирования, данная работа имеет практическую значимость для развития исследований, проводимых в области построения интеллектуальных систем, основанных на правилах.