Модель расчёта поглощения энергии от инкорпорированных излучателей моноэнергетических электронов в объектах природной биоты
Бесплатный доступ
Предложена модель, позволяющая рассчитывать поглощение энергии от инкорпорированных излучателей моноэнергетических электронов в организмах различной геометрии. Показана эффективность вычисления поглощённых фракций для организмов сферической, эллипсоидальной и цилиндрической формы путём сравнения расчётных значений с референтными данными. Уравнения модели не содержат подгоночных коэффициентов и не нуждаются в проведении процедур компьютерной интерполяции. Предложенный подход позволяет выполнять корректные экспресс-расчёты доз внутреннего облучения биологических объектов различной формы от бета-излучающих радионуклидов без использования методов компьютерного моделирования Монте-Карло. Модель может быть использована в задачах радиационной дозиметрии биоты и радиационной защите окружающей среды.
Доза, модель, расчёт, уравнения, поглощение энергии, сферы, эллипсоиды, цилиндры, масштабирование, внутреннее облучение, электроны, радиационная безопасность, радионуклиды, защита, окружающая среда
Короткий адрес: https://sciup.org/170179210
IDR: 170179210 | УДК: 539.1.074:574 | DOI: 10.21870/0131-3878-2021-30-2-113-122
Текст научной статьи Модель расчёта поглощения энергии от инкорпорированных излучателей моноэнергетических электронов в объектах природной биоты
Расчёт внутреннего облучения биологических объектов от инкорпорированных радиоактивных веществ является достаточно сложным разделом радиационной дозиметрии. Оценки дозы внутреннего облучения необходимы в радиационной терапии, диагностике с применением радиоизотопов, в задачах радиационной защиты человека и биоты от повреждающего действия ионизирующих излучателей.
В стандартной методике, разработанной Комитетом по медицинской внутренней дозиметрии (MIRD), поглощение энергии внутри заданного биологического объекта может быть выражено в терминах радиационной поглощённой фракции от общей энергии, выделенной в данном объёме [1-3].
Оценка величины поглощённой фракции
является ключевой задачей для внутренней дозиметрии различных биообъектов. Расчёт поглощённой фракции может быть выполнен либо численным интегрированием функции точечного источника по объёму для простой геометрии [2, 3], либо путём компьютерного моделирования с использованием метода Монте-Карло [4-6]. В медицинской дозиметрии опубликованы справочные таблицы поглощённых фракций от инкорпорированных эмиттеров разных энергий в биообъектах, релевантных для медицинских целей [4, 6, 7], данные получены с помощью компьютерных программ Монте-Карло.
В радиационной дозиметрии природной биоты были опубликованы значения поглощённых фракций внутреннего облучения для ограниченного набора биологических сфер с массами от 10-6 до 103 кг (всего 10 размеров с 10-кратным интервалом) и 18 значений энергий электронов [5, 8], расчёты были выполнены с использованием компьютерной системы MCNP4. Для других размеров биообъектов предложена схема интерполяции между имеющимися данными расчёт-
Сазыкина Т.Г.
– гл. науч. сотр., д.ф.-м.н.;
Крышев А.И.*
– зав. лаб., д.б.н. ФГБУ «НПО «Тайфун».
ной сетки с использованием формул, включающих многочисленные подгоночные параметры. Также была предложена методика преобразования расчётов от сфер к эллипсоидам [5, 8]. На основе результатов перечисленных публикаций была создана европейская компьютерная система ERICA Tool, ставшая одним из основных инструментов расчёта доз на биоту в европейских странах и в РФ [9, 10] (см. также интернет-сайт . Та же методология и интерполяционные методы заложены и в более современном электронном дополнении к Публикации 136 МКРЗ, в котором рассчитываются значения дозовых коэффициентов по заданным размерам организма и заданному радионуклиду [11], доступ на интернет-сайте Разнообразные методы интерполяции, применяемые в радиационной дозиметрии биообъектов, содержат большое число подгоночных параметров (от семи и более параметров), которые подгоняются таким образом, чтобы соответствовать в точках расчётной сетки дискретным значениям, полученным из программ Монте-Карло. Разнообразие форм и размеров организмов в природе очень велико, использование при расчёте дозовых нагрузок для каждого типа организмов компьютерных программ Монте-Карло является чрезмерно затратным. В данной работе основная цель состояла в создании метода прямого аналитического расчёта поглощённых фракций без применения компьютерного моделирования методом Монте-Карло, а также без введения многочисленных подгоночных параметров. В следующих разделах метод изложен применительно к биообъектам в виде сфер из мягкой биологической ткани. Излучатель моноэнергетических электронов предполагается равномерно распределённым в биообъекте. Представлена схема адаптации метода для расчёта поглощённых фракций электронного излучения в эллипсоидах. Данные и методы расчёта Выбор независимых международных баз данных значений поглощённых фракций электронного излучения в сферических биообъектах Проверка работоспособности нового методического подхода и аналитической модели должна проводиться на независимых данных достаточно высокого качества, которые могут быть использованы в качестве истинных референтных значений при тестировании модели. С этой целью был выполнен анализ литературы и подобраны обширные зарубежные базы данных значений поглощённых фракций электронного излучения в сферических биообъектах, рекомендованные для использования в медицинской дозиметрии и в дозиметрии природной биоты [4-8].
В имеющихся публикациях наборы значений поглощённых фракций
для биологических сфер представлены в виде обширных таблиц и графиков для различных значений размеров объектов и энергий электронов [4-8]. Графики поглощённых фракций демонстрируют нелинейные зависимости как от радиуса
R
, так и от энергии
E
в виде однотипных гладких кривых, смещённых относительно друг друга для разных
R
и
E
и изменяющихся в диапазоне значений [0, 1]. При рассмотрении серий однотипных графиков
(i(E,R') Универсальная кривая поглощённых фракций в сферах с равномерно распределённым излучателем моноэнергетических электронов Гипотеза о возможности существования универсальной дозовой кривой для электронного излучения была впервые высказана в конце 1960-х годов в работах Д.П. Осанова и Г.Б. Радзиев-ского [12] (см. также описание в книге [13]), которые предположили возможность существования универсальной кривой для изучаемых ими дозовых распределений от широких пучков моноэнер-гетических электронов при использовании масштабирования расстояний на длины пробегов электронов.
Имея в виду гипотезу об универсальной кривой, было необходимо произвести масштабирование размеров биообъектов, выразив их в виде безразмерных эффективных радиусов. Естественным способом получения безразмерного эффективного радиуса
R
eff
было масштабирование (шкалирование) реального радиуса
R
на среднюю длину пробега ионизирующей частицы (электрона) в мягкой биологической ткани. Таким образом, для моноэнергетических электронов
R
β,eff
=R/Λ(E
β
)
, где
Λ(E
β
)
, см – длина пробега электрона с начальной энергией
E
β
в мягкой биологической ткани. Значения
Λ(E
β
)
являются стандартными табличными величинами, они рассчитаны для разных материалов, включая мягкие биологические ткани. Справочные таблицы значений длин пробегов электронов разных энергий имеются в справочниках по радиационной дозиметрии [14].
Применение масштабирования к международным базам значений поглощённых фракций в мягкотканных сферах выявило существование единой универсальной кривой поглощённых фракций как функции одного аргумента – безразмерного эффективного радиуса биообъекта, как подробно описано в нашей статье [15]. Фрагмент универсальной кривой поглощённых фракций электронов с указанием референтных данных показан на рис. 1.
Рис. 1.
Фрагмент универсальной кривой поглощённых фракций электронного излучения в мягкотканных сферах (модифицировано из публикации [15]).
Отметим, что в работе [16] кривая сходного вида была получена путём аппроксимации собственных расчётов по программе Монте-Карло поглощения энергии электронов в сферических объектах для целей медицинской дозиметрии. В качестве базы для масштабирования в работе
[16] было предложено расстояние (X
99
), на котором поглощается 99% энергии моноэнергетиче-ских электронов, испущенных из центра сферы; аппроксимация как величин X
99
, так и результирующей кривой для поглощённых фракций была выполнена с использованием ряда параметров.
Модель расчёта определения поглощённых фракций энергии от инкорпорированных излучателей моноэнергетических электронов в сферических биообъектах
В соответствии со специфической формой универсальной кривой новая расчётная формула для
ф
в
(R
в
,
eff
)
должна иметь следующие свойства:
• функция одного аргумента
R
e
,
eff
;
• гладкая кривая, изменяющаяся в пределах 0-1;
• функция с насыщением по величине
R
e
,
eff
.
Простейшей математической формулой кривой с насыщением, удовлетворяющей перечисленным выше свойствам, является зависимость типа формулы Моно. В нашей работе [15] было показано, что уравнения для расчёта поглощённой фракции для моноэнергетических электронов и сферических биообъектов имеют вид:
фР (R P.ef f
)
= t|
0,5
;
R р,е f f
=
XT^
;
(1)
RP^ff
®
P(RP^ff
)
= exp(1 —
Rp,eff
),
если
Rp^ff
< 1;
RP(RP,eff
)
=
1
,
если
R p,e f f
^ 1 ;
где
ф
в
(R
в,eff
)
- поглощённая фракция электронного излучения в сфере радиуса
R
, см;
R
в
,eff
=R/Л(E
в
)
- масштабированный эффективный радиус сферы (безразмерный);
Л(Е
в
)
- пробег электрона в мягкой биологической ткани, см;
0
e
(R
e
,e«
)
- корректирующая аналитическая функция, отличная от 1 при
R
e
,eff
<1.
Выражение (1) для расчёта поглощённых фракций электронов в сферах является функцией одного безразмерного аргумента
R
e
,eff
, который содержит одновременно информацию о размере биообъекта и энергии электронов. С помощью (1) поглощённые фракции могут быть рассчитаны непосредственно без подгоночных параметров и без применения методов Монте-Карло.
Модификация модели для расчёта поглощённых фракций электронного излучения в биообъектах несферической формы
Для расчёта поглощённых фракций ионизирующих излучений в мягкотканных эллипсоидах Э. Амато (E. Amato) с соавторами [6, 7] была разработана оригинальная методика, в которой продемонстрировано, что поглощённые фракции энергии внутреннего излучения одинаковы для эллипсоида и сферы, имеющей такое же отношение «объём/поверхность» как у исходного эллипсоида. В указанной методике при расчёте поглощённых фракций эллипсоид с объёмом
V
и площадью поверхности
S
аппроксимируется суррогатной сферой с генерализированным радиусом
R
cypp
, который для эллипсоида рассчитывается по формулам:
R^p = 3
-
,V =
4
m-a-b-c;
(2)
5 = 4я [(a:b)^+a.£)^+b:£^]d; d = 1пЗ/1п2 ^ 8/5, где а, b, c - полуоси эллипсоида; V, S - объём и площадь эллипсоида. Таким образом, применительно к эллипсоидным биообъектам задача преобразуется к определению поглощённой фракции электронного излучения в суррогатной сфере с помощью уравнений (1). В дозиметрии природной биоты применение метода Амато оказывается весьма полезным, поскольку большинство животных при расчётах доз аппроксимируются однородными эллипсоидами разных размеров. В дозиметрии биоты [6-8, 11, 17] для случаев непрерывного энергетического спектра бета-излучения радионуклида обычно производится аппроксимация спектра дискретным значением, равным средней энергии бета-излучения. При необходимости более точного расчёта может быть произведена более детальная аппроксимация непрерывного бета-спектра [18]. Примеры практического применения метода для аналитических расчётов дозовых коэффициентов внутреннего облучения эллипсоидных организмов биоты от инкорпорированных бета-излучающих радионуклидов приведены в нашей статье [15], также дозовые коэффициенты приводятся в работах [5, 11, 19].
Представляет интерес дальнейшее расширение применимости нового метода для расчёта поглощённых фракций электронного излучения в телах цилиндрической формы. Так же, как сфера и эллипсоид, цилиндр является выпуклым телом и для него величина средней хорды пропорциональна отношению «объём тела/площадь», т.е. V/S. Аналогично формуле (2) для эллипсоидов, радиус суррогатной сферы для цилиндра радиусом
r
и высотой
h
рассчитывается по формулам:
R^ = 3^, V нт2К
(3)
5ц = 2тг • г • (г +
К).
Результаты и обсуждение Тестирование аналитических результатов на независимых международных данных значений поглощённых фракций моноэнергетических электронов
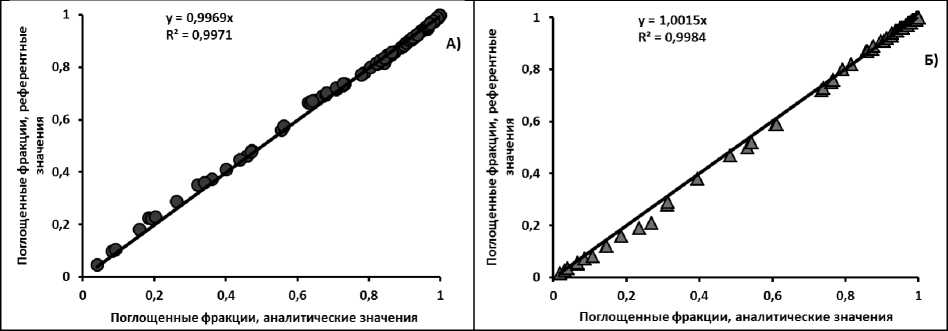
Аналитические значения поглощённых фракций были рассчитаны для геометрических моделей разных размеров и форм. Аналитические значения сравнивали с рекомендованными из медицинской дозиметрии, опубликованными в работе [4] и с данными по дозиметрии биоты [5]. На рис. 2 представлены корреляции между аналитическими значениями для сферических биообъектов и референтными значениями поглощённых фракций электронов, взятых из публикаций разных авторов: рис. 2А показывает корреляцию с данными Стабина и Конейненберга [4] (расчёты Монте-Карло по программе MCNP); рис. 2Б - корреляцию между аналитическими значениями и данными Улановского [5] для сферических биообъектов. Сравнивались значения поглощённых фракций для одинаковых значений энергии электронов и одинаковых размеров сфер. Корреляционный анализ подтверждает хорошее согласие аналитического расчёта с независимыми международными данными, соотношение аналитических данных с расчётными описывается линейной зависимостью
Y=kX
, где величина
к
составляет значения 0,99-1, коэффициенты корреляции выше 99%.
Рис. 2.
Корреляции между аналитическими значениями поглощённых фракций электронного излучения (сферические тела) и международными референтными данными [4, 5].
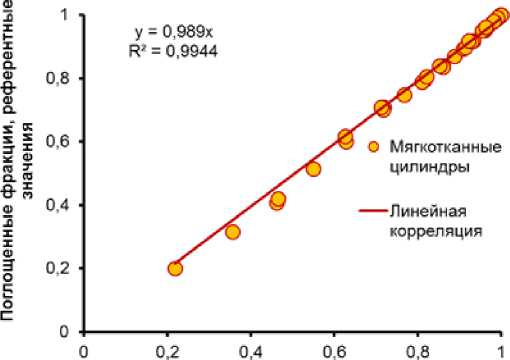
A – Сравнение с данными публикации [4]; Б – сравнение с референтными данными из публикации [5]. На рис. 3 представлены корреляции между аналитическими значениями поглощённых фракций электронов, рассчитанными по формулам (1)-(3) для мягкотканных цилиндров и независимыми референтными значениями, полученными в публикации [20] с помощью современной компьютерной программы Монте-Карло GEANT4. Сравнение показывает хорошую применимость аналитического метода для объектов цилиндрической формы. Поглощенные фракции, аналитические значения
Рис. 3.
Корреляции между аналитическими значениями поглощённых фракций электронного излучения (мягкотканные цилиндры) и референтными данными из публикации [20].
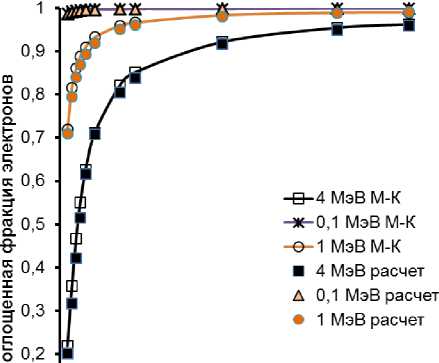
На рис. 4 представлено более детальное сопоставление величин поглощённых фракций электронов для разных объёмов цилиндров (от 1 до 105 см3, h=1,5r) для нескольких значений энергий электронов – 0,1; 1 и 4 МэВ; тестовые данные взяты из публикации [20], аналитические значения рассчитаны с помощью формул (1), (3). Как видно из представленных данных, новый метод имеет хорошую работоспособность для выпуклых биологических тел, включая сферы, эллипсоиды и цилиндры, что позволяет рассчитывать поглощённые фракции электронов для большинства объектов животного мира. с 0.1 ■ о --------------------.--------------------.--------------------.--------------------.--------------------. О 2 4 6 8 10 Отношение "объем/площадь" цилиндра
Рис. 4.
Аналитические значения поглощённых фракций электронов в телах цилиндрической формы в зависимости от соотношения объёма и площади; сравнение с референтными данными из публикации [20].
Заключение Разработана модель расчёта поглощения энергии от источников моноэнергетических электронов, равномерно распределённых в животных объектах природной биоты разной формы. Модель включает масштабирование реальных размеров организмов на стандартные средние длины пробегов электронов. Предложенные уравнения расчёта не связаны с компьютерными методами Монте-Карло, а также не содержат подгоночных параметров и не требуют интерполяций между расчётными точками. Показана работоспособность уравнений для расчёта поглощения моноэнергетических электронов не только в сферах, но и в эллипсоидах и цилиндрах. Модель предоставляет возможность простого и общедоступного экспресс-расчёта поглощённых фракций бета-излучающих радионуклидов и дозовых нагрузок для различных объектов природной среды. Подход может иметь широкое применение в задачах оценок радиационной безопасности живых организмов, а также в задачах радиационной защиты окружающей среды.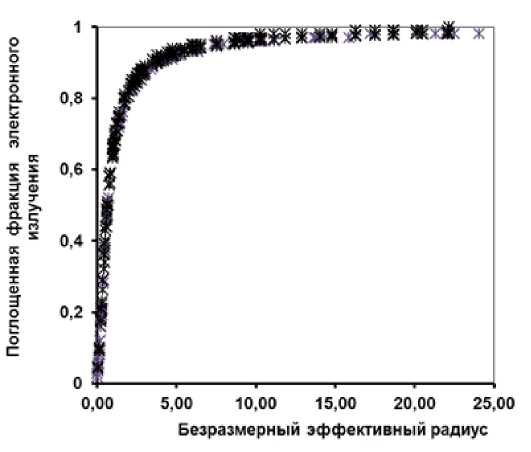
Список литературы Модель расчёта поглощения энергии от инкорпорированных излучателей моноэнергетических электронов в объектах природной биоты
- Loevinger R., Berman M. A revised schema for calculating the absorbed dose from biologically distributed radionuclides. MIRD Pamphlet N 1, revised. New York: Society of Nuclear Medicine, 1976. P. 3-10.
- Хайн Дж., Браунелл Г. Радиационная дозиметрия: пер. с англ. /под ред. Н.Г. Гусева, К.А. Труханова. М.: Издательство иностранной литературы, 1958. 758 с.
- Руководство по радиационной защите для инженеров. Т. 2: пер. с англ. /под ред. Д.Л. Бродера. М.: Атомиздат, 1973. 288 с.
- Stabin M.G., Konijnenberg M.W. Re-evaluation of absorbed fractions for photons and electrons in spheres of various sizes //J. Nucl. Med. 2000. V. 41, N 1. P. 149-160.
- Ulanovsky A., Prohl G. A practical method for assessment of dose conversion coefficients for aquatic biota //Radiat. Environ. Biophys. 2006. V. 45, N 3. P. 203-214.
- Amato E., Lizio D., Baldari S. Absorbed fractions in ellipsoidal volumes for p" radionuclides employed in internal radiotherapy //Phys. Med. Biol. 2009. V. 54, N 13. P. 4171-4180.
- Amato E., Lizio D., Baldari S. Absorbed fractions for electrons in ellipsoidal volumes //Phys. Med. Biol. 2011. V. 56, N 2. P. 357-365.
- Ulanovsky A., Prohl G., Gomez-Ros J.M. Methods for calculating dose conversion coefficients for terrestrial and aquatic biota //J. Environ. Radioact. 2008. V. 99, N 9. P. 1440-1448.
- Brown J.E., Alfonso B., Avila R., Beresford N.A., Copplestone D., Hosseini A. A new version of the ERICA Tool to facilitate impact assessments of radioactivity on wild plants and animals //J. Environ. Radioact. 2016. V. 153. P. 141-148.
- Brown J.E., Alfonso B., Avila R., Beresford N.A., Copplestone D., Prohl G., Ulanovsky A. The ERICA Tool //J. Environ. Radioact. 2008. V. 99, N 9. P. 1371-1383.
- ICRP, 2017. Dose coefficients for non-human biota environmentally exposed to radiation. ICRP Publication 136 //Ann. ICRP. 2017. V. 46, N 2. P. 1-136.
- Osanov D.P., Tissen M.U., Radzievsky G.B. Dose distribution of p-radiation of fission products in the tissue equivalent material //Health Phys. 1969. V. 17, N 3. P. 484-495.
- Осанов Д.П. Дозиметрия и радиационная биофизика кожи. M.: Энергоатомиздат, 1990. 233 с.
- Машкович В.П., Кудрявцева А.В. Защита от ионизирующих излучений. М.: Энергоатомиздат, 1995. 494 с.
- Sazykina T.G., Kryshev A.I. A new analytical method for estimating electron-absorbed fractions in soft-tissue biological volumes //Radiat. Environ. Biophys. 2021. V. 60, N 1. P. 141-149.
- Степаненко В.Ф., Яськова Е.К., Белуха И.Г., Петриев В.М., Скворцов В.Г., Колыженков Т.В., Петухов А.Д., Дубов Д.В. Расчёты доз внутреннего облучения нано-, микро- и макро-биоструктур электронами, бета-частицами и квантовым излучением различной энергии при разработках и исследованиях новых РФП в ядерной медицине //Радиация и риск. 2015. Т. 24, № 1. С. 35-57.
- ICRP, 2008. Environmental protection - the concept and use of reference animals and plants. ICRP Publication 108 //Ann. ICRP. 2008. V. 38, N 4-6. P. 1-242.
- ICRP, 2008. Nuclear decay data for dosimetric calculations. ICRP Publication 107 //Ann. ICRP. 2008. V. 38, N 3. P. 1-96.
- Amato E., Italiano A. An analytical model for calculating internal dose conversion coefficients for non-human biota //Radiat. Environ. Biophys. 2014. V. 53, N 2. P. 455-459.
- Rahman Z., Rehman S.U., Mirza S.M., Arshed W., Mirza N.M. Geant4-based comprehensive study of the absorbed fraction for electrons and gamma-photons using various geometrical models and biological tissues //Nucl. Technol. Radiat. Prot. 2013. V. 28, N 4. P. 341-351.


