Модель распространения радиоволн в диапазоне частот 1-10 МГц на основе метода нормальных волн

При анализе декаметровых радиотрасс метод нормальных волн [Куркин и др., 1981] оказывается достаточно эффективным, что было неоднократно продемонстрировано с использованием разработанного программного комплекса [Алтынцева и др., 1987]. В рамках метода нормальных волн электромагнитное поле излучения внутри волновода Земля– ионосфера представляется в виде ряда, вообще говоря бесконечного, по собственным функциям радиального оператора. При этом для численных расчетов ряд ограничивается так называемой группой слабозатухающих волн. Несущая частота сигнала при таком способе расчета спектра должна быть больше минимальной критической частоты на трассе распространения, тогда в каждой точке волновода существует номер нормальной волны, с которого поле перестает отражаться от ионосферы. В случае если частота меньше критических частот по трассе, группа слабо просачивающихся волн становится бесконечной. При этом реальные части спектрального параметра образуют последовательность, сходящуюся к нулю, что физически соответствует наличию углов распространения, сколь угодно близких к вертикали. Мнимые части спектрального параметра растут с номерами, но обусловлено это не прохождением волн через ионосферный барьер, а поглощением в ионосфере. В этом случае ранее применявшийся алгоритм неприменим. В работе приведена модификация метода нормальных волн для решения радиальной задачи и построения спектра радиального оператора. Разработан численный алгоритм расчета поля для рабочих частот низкочастотной части декаметрового и средневолнового диапазона, для которых существует регулярный волновод Земля–ионосфера и число нормальных волн достаточно велико.

Постановка задачи

Рассматривается азимутально-симметричный неоднородный сферический волновод Земля–ионосфера.

Для выбранной модели волновода фурье-компоненты электромагнитного поля в точке приема ( r, 0 ) имеют вид [Куркин, Хахинов, 1984; Попов, Потехин, 1984]:

E 'I ф

n

—

X

A ar Vsin 0

= De ( Ф ) x

a— Y n ( 0 ) R e ( r , 0 )

1      d (Ve( r , 0 ) R n ( r , 0 ))

ik 8 ( r , 0 )           d r

V e ( r , 0 ) R e ( r , 0 )

ih J y n ( 0' ) d 0- e ⁰          ,

B r

B 0 | E ф

X

Здесь

I=— i  A^ ^ ^= Dm ( ф ) x

arWnO n v^ ,0,

- Y m ( 0 ) R m ( r , 0 ) r

£ d R m ( r , 0 )

k    dr

ih J y m ( 0' ) d 0' e ⁰

R m ( r , 0 )

4 2 n k-³ i n

c

h = ka , a – радиус Земли.

R e ^, m ( r , 0 ) и Y e ^, m =Y e ^, m + i v e ^{, m} - собственные функции и собственные значения соответствующих радиальных краевых задач для магнитного ТМ (со значком « е ») и электрического ТЕ (со значком « m ») полей [Куркин и др., 1981]. Эффективность возбуждения нормальных волн характеризуется величинами

D e ( ф ) и D m ( ф ) соответственно. Логично назвать их коэффициентами возбуждения нормальных волн. Коэффициенты возбуждения нормальных волн

D e ^, m ( ф ) являются интегралами по объему V 1 ( r 1 , O 1 ,

ф 1 ), занятому источником поля, и представляют собой аналоги диаграмм направленности излучающих антенн [Куркин, Хахинов, 1984]:

D e ( ф ) -л

r д ( R (Г 1 )) _х

ДГ)     ⁸ Г

X [ ^j _O СО8⁽ ф ^- ф 1 ) + ^j ф 81П⁽ ф ^- ф 1 ) ] + jr ^у R ⁽ r i ) } х exp⁽ - ih у * O i с^о8⁽ ф-ф 1 )⁾

^х      r?re     ad"^1,

D m ⁽ ф ) ^- J [ ^j ф ^со8( ф ^- ф 1 ) ^{- j} _O ⁸ⁱⁿ⁽ Ф ^- ф 1 ) ] ^X

х ^n ⁽ r i ) exp ( - ih у m Oj со8( ф - ф] ) ) d" . r i            '                                '

Таким образом, поле внутри волновода Земля– ионосфера в рамках волноводного подхода представляется в виде ряда по собственным функциям радиальной краевой задачи с импедансными условиями на поверхности Земли и условиями излучения на бесконечности [Куркин и др., 1981]. Радиальное уравнение имеет вид d 2R

+ hQ ( y , г- i x ) R - 0,                      (5)

dy

где

E + ix

Q ^{- 1 -}a q_x⁽y ) + i p q ₂ ⁽ y )--—^,

У

^ + i x-у ² - ( у + i v )², у = rI a , a-® 0 / « ,

p ^{- av} e_fr / ® ²' q 1 ⁽ y ) ^- q ⁽ y ^), q 2 ⁽ y ) ^- q ⁽ y ) ^{q (} y ) q ( y ) ^-профиль электронной концентрации N(у ), нормированный на единицу в точке максимума, q ( y ) - профиль эффективной частоты соударений с нейтралами v _eff, нормированный на единицу в точке начала ионосферы. Здесь и далее у собственных функций и собственных значений подразумевается наличие индекса n . Граничное условие для радиальной функции на поверхности Земли

-R + ^ihS s t ^-^^- i x ^R

- 0,

где S =1 для магнитного диполя, S =1I s _t для электрического диполя, s _t - комплексная диэлектрическая проницаемость земной поверхности. Условие излучения на бесконечности

z₂ - у ₂ + i ф₂ функции Q ( z , ^ + i x ) определяют точки отражения (поворота). В зависимости от значения спектрального параметра нижней точкой отражения является поверхность Земли или точка Z i - V^ + i x - У + i v . В окрестности верхней точки отражения z ₂ меняет знак Re Q ( z , ^ + i x ), поэтому из условия Re Q ( z , ^ + i x ) - 0 можно приближенно записать выражение для вещественной части ^ - у ² - v ² :

у ² -v ² - y ²[1 -a ² q 1 ( y )].                        (8)

В реализованном ранее комплексном алгоритме моделирования декаметрового радиоканала на основе метода нормальных волн [Куркин и др., 1981; Ал-тынцева и др., 1987] предполагалось, что рабочая частота больше минимальной критической частоты Р2-слоя на радиотрассе. Данное предположение соответствует условию существования идеального волновода Земля–ионосфера. Коэффициент в радиальном уравнении (5) для такого волновода больше нуля, Q ( y , у ) >  0, вне точек поворота Q ( y , у ) - 0. При учете мнимой части спектрального параметра v ограничение снизу на рабочую частоту по критической частоте слоя F2 снимается, так как решение уравнения (8) для таких частот существует.

Собственные значения у ² - ^ + i x радиальной задачи (5)-(7) в комплексной плоскости ( ^ , x ) расположены в верхней полуплоскости, так как ^ = у ²- v ², x =2 уv . В комплексной же плоскости ( у , v ) значения спектрального параметра у + i v - ^^ + i x расположены в верхнем правом квадранте. В области рабочих частот, меньших критической частоты слоя F2, вещественная часть спектрального параметра у стремится к нулю, а мнимая часть v резко возрастает. При этом для определенной части спектра собственных значений для рабочих частот низкочастотной части декаметрового и средневолнового диапазонов существует регулярный волновод Земля–ионосфера и число нормальных волн достаточно велико. Таким образом, в предлагаемой модели распространения радиоволн ограничение на рабочую частоту по критической частоте слоя F2 снимается и вклад мнимой части собственного значения в характеристики нормальных волн учитывается по квадрату спектрального параметра радиальной задачи.

Решение радиального уравнения

Решение уравнения (5) вне окрестностей точек поворота z 1 , z ₂ записывается в виде ВКБ-приближения [Хединг, 1965]:

„  C ±

R - — exp

4 Q

z

f dR lim | — - ihR I- 0.

у ^^ у dy     у

Вещественную независимую переменную у в коэффициенте уравнения (5) можно заменить комплексной переменной z . Нули z_x - y_T + i ф_г и

где C - произвольные константы. В области точек поворота z 1 , z ₂ решение уравнения (5) строится с использованием эталонного уравнения Эйри [Хединг, 1965; Куркин и др., 1981].

Построим решение радиальной краевой задачи вблизи поверхности Земли в окрестности точки

z_x = Y = Y + i v . Так как в этой области у = 1, то | Y| = 1. Функцию Q ( z , I + i х ) при |Y| = 1 в окрестности z_x = Y приближенно можно представить в виде линейной функции:

Q ( z , I + i X ) = 2( z -Y ). Y

Тогда решение радиальной задачи вблизи поверхности Земли находится по схеме, приведенной в [Куркин и др., 1981]. В уравнении (5) сделаем замену

описывают распространение электромагнитного поля в наземном волноводе, а волны, отвечающие значениям y >1, - в надземном волноводе [Куркин и др., 1981].

Удобно ввести параметр А = 2(2/ h )^2/3, который соответствует |Re x ( y± А )| « 4. Тогда при y <1-A имеется одна точка отражения в ионосфере и ВКБ-реше-ние (18) можно продолжить до поверхности Земли:

у = у ( x ), R ( у ) =

PZZ ( x ) dx

и приведем его к эталонному уравнению Эйри:

Подставив (19) в граничное условие (6), найдем значение фазы Ф, пренебрегая малыми слагаемыми:

Z"-xZ = 0,                                (12)

где

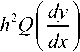
i in YIziz / x^ S YI l zAz i x

²   V V^{1 -I}- i X - ^s4 ¹ 1 ^{- I}- i X₎

Граничное условие (6) примет вид

Z ' + ihS [ — Ъе t -I- i х Z

V dx )

= 0,

где x i - значение x ( y ) при y =1.

Решение уравнения (12) с граничным условием (13) записывается в виде линейной комбинации функций Эйри и ( х ) и и ( х ):

Когда 1 -A, решение (5) определяется выражением (14) и внутри волновода переходит в ВКБ-решение (18) с точкой поворота z 1=1 (y< 1) и z_x = Y (Y>1). При y>1+A можно воспользоваться асимптотикой функций Эйри в выражениях (15) и (16). Тогда

Ф =

п

4,

R ( x ) = С _н/- h — х dx

R ( x ) = C j - h^- и ( x )

х [ u ( x) sin( ц - Ф ) + u ( x ) cos( ц - Ф ) ] .

и решение уравнения (5) в волноводе имеет вид

2 Z     X     . П                      П          . 1

Здесь ц = — ( - x )  + — при y <1, ц = — при y >1,

Ф = arctg

A cos ц + B sin ц | B cos ц- A sin ц ) ’

_C       у      _п

^R = tA^{cos h} { ^Qdy - ^--V ^Y                 .

где

A =

u '( x ) + ihS |    | J | -1 - i x u ( x )

V dx ) ⁴

B = u‘ ( x ) + ihS

С 1 - константа.

Выражение х(у ) можно записать в виде

x = -

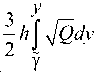
2/3

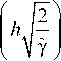
^{( y-} у ^).

С использованием асимптотик функций Эйри и ( х ) и и ( х ) при - Re x >>  1 решение (14) может быть преобразовано к виду, совпадающему с ВКБ-решением уравнения (5):

R =

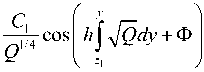
В формуле (18) z 1 =1 при y <1 и z = Y при y >1.

Нормальные волны, отвечающие значениям y <1,

Для точки поворота в ионосфере решение (5) ищем, используя эталонное уравнение Эйри и выбирая только убывающее решение «в глубь ионосферы» [Куркин и др., 1981]. Оно имеет следующий вид:

R(О = C ₂ /- hd^ o ( _S ).

V    d д

Асимптотика решения в волноводе -Reg ^ 1

имеет вид

_C          ^z 2              ]

^R = ^1T4 ^sin ^ h J ^Q2^y y +-

Из условия совпадения решений (18) и (24) внутри волновода получаем уравнение на спектр собственных значений радиальной задачи и связь между константами C 1 и C ₂:

z ₂

h J 4Q ( у + i V , I + i х , в ) dz + Ф ( 1 + i х ) = - + п п , (25)

z ₁

( - 1) " C , = C 2 .

Решение уравнения на спектр

В окрестности точек отражения можно считать, что

Q ( z ) « Q ‘ ( z ^ ₂)( z - z_{v 2}). Тогда, если учесть, что для

нижней точки отражения Q ' ( z_x ) = 2 / z_x , интеграл в окрестности нижней точки поворота можно записать как

J Qdd z - 2 Qz) х

У 1 + i ' 1

3 ^х ( Z - z j²

y = 3 i--¹'^-

Для верхней точки отражения получим выражение z2              2

J Qddz --^4- Qz (z2) X

^{X (} z 2 ^- z ⁾²

2                   3

У 2 = з -Qq^ ( i ' 2 )²-

Так как y «v , то при малом значении v можно пренебречь вкладом мнимых частей точек отражения. Разложим Q и Φ по малым величинам в ^ 2 ( У ) и X , пренебрегая малыми величинами второго порядка:

V Q ( у , ' + ix , в ) - V Q ( у , ' ) -

_      i х       , i ^e q 2 ⁽ у )                             ⁽²⁹⁾

2 у ² У О Т У ) 2 4Qy ’

Ф ( '+ i X ) -Ф ( ' ) + i Ф ' Х -

Отсюда получим уравнения на реальную и мнимую части спектра:

h J V Q ⁽ У , ' ) dy + ^{Re Ф (} У ) ^- Im ^Ф ' ( У х = П + л и ,

У 1

У 2

h J

У 1

^ i p q 2 ⁽ у )  _       i х

. 2 V QУ , ' )  2 У ² V Q ( У , ' )

dy +

+ Im Ф ( У ) + Re Ф ' ( ' ) х = 0.

В первом уравнении мнимой частью производной фазы можно пренебречь по сравнению с интегралом. В итоге получим

У 2

h J 4Q(у, ')dy + Re Ф(') = ^ + лn,(31)

У 1

h [ — ^p q ^{2 ( У} ) dy + Im Ф ( ' )

Х = J^------.(32)

У у ’      . d - Re ^Ф '

Значение константы С ₁ находится из условия биортогональности радиальных функций и равно [Куркин и др., 1981]

У21

С =  [-----,dy

IУ1 2 У2 4 Q (У,')

Модель распространения радиоволн

Для квазимонохроматических сигналов с несущей частотой го выражение для компоненты электриче ского поля Еф (r, t)  в азимутально-симметричном волноводе можно записать в виде nm

E^ (r, t) = Re £ [Bn (r )gо (t - тn)evn(r) Je"iюt,(34)

n = П 1

где  g 0 ( t ) – огибающая излученного импульса,

9r d0'       _ o _ oo OO

Tn (r) = J —^J — задержка нормальной волны на за данную дальность 9, иn - групповая скорость распро-

A странения волны по 9, Bn (r ) = -i-----. ,   (уп )

a ² y Vsin 9

хDm (ф)Rm (r ) - амплитудный множитель нормаль- ной волны, ^и (r ) = hJ (уm + ivm )d9' - фаза волны. o

Пределы суммирования в (34) выбираются из условия эффективного возбуждения ( n ₁) и слабого просачивания сквозь ионосферу ( n_m ) нормальных волн [Куркин и др., 1981].

Поле отдельной нормальной волны распределено по всему сечению волновода и зависит от его глобальных характеристик, суммарное же поле локализовано вблизи траектории луча, где выполнено условие фазировки отдельных групп волн (условие стационарности [Потехин, Орлов, 1981]):

AT n ( r ) = ^-( T n -T n + 1 ) = l , 2 л

где l – целое число. Угол выхода траектории Δ из точки излучения связан с центральным номером n i группы сфазированных нормальных волн соотношением cos А = у_п / y_b л/s. Тогда l - число отражений траектории сигнала от ионосферы.

Приведенные выше выражения служат основой расчета распределения поля декаметрового сигнала в волноводе методом нормальных волн. На первом этапе рассчитываются характеристики нормальных волн B n , Ψ n , τ n , ΔΨ n в опорных точках спектра (31). Количество эффективно возбуждаемых и слабозатухающих нормальных волн составляет порядка 10³–10⁴. Граничные значения группы номеров определяются предельными значениями ' = Re у ². Экстремумы функции в правой части равенства (8) дают ξ_min и ξ_max для частот выше критической частоты. Для частот ниже критической в области, где v ^ y, ^ - - v ². Численные оценки решения уравнения (8) дают значение ξ min ~–10^–3. В реализованном алгоритме расчета характеристик нормальных волн максимальное значение ξ ограничивается высотой начала ионосферы.

На втором этапе решение уравнения (35) относительно номера n позволяет определить модовую структуру сигнала (количество сигналов и их идентификацию) и рассчитать временные и угловые характеристики сигналов. Амплитудные характеристики сигналов вычисляются с использованием формулы (34) по схеме, изложенной в работе [Куркин и др., 1986]. Огибающая сигнала Еф (r, t) = B(r, t)eT(r’ t) вычисляется на основе прямого численного суммирования выражений вида

B ( r ■ t ) =

/\ n=nm

E B n ⁽ r ) g 0 ⁽ t -T n ⁽ r ⁾⁾COS T n ( r )

Vn=n1

~1/2

( n=nm)

⁺ E B n ⁽ r ) g 0 ⁽ t -^T n ⁽ r ^{))sin T} n ⁽ r )

V n=ni

•

Расчет огибающей B ( r , t ) в точке приема позволяет исследовать форму принимаемого сигнала как для разделенных во времени импульсов, так и для перекрывающихся.

Численное моделирование

Комплексный алгоритм расчета характеристик сигналов в рамках предложенной модели распространения базируется на вычислении характеристик нормальных волн B_n , Ψ _n , τ _n , ΔΨ _n в опорных точках спектра. По заданным из модели ионосферы профилям электронной концентрации N ( y ) и эффективной частоты соударений v _eff( y ) рассчитываются значения интегралов

У22                      y2^

1       dy ■  1у\о<у:^> • yf■    dy     ,    ?veffN(y).

dy ■      /dy

¹ 4Q ( y ■ ^ )      y i V Q c y TI)

Спектр эффективно возбуждаемых излучателем и слабозатухающих нормальных волн у 2 = ^_и + iх_п находится из решения трансцендентного уравнения (31) и уравнения (32). Вещественная y n и мнимая v _n части спектрального параметра у_й определяются из системы уравнений

^ n =Y2 -v 2 ■

Xn = 2Ynvn •

На рис. 1 приведены результаты расчета вещественной части γ n спектрального параметра радиальной задачи в зависимости от номера n для рабочих частот 4 и 10 МГц. Здесь и далее тестовые расчеты характеристик нормальных волн проведены для однослойного квазипараболического профиля электронной концентрации с высотой максимума F-слоя 300 км и критической частотой слоя f ₀=6 МГц [Куркин и др., 1981]. При уменьшении рабочей частоты значение γ _n уменьшается и приближается к нулю. Ниже на рис. 2 приведены графики зависимости мнимой части спектрального параметра v _n от значения γ _n для тех же рабочих частот 4 и 10 МГц. Расчеты v _n проводились для электрических параметров «средневлажной» земли с использованием экспоненциального закона изменения эффективной частоты соударений [Куркин и др., 1981]. Линия 1 на рис. 2, б соответствует волнам ТМ-типа, линия 2 – ТЕ-типа. Мнимые части v _n для частоты f =4 МГц резко увеличиваются в ~10² при уменьшении γ _n вблизи нуля, что обусловлено поглощением нормальных волн в ионосфере. На рис. 3 приведены результаты

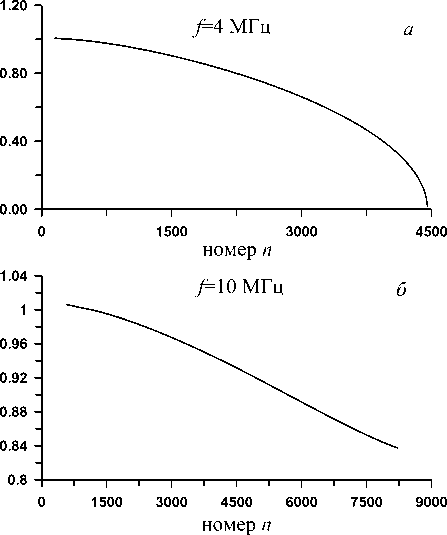
Рис. 1. Зависимости вещественной части спектрального параметра γn от номера n.

0.005

0.004

f =4 МГц

0.003

>       -

0.002

I------------------------------------------1------------------------------------------1------------------------------------------1------------------------------------------1------------------------------------------1------------------------------------------1

0                  0.4                 0.8                 1.2

γ

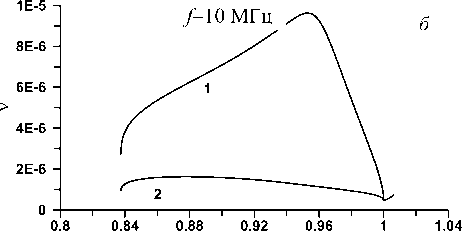
γ

Рис. 2. Зависимость мнимой части спектрального па- раметра vn от уn.

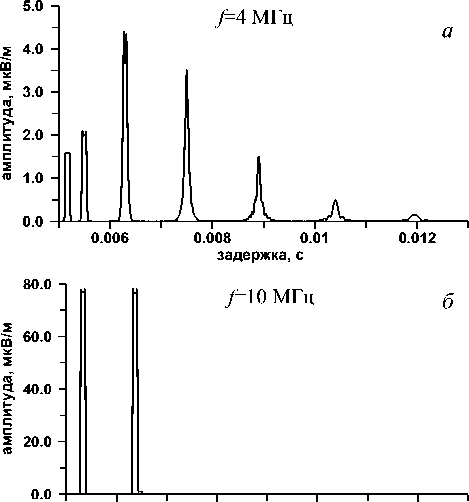
расчетов временной развертки сигнала B ( r , t ) на основе численного суммирования ряда нормальных волн для рабочих частот 4 и 10 МГц на удалении 1300 км от излучателя. На временных развертках сигнала присутствуют отдельные сигналы, разнесенные по времени, которые формируются группами нормальных волн. Значения центральных номеров этих групп можно определить, решая уравнение (35) относительно n , т. е. определяя центральные волны в пакетах сфазированных нормальных волн с номерами n_i . На рис. 4 приведены графики зависимости разности фаз нормальных волн ΔΨ _n от номера n . Штриховыми линиями отмечены центральные номера

0.006

0.008

0.01

0.012

задержка, с

Рис. 3. Временная развертка сигнала, D =1300 км.

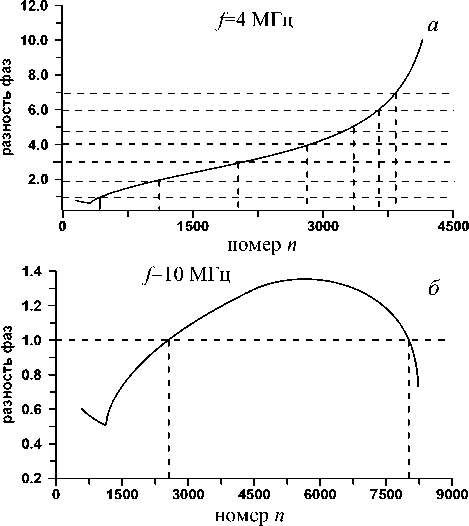
Рис. 4. Зависимость разности фаз ΔΨ _n от номера n .

групп сфазированных нормальных волн, соответствующие решениям уравнения (35) для различных l. Для рабочей частоты f=4 МГц в наземном волноводе (γ<1) для каждого l существует только одно решение уравнения (35) и сигнал в точку приема приходит по траектории с l отражениями от ионосферы. Для частоты f=10 МГц на временной развертке сигнала присутствуют два сигнала, соответствующие нижнему и верхнему лучам односкачкового мода распространения [Куркин и др., 1986]. Таким образом, в отличие от случая f>f0, для частот, меньших критической частоты слоя F2 (f0=6 МГц), сигнал в точку приема может приходить только по одной траектории соответствующего мода распространения. Данная закономерность связана с функциональной зависимостью спектрального параметра от номера волны n (см. рис. 1), которая определяется формой профиля электронной концентрации. Для f>f0 на графике функции γ(n) имеется точка перегиба, в которой ∂2γ

= 0. В геометрическом приближении данное ∂ n ²

условие соответствует условию фокусировки сигнала – верхний и нижний лучи «сливаются» [Куркин и др., 1986]. При f₀ точки поворота решения радиального уравнения (5) в ионосфере могут находиться ниже точки перегиба в высотном профиле электронной концентрации, поэтому функция γ(n) точки перегиба не имеет. Вычисленные задержки центральных волн практически совпадают с задержками переднего фронта отдельных сигналов на временной развертке.

Заключение

В работе в рамках волноводного подхода предложена модель распространения радиоволн в волноводе Земля–ионосфера для низкочастотной части декаметрового диапазона, когда несущая частота сигнала может быть меньше минимальной критической частоты ионосферного слоя вдоль трассы распространения. На основе метода нормальных волн была модифицирована схема решения радиальной задачи и построения спектра радиального оператора. Для частот, меньших критической частоты слоя F2, реальные части спектрального параметра образуют последовательность, сходящуюся к нулю, что физически соответствует наличию углов распространения, сколь угодно близких к вертикали. Мнимые части спектрального параметра растут с номерами, но обусловлено это не прохождением волн через ионосферный барьер, а поглощением в ионосфере. Разработан численный алгоритм расчета электромагнитного поля излучения для частот, для которых существует регулярный волновод Земля–ионосфера и число нормальных волн достаточно велико.

Работа выполнена при финансовой поддержке гранта РФФИ № 13-05-00979-a.