Модель распространения вредных веществ и избытков явной теплоты в производственных помещениях

Введение. Повышенная загазованность рабочих зон производственных помещений машиностроительных и ремонтно-обслуживающих предприятий сочетается, как правило, с неблагоприятными параметрами микроклимата (повышенная температура и высокая подвижность воздуха). Так, концентрация вредных веществ в рабочих зонах вблизи действующих источников загрязнения может превышать максимально-разовые ПДК р.з в десятки и сотни раз. А параметры микроклимата в различные периоды года также не соответствуют нормативам. Поэтому не вызывает сомнения, что задача снижения загазованности и сохранения здоровья работников таких цехов при вредном воздействии токсичных выбросов является актуальной.

Для решения данной задачи разработана математическая модель, описывающая процессы тепломассопереноса вредных веществ в объеме производственного помещения, которая позволяет определить опасные зоны загазованности и области с неудовлетворительными параметрами микроклимата, оказывающие негативное воздействие на работников.

Математическая модель тепломассопереноса вредных веществ и избытков явной теплоты. Система уравнений в общем виде. Распространение примесей, движение воздуха (в потенциальном приближении) и изменение температуры в рассматриваемом объеме описывается следующей системой уравнений [1, 2]:

d C i + d ( uC) , d ( vCd , d (( w - w , ) C ) d t      8 x      d y          d z

d d x

( A _m + D ) — ' n x        X '

О X

d

+

5 y

/

к

(А ny + Dy)     1 + dy )

⁺   f ⁽ А n z ⁺ D z ) ^ 1 ⁺ 2 ^Qi^{J (} t ^{) 5 (} r - r j ),

оz к dP     dP u = —, v= —, w = —, dx      dyd d2 P  d2 P  d2 P„

—Г + —г + —T = 0, dx2   dy2

P C p

fd T ₊ d iT ₊ d (VT) ₊ d ( wT ) _к d t     d x       d y      d z

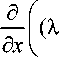
+ X_Z +X_p ) ^ T t ^p d x

r

У я f

) ⁺ d y к ^{( X}

d T 1

+ X_z + X )— I + t ^p 8 y )

+ l ( X +X t +X p ) ^1 + 2 Q V,, ( t ) 5 ( r - rj), d z к              d z )

где X t

C p P Pr d A _n Pr t

– коэффициент турбулентной теплопроводности, отображающий связь ме-

жду коэффициентами турбулентной диффузии помещения; Ci - концентрация i-го вредного вещества в помещении; u,v, w - компоненты вектора скорости воздушной среды; ws - скорость оседания/подъема примеси/газов; Ап = (Ax, Ay, Az) - коэффициенты турбулентного обмена помещения; Dxyz - коэффициенты диффузии; Qi(t)- интенсивность выброса i-го вредного вещества от j-го источника в помещении; 5(r - rj) - дельта-функция Дирака; P - потенциал скоростей движения воздуха; р - плотность воздуха; T - темпера тура; rj = (xj, yj, zj) - координаты источника выброса; u,v, w - компоненты скорости; Cp - удельная изобарная теплоемкость; X - коэффициент теплопроводности; Xp - коэф- фициент радиационной теплопроводности; QVji – интенсивность внутренних источников те- пла; Prd - диффузионное число Прандтля; Prt - турбулентное число Прандтля.

Граничные условия для уравнения (1):

– на боковых стенках

С = о. д n

В этом равенстве указано, что стенки помещения, в котором проводятся исследования, являются непроницаемыми для концентрации загрязняющего вещества;

– на входной и выходной границе дС =- ^с, д n    А п

|u n , и n > 0, где q = <           означает, что поток примеси зависит от ее концентрации, скорости и и на-

[0, u n < 0                                                                                          n правления воздушного потока, индуцированного работой вентиляции.

Граничные условия для уравнения (2):

– на твердых стенках

=о, д n где n - единичный вектор внешней нормали.

Это означает, что стенки исследуемого помещения являются непроницаемыми для воздушных потоков;

– на выходной границе дР

=U n , д n где un - известное значение скорости;

– на входной границе (границе втекания воздушного потока в помещение) Р = const (условие Дирихле).

Граничные условия для уравнения (3) [3].

Начальные условия заключаются в задании распределения поля значений температуры в начальный момент времени ( t =0), т.е. предшествующий расчетному. Они должны быть заданы в виде функции T_t = ₀ = f ( x , y , z ) - для пространственной задачи. Граничные условия - тепловые условия у поверхности тела, которые задаются в более сложном виде. При решении задач тепло- 1032

проводности принято различать четыре часто встречающихся способа задания граничных условий, так называемые граничные условия первого, второго, третьего, четвертого и пятого рода. Граничные условия третьего рода заключаются в задании температуры поверхности тела и окружающей его среды и задании теплообмена (коэффициента теплопередачи) между поверхностью этого тела и окружающей средой по закону Ньютона. Таким образом, количество теплоты, отдаваемое (или получаемое) единицей поверхности температурой T _п за единицу времени в окружающую среду температурой T _с , прямо пропорционально разности температуры поверхности и окружающей среды: q _п = a ( T _п - T _с) [4]. Количество теплоты, отдаваемое (или получаемое) поверхностью в окружающую среду, должно быть равно количеству теплоты, подводимому к этой поверхности за счет теплопроводности, которое определяется по закону Фурье. Приравняв эти потоки, получим новое выражение для задания граничных условий третьего рода:

^{∂ T} = - ^a ( T - T ) .                                     (4)

пс

∂ n     λ _t

В условии (4) должны быть заданы коэффициент теплоотдачи a и температура окружающей тело среды T _с . В ходе экспериментальных работ граничные условия могут быть уточнены.

При турбулентном течении потока и турбулентном переносе коэффициенты А п пропорциональны диссипируемой энергии и определяющему размеру рассматриваемого источника. Для вентилируемых помещений, зная величину энергии, поступающей в помещение, и определяющий размер источника, можно определить коэффициент турбулентного обмена в плоскости ( x, y ) [5]:

Ax =Ay = 0,25ε1 3lп4 3, где ε – кинетическая энергия воздушных потоков в помещении; lп – определяющий размер помещения, равный для прямоугольных отверстий и сечений неправильной формы lп = F , здесь F – площадь сечения помещения, перпендикулярная направлению движения воздушных потоков.

Коэффициент турбулентного обмена по высоте помещения находится из зависимости, предложенной М.Е. Берляндом для наибольших классов устойчивости воздушной среды A _{п z} = A_{z = 1} ( z z ₁ ) , что допустимо для исследуемого помещения. Здесь A_{z = 1} – коэффициент турбулентного обмена на высоте 1 м, z 1 =1 м, z – текущая высота помещения.

Кинетическая энергия воздушных потоков в помещении определяется из формулы: ε = εп.с + εт.с + εд.п - εв.с , куда входят соответственно энергии приточных струй εп.с, тепловых струй εт.с , движущихся предметов εд.п и вытяжных струй εв.с . Величины εп.с ,

ε т.с ,

ε д.п учиты-

ваются в модели рассеивания вредных веществ и находятся из формул:

L

ε п.с

ξν ²

^V п   ²

ε

gQz 1 + n

C p T 0 ρ в 4 ^,

₌ ξ F _п ⋅ ν ³ _п ρ   τ

2 G п 3600 , где L Vп – кратность воздухообмена в помещении свободным объемом Vп ; ν – средняя скорость выхода воздуха из приточных отверстий; ξ – коэффициент местного сопротивления на выходе из воздухораспределителей; Q – теплонапряженность объема; g – ускорение свободного падения; z – расстояние от полюса до рассматриваемой точки; n=0,8 – экспериментальная константа; Ср – теплоемкость воздуха на удалении от источника; T0 – температура воздуха в помещении на удалении от источника; ρв – плотность воздуха на удалении от ис- точника; ξ – коэффициент аэродинамического сопротивления движущегося предмета;

F _п – площадь поперечного сечения движущегося предмета; ν _п – скорость движущегося предмета; τ – средняя продолжительность движения предмета с данной скоростью в течение 1 ч; G _п – масса воздуха в объеме помещения.

Так как G _п = V ρ , где V – объем помещения, то

_{ε =} ξ F _п ν ³_п    τ

.

^д.п 2 V 3600

Явное теплопоступление в помещение учитывается для источников, оборудованных местными отсосами, как

Qя =СpmОaГxQОmГax(ТОmГax-T0)(1-ϕОГ)Ад, а для источников ими не оборудованных

Qmax max max я = С pОГ QОГ (ТОГ - T0)Ад , где С pmОaГx , С pхОГ – изобарные теплоемкости отработавших газов (ОГ) на режимах максимальной на- грузки и холостого хода; Т ОmГax, ТОхГ – температура ОГ на различных режимах нагрузки;

А _д – количество стендов.

Для реализации предложенной математической модели разработано программное обеспечение, реализующее интерфейс, который обеспечивает взаимодействие пользователя с пакетом FlexPDE и базой данных, в которой содержатся все необходимые данные для проведения модельных расчетов. Интерфейс системы создан так, что любой пользователь, имеющий элементарные навыки работы с Windows-приложениями, может без труда работать с программным продуктом.

Результаты модельных расчетов. В предложенной математической модели возможно проведение расчетов для различных схем организации движения газовоздушных потоков в помещениях, а также для штатных и аварийных ситуаций (например, неработающая принудительная вентиляция, разрывы отсосов и т.д.). Численные результаты получены на основе конечноэлементного моделирования системы уравнений (1)-(3). На рис.1, 2 представлены рассчитанные по модели поля относительных концентраций оксидов азота на высоте z=4 м за один час работы обкаточного участка ω поля подвижности воздуха в помещении в зависимости от расчетных пе- риодов года.

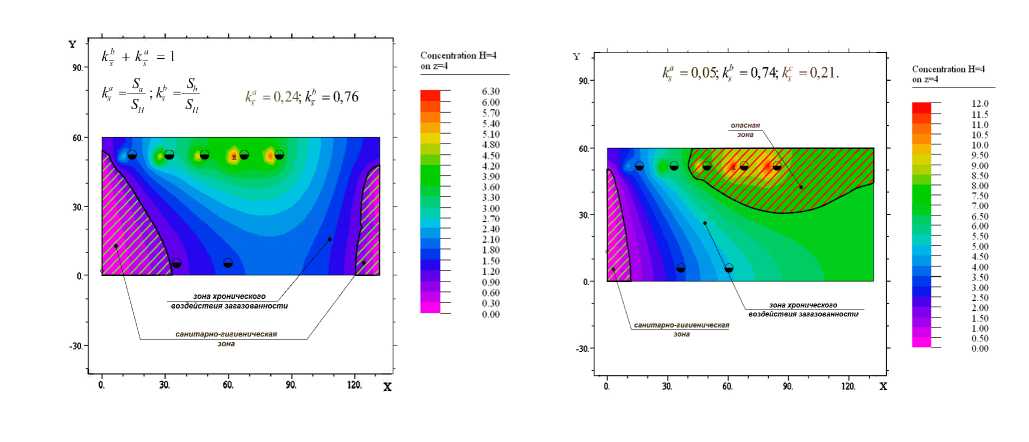
а )                                                           б )

Рис.1. Поля относительных значений концентрации NO x в воздухе участка обкатки на высоте z =4 м в штатном режиме: а – «теплый» период года; б – «холодный» период года

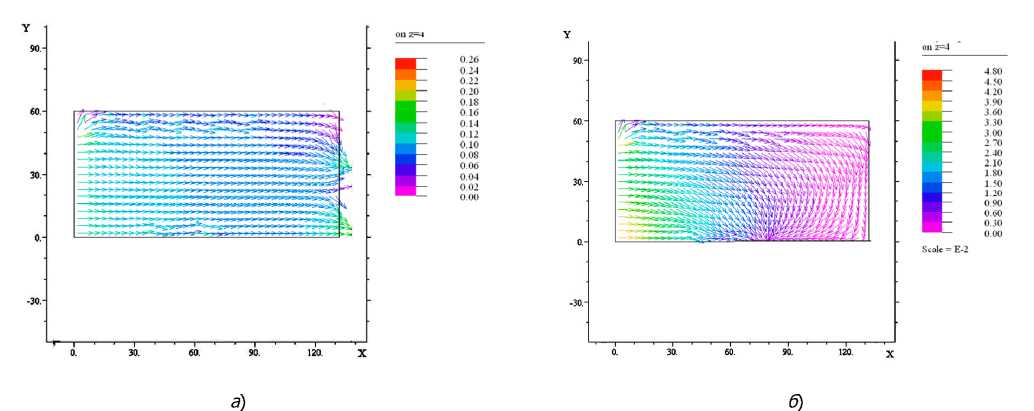
Рис. 2. Поля подвижности воздуха в помещении участка обкатки на высоте z =4 м в штатном режиме:

а – «теплый» период года; б –«холодный» период года

На рис.3 показана динамика изменения относительных значений максимально-разовых концентраций оксидов азота в воздухе помещения на высоте «среза» 4 м в течение одного рабочего часа.

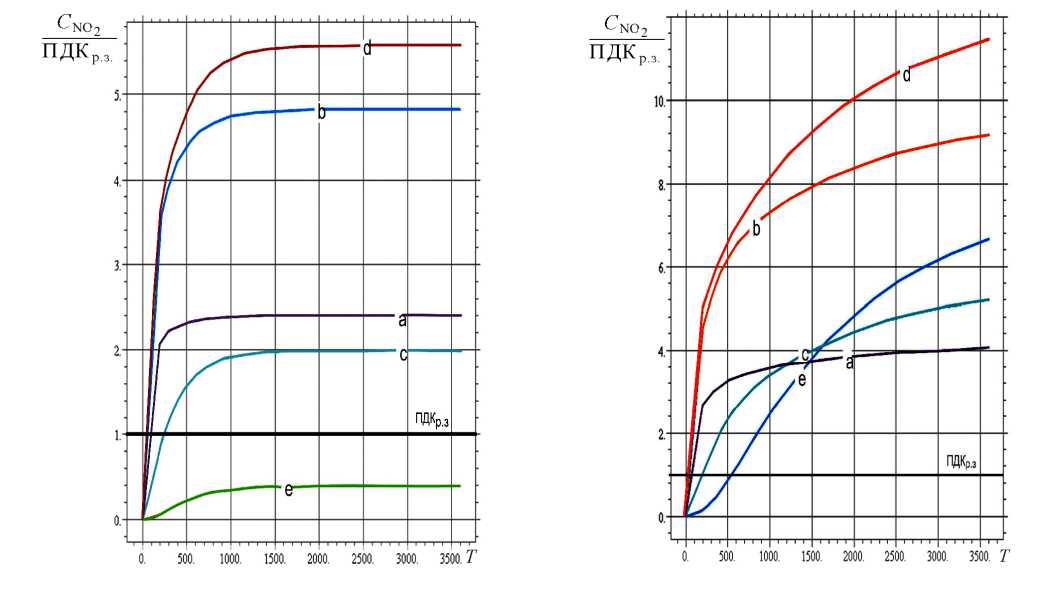
а )                                                                 б )

Рис.3. Динамика изменения относительных концентраций оксидов азота в воздухе помещения участка обкатки в течение одного рабочего часа:

а – «теплый» период года; б – «холодный» период года; а-е – выбранные точки помещения

Выводы. Показана возможность применения разработанной модели для уточненного прогнозирования качества воздуха в рабочей зоне производственных участков; созданное программное обеспечение позволяет оперативно определять опасные зоны загазованности, поля подвижности воздуха и температур для различных производственных участков; результаты моделирования могут быть использованы для определения рациональных мест расположения возду- хораспределителей в системах приточно-вытяжной вентиляции помещений и для выбора мест размещения датчиков газового контроля.