Модель равновесной локализации деформации

Process of strain localization space-modulated pattern formation (among them in form of shear bands) in homogeneously loaded one-dimensional continuum is studied. The material is described by the state equation, which is nonmonotonic on strain and has the second gradient of strain. The gradient term supports the local equilibrium behind the critical point, so the pattern can arise quasistatically.

Изучаются закономерности образования периодической структуры локализации деформации (в том числе и в виде полос сдвига) в однородно нагружаемой одномерной сплошной среде. Материал подчиняется уравнению состояния, не монотонному по деформации и содержащему второй градиент деформации. Градиентный терм обеспечивает локальное равновесие за критической точкой, благодаря которому структура может возникать квазистатически. Такой, авременной, сценарий развития может соответствовать пластичности (равновесному необратимому процессу), в рамках которой дана интерпретация полученного решения. Это недостаточно освещенное в литературе свойство использованного здесь в общем не нового подхода к описанию явления всесторонне и критически исследуется в данной работе.

Пусть одномерная сплошная среда находится в состоянии равновесия:

о' = 0, (1)

где скаляр о — касательное либо нормальное напряжение, а штрих обозначает производную по координате. Из (1) следует однородность напряжения вдоль оси: с(х) = о>0, которое поэтому является приложенным к среде, непосредственно контролируемым параметром нагружения. Рассмотрим определяющее уравнение вида

_Q^f^)^\ (2)

где скаляр е — сдвиговая либо осевая деформация. Функция /: а) проходит через ноль /(0) = 0 и потому обеспечивает у материала наличие ненапряженного и недеформированного (естественного) состояния: Е = О, е* = 0 rz> а = 0 в силу (2), б) немонотонна: вначале возрастает, затем убывает на небольшом отрезке, после чего опять возрастает. Падающий участок описываемого этой функцией силового профиля моделирует внутреннюю нестабильность материала, природа которой обсуждается далее. Простое макрофеноменологическое уравнение состояния (2) предложено более 20 лет назад Э. Айфантисом [1] для уяснения механизма образования структур в духе формализма Ван-дер-Ваальса - Гинзбурга - Ландау. Это уравнение можно воспринимать и как уравнение равновесия для относительного перемещения компонент одномерного двойного континуума [2].

Для качественного изучения данной системы с одной переменной состояния £ и одним управляющим параметром о не имеет смысла задаваться профилем / сложнее катастрофы двойной складки

/(в) = е3 - е (3)

в координатах £,а с началом в точке центральной симметрии этой кривой. Удобнее отождествить начало координат с точкой локального максимума (рис. 1), в таком случае (2) примет вид

Е* + Е3 - V3E2-0^0, (4) если обозначения переменных оставить прежними. Это уравнение имеет кубичную и квадратичную нелинейности.

Для уравнения (4), не зависящего от е' и х, можно записать интеграл энергии (для чего предварительно обе его части следует домножить на г' и использовать равенство eV = j(e'²)'):

1^(£'²)+^[/(8)-q^£ = 0. (5)

Здесь для определенности считалось, что известны значения £₀,Eq в некоторой точке х₀. В (5) можно выделить части, определяемые деформацией (U= f/W8 =

|е⁴ --^-е³), градиентом деформации (G = ~е'²) и напряжением (-ое).

Первые две части составляют “внутреннюю’* потенциальную энергию деформированной точки, последняя — потенциальную энергию приложенного напряжения, а все вместе — полную потенциальную энергию системы. Обозначая

E-G-vU-ОЕ = -t'¹ -г |е⁴ - ^Е³ - OE (6) и Е_о = E(e₀,Eq), уравнение (5) можно записать в виде¹

Е-Е,. (7)

В рамках пластической интерпретации реологии модели (см. конец статьи) энергия Е диссипирует, поэтому независимость ее от х означает однородность диссипации по пространству. При фиксированном о энергетическое состояние определяется только значениями £_о,£о. Далее из всех энергетических состояний, отвечающих одному и тому же о, мы будем выделять состояние с локальным минимумом энергии, называя его состоянием невозмущенного равновесия.

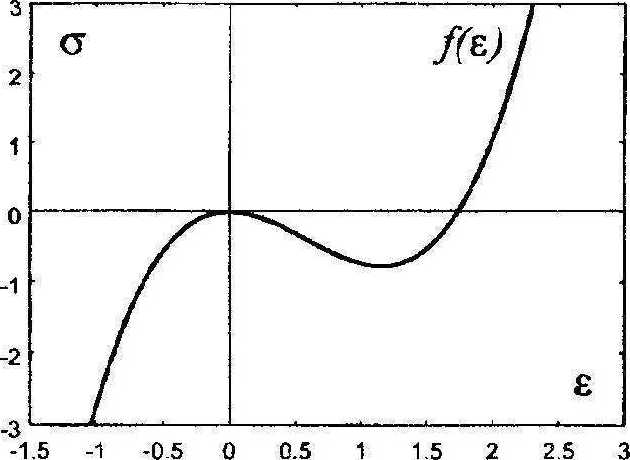
Рис. 1. Начало координат как точка локального максимума

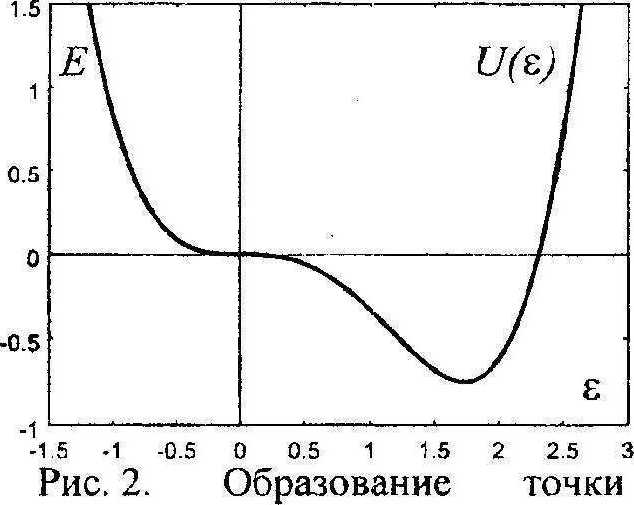
перегиба при слиянии

локального максимума с локальным минимумом

Функция Е задает потенциальный рельеф системы (4), изменяющийся в зависимости от приложенного напряжения. В начале нагружения, когда а<--4-, U имеет один локальный минимум, соответствующий ее абсолютному минимуму, при напряжениях

4 зЛ

<а<0 имеются два локальных минимума и один локальный

максимум и при о>0 опять остается один локальный минимум, являющийся абсолютным, В точках <з-

4 Зл/З

, 0 локальный максимум сливается с одним из

локальных минимумов, образуя точку перегиба (рис. 2). Если нагружение производить весьма осторожно, состояние среды в течение всего этого процесса при о < 0 будет соответствовать точке локального минимума потенциального рельефа (при ^С-^ — абсолютного, а при - ^ < о < 0 — левого локального), а при а = 0 — точке перегиба, и тем самым проходить непрерывный ряд состояний невозмущенного равновесия. Это v dE _ дЕ _л , , эквивалентно выполнению в процессе нагружения условии 7^ "~ Эк7 ™ U

Е³ - V3E² -а = 0, е' = 0 (заметим: требующих однородности решения). Такое нагружение будем называть невозмущенным равновесным.

Исследуем вопрос устойчивости состояния среды в течение невозмущенного равновесного нагружения. Будем называть значения E0,£q, заданные в некоторой точке среды, согласованными с приложенным напряжением, если Ед - Тз£д -а = 0, Ед = 0.

Возмущения в изучаемой системе могут порождаться значениями Е₀,Ед, если они не согласованы с приложенным напряжением. Относительно таких возмущений мы и будем исследовать устойчивость невозмущенных равновесных состояний, для чего сначала воспользуемся интегралом энергии (7). При g<--^- такое состояние

Е = Е0, е' = 0

однородно и устойчиво. При

-^-<о<0 то же решение локально

устойчиво. Некоторые конечные возмущения способны реализовать переход к энергетически эквивалентному в общем неоднородному решению. Заметим, что хотя при " ^|" - ° < ~ ^" заданному а уже могут соответствовать дополнительно одно-два решения уравнения f(E) = G, их реализация с помощью какого-либо возмущения энергетически невозможна. Наконец, при о = 0 однородное решение становится неустойчивым. Итак, если возмущения малы, то при о < 0 решение отклонится от невозмущенного равновесного также мало. При о = 0 малейшее возмущение равновесного однородного решения е s 0 в любой единственной точке сразу повлечет смену решения на неоднородное. Состояние а = 0 назовем критическим.

Исследуем тот же вопрос с помощью уравнения (4). Пусть однородное его решение возмущено: е(О) = е_о+<х, е'(0) = 0, где Е_о согласовано с приложенным напряжением Eq - Тзе^ "<у-0, а а мало. Тогда для малых отклонений ё = е-е₀ из (4) имеем уравнение Ё* + (Зе^ - 27зе₀)ё = (9(Ё²). При су < 0 значение е₀ всегда отрицательно и конечно, поэтому полученное уравнение для малых отклонений с условиями на них в нулевой точке Ё(0) = а, ^(0)-0 описывает волнообразный профиль £ = acosAxc малой амплитудой а и конечной длиной волны к = (3Eq -27зе₀)^1/2. При а^-0 будет Е_о ->-0 при е₀ ^ о^1/2 и А^+0 при к^а, т.е. длина волны становится бесконечно большой. В критической точке а = Е_о=О линейный анализ не дает полной картины происходящего.

Будем считать, что среда равновесно нагружена до критического состояния о = 0, т.е. описывается уравнением г" + Е3 - Vie2 = 0.                                  (4х)

Получим сначала решения системы, соответствующие сепаратрисе — фазовой траектории, проходящей через особую точку поверхности Е^е') при о = 0. Из (6), (7) при а = 0 и Е_о = 0 имеем

2e^/2=e²(^e-e²).                          (8)

Уравнение (8) можно воспринимать и как первый интеграл в критической точке, и как уравнение сепаратрисы на фазовой плоскости ^е') . Интеграл (8) имеет вид х-х0

^ ~у==== - - -ГТ

а обращение его ведет к двум решениям е = О

_4__*_________

^1+|(х-х5)2 ’

(Ю)

где х_б =х₀-х(е₀) определяется нижним пределом (9). Как видно, рассматриваемому нулевому энергетическому состоянию может соответствовать неустойчивое однородное решение (10)] либо устойчивое неоднородное решение (10)₂, возбуждаемое лежащим на сепаратрисе в остальном произвольным ненулевым возмущением. На рис. 3 приведен профиль Е = 1—- неоднородного решения. Полуширина профиля

(т.е. его ширина при половинном значении амплитуды е = -^) равна Тб-2,45. Воспользуемся фазовой плоскостью (рис. 4). Критическая точка расположена на конце острия и соответствует однородному решению. В этой точке интеграл (9) имеет сингулярность (в точке е = -^, кстати, сингулярности нет). Обходя сепаратрису, получаем неоднородное решение (10)2, причем первая половина пути, от конца острия до середины тыльной части £ = 4-, е' = 0 (максимума профиля г(х)^-), равно как и вторая его половина, соответствуют бесконечному изменению координаты. Если такой обход совершается с постоянной скоростью, т.е. в каждый момент скорость движения по касательной к сепаратрисе постоянна, то скорость изменения координаты х вблизи критической точки возрастает до бесконечности. То есть амплитудное значение возмущенного неоднородного решения реализуется на некотором расстоянии л₆ от точки х₀ , неограниченно растущем по мере уменьшения возмущения.

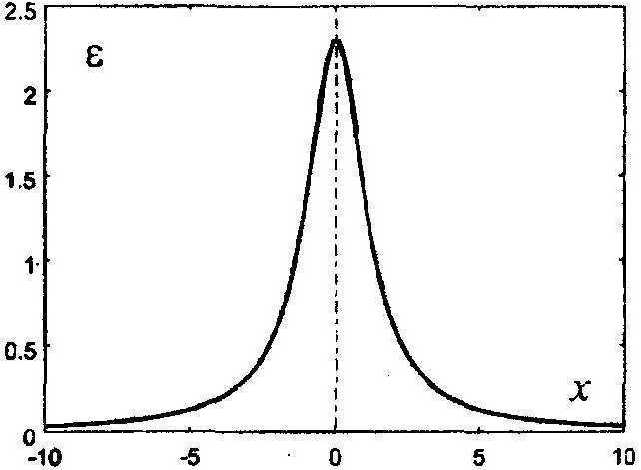
Рис. 3. Профиль неоднородного

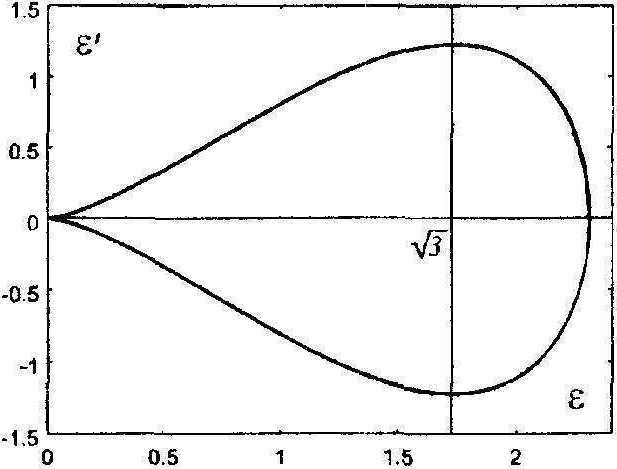
Рис. 4. Фазовая плоскость

решения

неоднородного решения

Получим теперь возмущенное решение, полагая £0 =а, Eq - 0, где а — малая величина положительного или отрицательного знака, слегка уменьшающая или увеличивающая энергию системы. Из вышесказанного логично ожидать, что такое решение уравнения нелинейного осциллятора (4*) будет периодическим и состоять из чередующихся протяженных участков с £~0 и локализованных всплесков с амплитудой е«4-, причем при а-эО период должен неограниченно расти, а полуширина каждого всплеска достигать значения V6 , то есть возмущенное решение должно стремиться к решению на сепаратрисе (10)2. Вблизи е = 0

g(E) = £⁴ -4-е³ =— т“Е³+О(е⁴) и корни g(E) = 4-a³ суть a₂ ~-a +(9(а^{4 3}) и

*   '          уЗ V3                                         уЗ

Р ± /у = 4 а(1 + V3Z) + О(сх^{4/ 3}). Второй действительный корень a_f уравнения g(e) = g(a₂) равен a, = -4 + O(a³). Решение (4') тогда записывается в виде [3]

уЗ cq + а2 0^ - а2 v - cos

2         2    1- vcos

07 - 9.   67 + 0i Jcos0icos02 17     ? 9 - 0- v = tg —--Ltg^--Е р = -^--------, F=sin2^--

2 2й у         2

где

Л а, - В а7 - В tg9,=^-^, tge2=^-^_ Y            Y вспомогательные величины. К сожалению, эти формулы содержат ошибки. Решение (11) дает описанный выше профиль только при v»l, при этом пики всплесков соответствуют точкам, в которых cn = 1. Для получения такого решения некоторые из приведенных выше формул были изменены следующим образом:

v = tg

^1 ~ ^2 2

02 + 0

к² =sin²

6] + 62

причем знаки углов 012 следует изменить так, чтобы эти углы стали острыми,

0 < 0{ 2 ^з - С помошью этих определений получаем

0) = arctg^ = ~-0,375| а|+б)(а2), 02 = arctgV3 = у, v = tg(^- - 0,1875a)tg(^ - 0,1875а) = 1 -1,5а + О(а2),

^^sintO^Sa^)172^-1 =Ч),5а^

к = sin(§) + О(а) = ^^ + О(а) = 0,97 + О(а).

Точка V = 1 — особая для (И), поэтому для v был взят первый порядок разложения, для модуля к был взят нулевой порядок, поскольку для эллиптического интеграла первого рода точка к = 0,97 не является особой (особой же является точка к = 1). Решение (11) принимает вид

2     1 -1 а - сп(V^x~2K(£),£)

е = -р (1--—----- 7= ---------) + О (а).

V3    1 - (1 -1 а)сп( 41а.х - 2К(£), к^

При   а—>0   в точках   х = у V2K(^)a 1/2, у = ±1,±2,... получим, устраняя неопределенность, Е—»Д. В точках х = у-4-К(Л)а 1/2, у = ±1,±3,... при а-»0 е—>0.

Профиль решения при а = 0,01 показан на рис. 5. Его период по шкале х, 2>^К(^)а*1/2 (КОД-3,1), неограниченно растет при а->0. Однако полуширина всплесков при этом остается ограниченной, в пределе достигая значения -Тб . Чтобы в этом убедиться, сначала следует разложить cn(V2a^) = l -ax2 + (?(a2x4) в ряд вблизи сп = 1, затем заметить, что полуширина соответствует нулевому значению числителя дроби в (12), откуда получить координаты х± =±^ искомых точек.

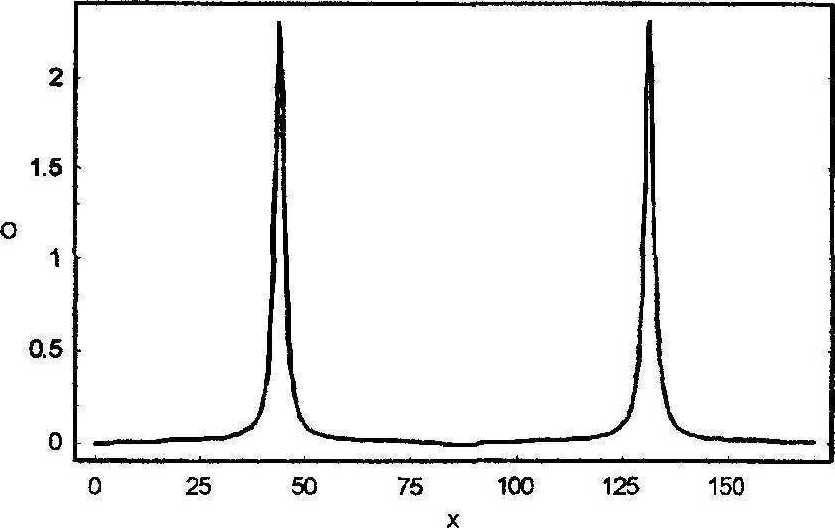
Рис. 5. Профиль решения при а = 0,01

Правильность решения подтверждается численным интегрированием уравнения (4^х) с использованием пакета «Математика», обнаруживающим все отмеченные свойства. Отметим, что период оказывается несколько заниженным по сравнению с аналитически найденным значением, однако с уменьшением е₀ различие также уменьшается, составляя, например, 7,4% при е₀ — 10~^б. Причина расхождений — сугубо численная и определяется минимальным шагом интегрирования вблизи особой точки.

Параметры v,p,£ решения (12) могут быть получены и без каких-либо формул путем подстановки его в (4х) при р = 1 - v »< ос и ц ^ (а)-1/2 . Представляя (11) в виде

1 ± и z ------ w — спОХ ,

1 ™ VM

e = |(-^-G-v)z₊ -a(l+v)z_).

получаем

,     ±1 + V ,    ,    ±1 + V - '2 .

z₊ -------- -u , z₊ =--------(2vw + (1 - ^u^u ), ~ (1-vm)²         (1-vk)³

Далее,

Е3 - ^е2 =             - V) + а(1 + v)]cn + ^(1 - v) - а(1 + v))2 х

x([2V3v + -^ (1 - v) + а(1 + v)]cn - 2V3v + -4Д1 - v) - a(l + v)).

v3                                V3

Подставляя все в (4х), приравнивая коэффициенты при степенях сп и используя соотношения между малыми величинами, получим систему

JjpCT2p_^(^.p + 2a)2 =O(a3X

-^-ро2(2А2   + (—12a2 -Ма$ + 4У O(a3),

4фо2(2£2 -l) + ^(12a2 -^aP-W) = O(^

^ pa2 (1 - ^) - ^ (^ p _ 2a)2 = O(a3).

Разность второе и третьего уравнений дает р-^а. Разность первого и четвертого уравнений дает п²(2£² -1) = 73а, а их сумма — 2о²р = 2р²+|а². К последнему уравнению также приходим, суммируя второе и третье. Окончательно v = 1 -1 а, <5- V2a_? к = ^^ с точностью до малых более высокого порядка.

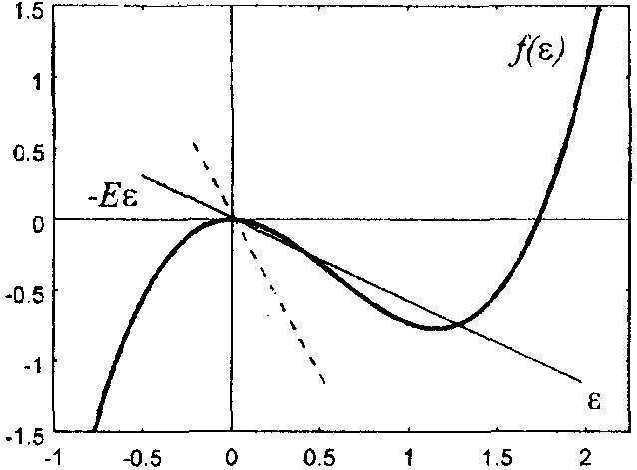
Рис. 6. Графическое изображение уравнения (13)

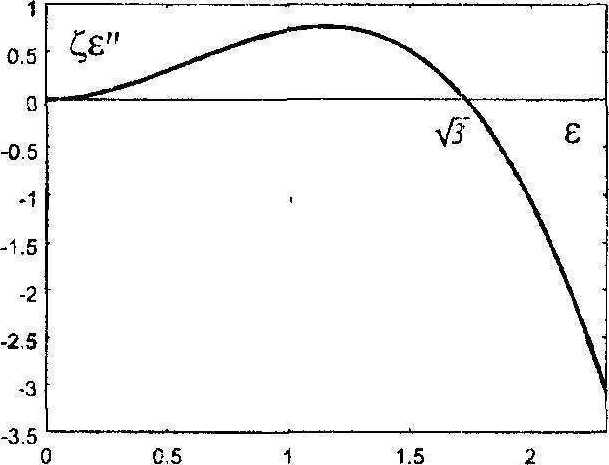
Рис. 7. Равновесная траектория перехода в новое состояние

Выше исследована реакция материала на мягкое нагружение, осуществляемое приложением напряжения. Далее рассмотрим нагружение конечной жесткости. Пусть тонкий слой изучаемого материала нанесен на упругую полосу и неразрывно с ней связан. Для малого элемента такой одномерной системы принимаются гипотезы

Е|=е2=Е, xoiM-Xfe^a, где г, о — деформации и напряжения в элементе, а ер о, — в его упругой (индекс 1) и нестабильной (индекс 2) компонентах, % — относительная доля упругой составляющей в поперечном сечении элемента, а сама эта система по-прежнему полагается нагружаемой приложением напряжения о. Принимая в качестве уравнений состояния ох=Егъ о2=Ж)

и обозначая Т               , получим

.          т = /(Е) + це.                                    (13)

Это уравнение изображено графически в момент, когда приложением напряжения о к элементу значение т доведено до критической точки кривой / (рис, б). Правая часть (13) соответствует разности функций f (г) и -ре. Поэтому, кроме уже изученного случая р = 0, указанный момент еще не является критическим для всей системы. Исследуемый нестабильный материал следует рассматривать совместно с нагружающим устройством — упругой основой. Очевидно критический момент (рис. 6)

/^«-а соответствует некоторому повышению напряжения и деформации. Отождествляя начало координат с критической точкой и оставляя прежние обозначения для новых переменных, уравнению (13) для случая р < 1 может быть придан вид

Е3 - ТЗКЕ2 - Т = 0, где к = 71 Ц • Локальная внутренняя энергия деформаций запишется как

• --i ке³ -те.

• ⁴ 7з

В рассматриваемый момент т - О происходит бифуркация: наряду с основным решением е₀ - 0 появляется новое е*=7зк. Имеем 1/(е_о) = О, <7(е») = -|к⁴, следовательно, система скачком переходит в новое состояние, при этом теряя (выделяя) энергию, зависящую от жесткости нагружения. При жесткости р>1 бифуркации отсутствуют, что иллюстрируется на рис. 6 штриховой линией.

Если вместо о₂ " /(^£2) берется уравнение состояния (2) су₂ = /(£2) ^{+ e}L ^то решение (12) несколько изменится:

2к    1-Д-а-сп(Т2ах-2К(^)Л)

Е = ——(1--—-------—---------) + О(а),

к У2+У3к                                           .

где к - —5— ■ ПРИ увеличении жесткости до р = 1 амплитуда периодических всплесков уменьшается до нуля пропорционально У1-р , а их полуширина растет как

Уб

4/iZi7 > то есть профиль как бы расплывается.

Если уравнение (2) содержит константу £ > О при градиентном составляющем, то (4’) перепишется в виде

Щ+е3-м2=0.                    (4”)

В решении (12) тогда изменится только волновое число а = —^-5 так что при ^—>0 период профиля и полуширина всплесков стремятся к нулю со скоростью ^ С//2. При этом можно увидеть тенденции дезинтеграции сплошной среды на невзаимодействующие материальные точки. При ^ ^ О градиентный терм (точнее, оператор Лапласа) организует эти изолированные точки в структуру.

Уравнение (4^й) задает равновесную траекторию перехода в новое состояние, содержащуюся в сечении а = 0 поверхности о^е,е") (рис. 7). Следует обратить внимание на то, что точка е - 7з оказывается амплитудным значением нового состояния только в случае £ = 0 (само это состояние есть £ = ^), в других же случаях, сохраняющих энергию при переходе, эта точка соответствует точкам перегиба решения г(х)₃ амплитудное значение £ = ^ которого не зависит от £. Конечно, состояние далеко не всех точек среды заметно “продвигается” вдоль этой кривой при структурном переходе, а в основном только тех, что находятся в узко локализованных зонах.

Поддерживаемое моделью равновесие в течение развития структуры позволяет предположить, что такой процесс происходит квазистатически, по шкале собственного локального времени точки среды. Такой ход процесса характерен для атермической пластичности, с которой, вероятно, и следует связывать рассмотренную в работе модель. Пусть в качестве материала для определенности рассматривается металлический кристалл с большим количеством решеточных дислокаций. В рассматриваемом одномерном случае атомная решетка, испытывая упругие деформации, передает усилие неупругой компоненте, в качестве которой фигурирует система дислокаций. Будем считать, что скольжение последних производит только атермические пластические деформации, что для металлических кристаллов справедливо для не слишком высоких температур и не очень длительных испытаний, когда термофлуктуации не оказывают заметного влияния на процесс. Спонтанные события самоорганизации дислокаций временно понижают напряжение, требуемое для квазистатического деформирования кристалла с постоянной и малой скоростью, что в ходе такого процесса приводит к образованию ямок на кривой нагружения, символизирующих нестабильность материала. Таким образом, мы должны записать аддитивность упругих и пластических деформаций

Е- 4-Х

и отождествить деформации ранее изученной модели с пластическими деформациями:

o-/(X)^V.

Из сказанного о природе ямок совсем не следует, что моделируемая этими уравнениями среда должна подвергаться именно жесткому нагружению. Особенность модели заключается в том, что квазистатичность процесса возможна при любой жесткости нагружения. Поскольку приложенное напряжение непосредственно действует на оба реологических элемента, упругий и нестабильный, критические моменты, определяемые в рамках прежней и переформулированной моделей, совпадают. При критическом напряжении о = о4 в течение авременного переходного процесса образования структуры реализуется определяемое (15) приращение пластической деформации ДХ с профилем (12), вызывающее согласно (14) аналогичное приращение полной деформации. Профиль упругой деформации а* / Е при этом остается однородным. Уравнения (14), (15), конечно, могут описывать лишь активный режим нагружения упруго-пластической среды и быть справедливыми для процессов, не сопровождающихся упругими разгрузками. Но в рассмотренной задаче активность нагружения в каждой точке сплошной среды гарантирована.

Если а отождествить с касательным напряжением, а е — со сдвиговой деформацией, то элементы образующейся структуры следует интерпретировать как полосы сдвига. В металлическом кристалле такие полосы представляют собой пластиновидные области с большой интенсивностью сдвиговой деформации в них вдоль их плоскостей. Данные плоскости не совпадают кристаллографическими плоскостями, и поэтому такая мода деформации активизируется во вполне реальной ситуации, когда фрагмент кристалла не может далее деформироваться кристаллографическим скольжением по причине жесткости нагружающего устройства или окружения [4]. Поскольку сдвиги по некристаллографическим плоскостям неизбежно нарушают порядок атомной решетки, их локализованность (т. е. тонкость по отношению к расстоянию между ними) отражает стремление кристалла при его деформации максимально сохранить структуру своей решетки — энергетически оптимальной конфигурации взаимодействующих атомов. Деградация решетки сильно увеличивает ее внутреннюю энергию, поэтому локализация таких мест внутри узких полос, разделяющих практически ненарушенные области, минимизирует внутреннюю энергию кристалла. Строение макрополос сдвига исключительно аккуратно исследовано в [4]; они представляют собой матричный композит с включениями-каналами или субзернами с оптимальной ориентацией решетки к площадкам наибольшего касательного напряжения, отделенными от матричного материала полос дислокационными границами ориентационного несоответствия. Следовательно, природа формирования полос сдвига тесно связана с коллективными дислокационными процессами, в ходе которых решетка в некоторых малых областях поворачивается так, что касательное напряжение на одной из кристаллографических систем скольжения увеличивается, пока не достигнет максимального. При этом дислокации выстраиваются в стенки и другие планарные образования, отделяющие упомянутые малые области (каналы и субзерна) от остального кристалла и обеспечивающие ориентационное несоответствие решетки. Поскольку упрочнение металлического кристалла на этой стадии очень невелико, малое повышение касательного напряжения на действующей системе скольжения внутри каналов и субзерен приводит к большому сдвигу. Сдвиговая деформация полосы сдвига при этом оказывается конечной. Все эти экспериментально зафиксированные факты отражает исследованная здесь простая феноменологическая модель — и энергетически оптимальное перераспределение диссипирующей внутренней энергии при образовании структуры внутри узких полос, и периодичность, и конечность амплитуды сдвиговой деформации полос. Практически очевидно, что учет нелинейности в ранее исследованной авторами модели фрагментации зерен поликристаллического металла [5] (сводящейся к нестабильному континууму Коссера) должен устранить нереалистичную диффузность, размытость описываемых ею границ фрагментов сдвигов и поворотов решетки.

Похожие картины полос локализации деформации наблюдаются при деформировании сыпучих сред и горных пород [6]. Пластичность при деформировании таких материалов возможна только при наложении гидростатического давления

(которое для горных пород должно быть весьма высоким), сжимающего образующиеся плоскости сдвига и предотвращающего раскол вдоль них. В отличие от металлов пластические деформации в таких материалах, видимо, вообще связаны исключительно с возникновением локализованных полос сдвига. В момент образования полос напряжение, требуемое для дальнейшей деформации, отнесенное к этим полосам, падает. В металлах роль фактора, сжимающего кристаллографические плоскости скольжения и обеспечивающего дальнейшее пластическое течение без разрушения, выполняет электронный газ [7]. Благодаря тому, что данное свойство электронного газа не зависит от температуры, на пластические свойства металлов практически не влияют понижения температуры в интервале от одной трети температуры плавления до наиболее низких достигнутых температур. При повышенных температурах к такой атермической компоненте неупругой деформации прибавляется вязкая, в активизации которой важную роль играют термофлуктуации. Конечно, плоскости сдвига не отождествляются с кристаллографическими плоскостями, хотя бы потому, что скольжение дислокаций не разрушает атомную решетку, однако, как выше было показано, механизм образования полос сдвига во многом обязан этому скольжению. Как в металлах, так и в сыпучих средах и геоматериалах образование полос сдвига сопровождается нарушением порядка и увеличением внутренней энергии среды и потому сосредотачивается в узко локализованных местах.

При нагружении модельной среды до критического уровня ход процесса деформирования во времени определяется темпом нагружения. Но критическому напряжению соответствует процесс развития структуры, который, как и в идеальной пластичности, не может быть прослежен в физическом времени. Между тем, высказанные выше представления о физике пластичности ничего не говорят ни о равновесности закритического процесса, ни даже об обязательности введения градиентного терма для описания образующихся в таком процессе квазипериодических локализованных структур. Как показали авторы работы [8], регулярность таких структур может вызываться способом приложения нагрузки к исследуемому фрагменту среды, вызывающим неоднородность поля напряжений с максимумом посередине этого фрагмента. Если максимальное напряжение больше критического, фрагмент дробится, и т.д. Анализ способов нагружения реальных опытов над металлическими монокристаллами (например, использованных в [4]) и влияния окружения зерна деформируемого поликристалла [9] действительно выявляют условия реализации такого механизма, с успехом использованного в [6] для объяснения периодичности структур полос сдвига в сыпучих средах. Добавление градиентного терма в модель в общем ничего не меняет в таком сценарии, а только сглаживает область, разделяющую части фрагмента. Роль градиентного терма таким образом сводится не к модулированности образующихся структур (период которых в модели изменяется по мере повышения напряжения над критическим и потому необъективен), а главным образом к обеспечению равновесности закритического процесса. С экспериментальными же исследованиями неравновесности закритического процесса мы не знакомы. Можно ожидать, что при конечной температуре термофлуктуационная (т. е. вязкая) доля неупругой деформации тем больше, чем приложенное напряжение выше равновесного. При достаточно мягком нагружении такая ситуация в закритической области как раз и реализуется. Однако экспериментальная проверка неравновесности закритических процессов локализации деформации за счет самоорганизации дислокаций затрудняется микроскопическими размерами исследуемых объектов. Даже если на микроуровне эти процессы имеют скачкообразный характер, из-за малости их масштабов на макроуровне эти скачки не проявляются. Поэтому пока мы должны признать вопрос о равновесности реального процесса локализации деформации, и следовательно, о роли градиентных сил, дискуссионным. Мы рассчитываем получить некоторую ясность в этом вопросе с помощью имитационного моделирования самоорганизации большого числа дислокаций [2].

Авторы признательны профессорам Э.Л. Аэро, А.Н. Булыгину и В.И. Ерофееву за консультации по нелинейным вопросам. Работа выполнена при частичной финансовой поддержке из средств грантов 01-01-00440 Российского фонда фундаментальных исследований и РЕ-009-0 Американского фонда гражданских исследований и развития (АФГИР).