Модель разрушения древесностружечных плит при растяжении перпендикулярно пластин

Древесностружечные плиты, как известно, состоят из частиц измельченной древесины, консолидированных с помощью связующего, в качестве которого используют фенолформальдегидные или менее токсичные смолы [1], [9]. К настоящему времени исследованы возможности совершенствования технологии ДСтП [8], соотношение плотности и прочности [7], влияние модификаторов клеевого раствора [3], [4], [6] и другие аспекты [5], [11]. К недостаточно изученным относятся задачи о влиянии фракционного состава частиц измельченной древесины, используемой для изготовления ДСтП, на их прочностные свойства. Из всего комплекса появляющихся в этой связи вопросов в данной статье рассматривается методика сравнительной оценки прочности ДСтП при растяжении перпендикулярно пласти. Стандартные методы определения предела прочности базируются на механических испытаниях образцов ДСтП [2], [10].

Рис. 1. Фрагменты плиты после разрушения

Однако остается актуальной задача прогнозирования прочности плит в зависимости от гранулометрического состава измельченной древесины.

Гранулометрический состав измельченной древесины, очевидно, влияет на структуру материала плиты, которая, в свою очередь, определяет прочность при разрушении. Чтобы повысить прочность плиты, в частности при использовании измельченной низкокачественной древесины, используют модификаторы стружечно-клеевых композиций [3]. Получаемые при этом результаты не всегда подтверждают эффективность модификации. На это обстоятельство обращается внимание в статье [6], в которой сформулировано предположение о том, что прочность ДСтП на основе модифицированной стружечно-клеевой композиции зависит от структуры материала плиты: если материал имеет четко выраженную гетерогенную структуру, то его прочность меньше по сравнению с материалом, имеющим квазигомогенную структуру. Для проверки этого предположения и получения количественных оценок необходима соответствующая математическая модель разрушения. Обратимся к интерпретации выполненных экспериментов [6].

Два фрагмента плиты, разрушенной в экспериментах при растяжении перпендикулярно пла-сти по стандартной методике [2], представлены на рис. 1.

Предположим, что все частицы имеют форму эллипсоидов с полуосями a , b , c (рис. 1–3). Рассмотрим возможный механизм контактного взаимодействия двух условных слоев древесных частиц, которые разделены поверхностью разрушения плиты. Эти два слоя в поперечном сечении плиты схематично показаны на рис. 3. В сечении плиты на рис. 3 каждая частица одного слоя имеет в предполагаемой поверхности разрушения две точки контакта с частицами дру-

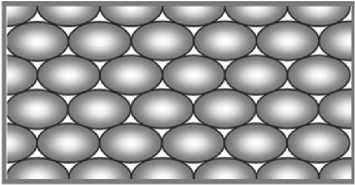
Рис. 2. Модель фрагмента плиты до разрушения

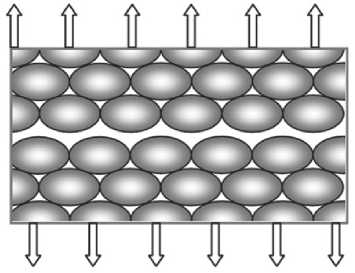
Рис. 3. Модель разрушенного фрагмента гого слоя. Это двухмерный случай. В рассматриваемом далее трехмерном случае каждая частица будет иметь в предполагаемой поверхности разрушения как минимум три точки контакта с частицами другого слоя.

Пусть n – количество частиц одного слоя, контактирующих в точках предполагаемой поверхности разрушения с частицами другого слоя. Тогда в трехмерном случае минимальное число контактов в указанной поверхности N_k = 3 n .

Рассмотрим некоторый фрагмент плиты площадью A, в котором количество частиц одного слоя по рис. 3 равно n. Пусть A1 – площадь проекции одной частицы на срединную плоскость плиты, причем A1 << A. Тогда в трехмерном случае площадь проекции всех частиц одного слоя по рис. 4 равна nA1. Примем во внимание пустоты между частицами и введем в рассмотрение безразмерный коэффициент заполнения p, который по своему геометрическому смыслу принимает значения 0 < p < 1. Приближенно коэффициент заполнения p можно определить следующим образом. Пусть проекции всех частиц имеют форму эллипса с полуосями a и b. Тогда площадь проекции одной частицы A1 = πab. Предположим далее, что проекция каждой частицы вписана в прямоугольник со сторонами 2a и 2b. Тогда p = πab/4ab = 0,785. (1)

Приближенно считаем, что значения коэффициента заполнения p одинаковы как для прямоугольника, так и для всей площади A .

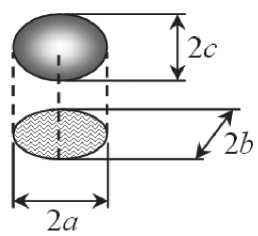
Рис. 4. Проекция модельной частицы на горизонтальную плоскость

По геометрическому смыслу задачи pA = nA1.(2)

Тогда число частиц в одном слое по рис. 3

n = pA IA 1,(3)

а минимальное число контактов этих частиц

N= 3 n = 3pA IA 1.(4)

С учетом равенства (1) перепишем формулу (4), учитывая, что A ₁ = πab :

Nk = 3 • 0,785A / nab = 0,75A I ab.(5)

Очевидно, чем больше количество контактов частиц одного слоя, соприкасающихся в точках предполагаемой поверхности разрушения с частицами другого слоя (рис. 3), тем больше прочность плиты. Эта закономерность следует из формулы (5).

Формула (5) получена в предположении, что объем исследуемой плиты существенно превышает объем наиболее крупной древесной частицы. Это означает, что величина A в формуле (5) должна быть достаточно большой. Пусть A = 100 мм².

Формула (5) получена в предположении, что все частицы одинаковы. Однако используемые для изготовления плит древесные частицы неодинаковы по своим размерам. При этом для крупных частиц количество контактов меньше, чем для мелких. В целом суммарное количество контактов в плоскости разрушения можно рассматривать как параметр прочности при растяжении перпендикулярно пласти плиты.

Можно прогнозировать, что поверхность разрушения пройдет через окрестности тех областей в объеме плиты, в которых число контактов минимально. Такой прогноз будет приближенным, поскольку предполагает, что прочность всех контактов одинакова.

Предлагаемый параметр прочности плиты обозначим как R . Пусть C_i – массовая доля (концентрация) частиц фракции i , N _k ^{( i )} – количество контактов частиц данной фракции по формуле (7), m – количество фракций. Тогда

Оценка прочности в виде (6) является приближенной и не позволяет составить представление о прочности отдельно взятой плиты. Однако параметр (6) может быть рекомендован для сравнительной оценки прочности двух и более плит.

Формула (5) получена для дискретного случая, когда количество фракций равно m . Размеры же стружки являются непрерывными величинами. Введем коэффициент α , определяющий соотношение осей эллипсоида α = a/b , тогда число контактов с учетом (5)

N_k = 0,75 AI aa \              (7)

Пусть f(a)   – плотность распределе ния длины древесной частицы a. Тогда ai

C i = J f ( a ) da ” f ( a i ) ^A a , где A a = ai — ai _-1, или a i - 1

Δa = (a   – a )/m, a и a – наименьший max min        min max и наибольший размеры стружки соответственно.

Если ∆ a → 0( m →∞ ) , то

R = J Nk (a,a)f (a)da.(8)

a min

С учетом (7) при α = const получим:

R = 0,75A [/(О)da.(9)

α amin

Выражения (7) и (9) показывают, что с уменьшением размеров частиц количество контактов между ними увеличивается. Это приводит к повышению прочности.

Рассмотрим применение формулы (9) для сравнительной оценки прочности среднего и наружных слоев древесно-стружечной плит, экспериментально исследованных в работе [6].

В табл. 1 и 2 приведены данные [6] о фракционном составе древесных частиц, использованных для изготовления среднего и наружных слоев ДСтП, а также результаты вычислений по (5) и (9). Сравнивая показатели прочности материала среднего ( 874 ) и наружного ( 6459 ) слоя плиты, можно прогнозировать, что закономерно разрушится средний слой. Этот прогноз подтвержден экспериментами [3], [4], [6].

Важно подчеркнуть, что предлагаемый показатель прочности (9) вычисляется в расчете на единицу площади и пригоден только для сравнительной оценки прочности плит. На необходимость сравнительной оценки прочности плит в зависимости от качества измельченной древесины указывается в ряде работ, например в [8]. В статье [5] показана актуальность исследова-

Таблица 1

Влияние фракций древесных частиц на прочность среднего слоя плиты

Номер фракции, i	2 a , мм	2 b , мм	NK. при A = 100 мм2	Массовая доля (%) и концентрация частиц (в скобках)	Вклад фракции i в прочность R	Относительный вклад фракции i в прочность плиты (%)
1	5	3,5	17,2	24,9 (0,249)	4,3	0,5
2	3,15	2,1	45,2	17,3 (0,173)	7,8	0,9
3	2	1,1	34,1	29,8 (0,298)	10,2	1,2
4	1	0,6	500	21,9 (0,219)	109,5	12,5
5	0,5	0,3	2000	4,1 (0,041)	82,0	9,4
6	0,2	0,1	15 000	1,2 (0,012)	180,0	20,6
7	0,1	0,05	60 000	0,8 (0,008)	480,0	54,9
Итого				100 (1)	874	100

Таблица 2

Влияние фракций древесных частиц на прочность наружного слоя плиты

Номер фракции, i 2a, мм 2b, мм Nk при 100 мм2 Массовая доля (%) и концентрация частиц (в скобках) Вклад фракции i в прочность R Относительный вклад фракции i в прочность плиты (%) 1 5 3,5 17,2 0 0,0 0,0 2 3,15 2,1 45,2 0 0,0 0,0 3 2 1,1 34,1 0,2 (0,002) 0,07 0,0 4 1 0,6 500 12,5 (0,125) 62,5 1,0 5 0,5 0,3 2000 44,4 (0,444) 888 13,7 6 0,2 0,1 15 000 32,6 (0,326) 4890 75,7 7 0,1 0,05 60 000 10,3 (0,103) 618 9,6 Итого 100 (1) 6459 100 ний по совершенствованию технологии производства ДСтП и обосновывается необходимость расширения номенклатуры сырьевой базы за счет рационального использования низкокачественной древесины и обоснования составов стружечно-клеевых композиций [1]. Однако для достижения этой цели необходимы методики прогнозирования прочности плит в зависимости от фракционного состава измельченной древесины. Один из возможных критериев прочности в виде (9) предложен в данной работе. Вычисления могут быть выполнены в табличной форме с применением стандартных инструментов Microsoft Office Excel, по аналогии с приведенными выше табл. 1 и 2.

Результаты сравнительной оценки прочности ДСтП в зависимости от фракционного состава с использованием предложенного критерия подтверждают сформулированное в работе [6] предположение о том, что если материал имеет четко выраженную гетерогенную структуру, то его прочность при растяжении перпендикулярно пласти меньше по сравнению с материалом, имеющим квазигомогенную структуру.

Влияние фракционного состава древесных частиц на прочность ДСтП при изгибе предполагается определить в дальнейших исследованиях. Итоги выполненного исследования дают основания для следующих выводов.

• 1.    С применением экспериментальных данных предложена и обоснована методика сравнительной оценки прочности ДСтП при растяжении перпендикулярно пласти плиты. Методика может быть рекомендована для прогнозирования влияния фракционного состава частиц измельченной древесины на прочность плит.

• 2.    В качестве материала для ДСтП можно использовать низкокачественную древесину. При этом компенсировать относительно небольшое сопротивление частиц измельченной низкокачественной древесины можно за счет увеличения доли мелких частиц, а для прогнозирования прочности плит в зависимости от фракционного состава измельченной древесины использовать предложенный критерий.

• 3.    Установлено, что вклад наиболее крупных частиц в прочность плиты при растяжении перпендикулярно пласти существенно меньше вклада мелких частиц.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.