Модель шестиугольной призматической фермы. Спектр частот колебаний

• 1    Введение / Introduction

Расчет пространственных ферм в инженерной практике, как правило, производится в специализированных пакетах, основанных на методе конечных элементов [1]–[3]. Аналитических решений в виде конечных замкнутых формул, удобных для расчета прогиба, прочности или собственных частот колебаний немного и в основном это решения для статически определимых плоских ферм. Особенно актуальны формульные решения для регулярных ферм, включающие в расчетные формулы порядок регулярности конструкции, например, число панелей. Для вывода формул зависимости решения от числа панелей наиболее эффективен метод индукции, основанный на обобщении серии аналитических решений для ферм с последовательно увеличивающимся числом панелей. При этом общие члены расчетных формул получаются из решения рекуррентных уравнений с использованием возможностей операторов систем компьютерной математики, например, Maple, Maxima или Mathematica. Известны также и другие подходы к получению аналитических решений. В [4], в частности, используется метод суперпозиции, основанный на методе начальных функций, и метод, построенный с использованием функции Грина в виде ортогонального ряда. Разложение по начальным функциям с использованием системы Maple применяется и в [5] для получения аналитического решения задачи о микрополярном прямоугольнике. Балочная аналогия и метод конечных элементов при расчете пространственной модели антенны для космической связи Kirsanov, M.

Model of a hexagonal prismatic truss. Oscillation frequency spectrum;

использовались в [6]. В справочнике автора [7] собраны решения задач о прогибе плоских статически определимых балочных, арочных и рамных регулярных ферм. Аналитический расчет прогиба плоских регулярных ферм с произвольным числом панелей в системе Maple выполнен в [8]–[10]. Оценки первой собственной частоты в виде компактных формул получены методом индукции для ферм [11]–[13]. Проблемы существования статически определимых регулярных ферм и их расчета впервые подняли Hutchinson R.G. и Fleck N.A. в [14], [15]. Рассмотрены общие вопросы регулярных конструкций и решены задачи их оптимизации в работах Kaveh A. [16]–[19]. Некоторые проблемы периодических систем, в частности регулярных ферм, рассмотрены в [20]. Задачи нелинейных колебаний ферм решались в [21]–[23]. Нелинейные деформации и динамический отклик фермы кольцевой ферменной антенны численно изучены в [24], [25].

Значение первой (основной) частоты собственных колебаний является одной из главных динамических характеристик конструкции. Для этой частоты известны приближенные методы получения верхней и нижней оценок. Это методы, использующие значения парциальных частот, которые можно найти аналитически. Для регулярных конструкций возможно обобщение решений на произвольное число панелей фермы методом индукции [26], [27].

В настоящей работе предлагается схема статически определимой пространственной фермы призматического типа с пирамидальным куполом, и дается вывод формулы для расчета нижней границы первой собственной частоты для произвольного числа панелей. Спектр собственных частот анализируется численно.

• 2    Материалы и методы / Materials and Methods

  2.1    Схема фермы

Ферма в виде правильной шестигранной призмы высотой h ( n — 1) и шестигранной пирамиды купола высотой h /2 сверху содержит n s = 18 n + 3 стержней, включая шесть вертикальных опорных стоек и три горизонтальные опорные связи в углах основания, имитирующие сферический шарнир в узле A и цилиндрический шарнир в узле B (рис. 1, 2). Призма вписывается в цилиндр радиусом R .

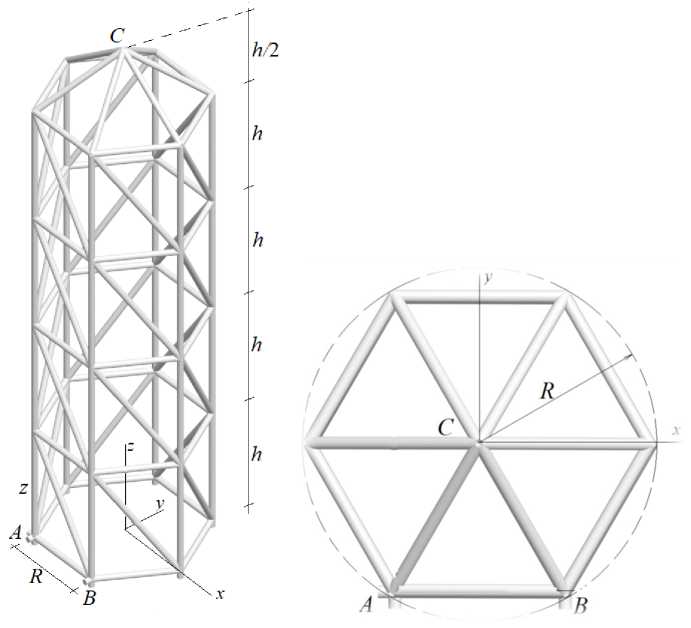
Рис. 1. - Схема фермы, п= 5

Рис. 2. – Купол конструкции

Fig. 1. - Truss scheme, n= 5

Fig. 2. – Dome construction

Раскосы в ферме имеют длину d = Rr ² + h² . Стержни конструкции соединены шарнирно. Для расчета усилий в стержнях в программу, написанную на языке символьной математики Maple [28], вводятся координаты узлов. Начало координат принято в основании на оси симметрии конструкции (рис. 3).

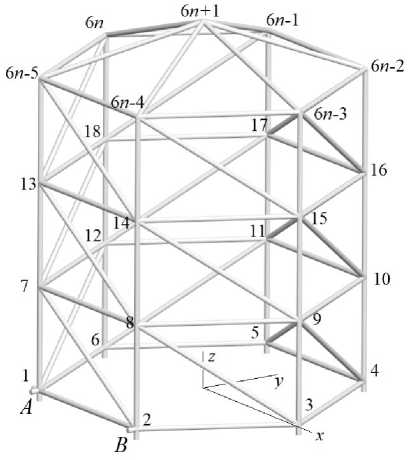
Рис. 3. - Номера узлов, п= 4 Fig. 3. - Node numbers, п= 4

Координаты внутренних узлов конструкции имеют вид:

x       = R cos(^i), y      = R sin(^i), z = (j — 1)h, i+6( j—1)                          i+6( j—1)                          i +6( j—1)

j = 1,.., n , i = 1,..,6, ф = 2 ^ /6.

Координата вершины C :

x = 0, y = 0, z = h ( n — 1/2). 6 n + 1            6 n + 1       ⁷ 6 n + 1

Конфигурация решетки вводится в программу с помощью специальных упорядоченных списков номеров концов соответствующих стержней, точно также, как задаются графы в дискретной математике. Стойки конструкции, например, кодируются следующими списками вершин:

^Ф i _{+ 6(} j _— 1) = ^[ i ^{+ 6(} j ^— 1), i ^{+ 6( j —} 1) ^{+ 6]} , i = ^1, .• ^{,6, j} = ^1," > ^{n —} 1.

Эти списки не ориентированы, выбор начала и конца стержня не влияет на решение. Стержни шестигранной пирамиды с вершиной в узле C кодируются аналогично:

^Ф 18 n _— 1_{2 +} i = ^[6( n ^— 1) ⁺ i ^,6 n ^{+ 1]} , i = ^1," > ⁶ -

2.2    Расчет усилий в стержнях

Для расчета жесткости конструкции по формуле Максвелла – Мора необходимы величины усилий в стержнях. В статически определимой системе усилия определяются из уравнений равновесия узлов в проекции на оси координат. Система уравнений записывается в матричном виде GS = Y, где G — матрица коэффициентов, состоящая из направляющих косинусов усилий, рассчитанных по координатам узлов и спискам номеров концов стержней Фi, i = 1,.., ns, S— вектор неизвестных усилий и реакций опор, Ψ — вектор нагрузок на узлы. На каждый узел фермы выделяется по три строчки матрицы Gи три соответствующих элемента вектора нагрузок. В элементы вектора нагрузок вида Ф3i, где i — номер узла, записываются нагрузки на этот узел в проекции на ось x. Элементы Ф3i_1 содержат проекции сил на ось у. Вертикальные нагрузки записываются в элементы Ф3i.

По значениям координат узлов и порядку соединений стержней в узлах вычисляются проекции единичных векторов усилий в уравнениях равновесия узлов на оси координат:

I . = (x _ x ) / I. , I . = (y _ y ) / I. , I . = (z _ z ) / I, i = 1,..., n , x , i            Ф- ,          Ф i ^,    y , i            Ф Ф i ^,     z , i            Ф- ,         Ф            i ^{,             ,     ,} s ^,

^,                        i ,1                   i ,2                        y ^,                        i ,1                  i ,2                           ^,                        i ,1                  i ,2

где l i = .^ i + l^ + l^ — длина стержня i . В число стержней включены опорные стержни в основании конструкции. Матрица коэффициентов уравнений равновесия в проекциях заполняется по строкам. Каждые три строки соответствуют уравнениям проекций на оси x, y и z соответственно:

G = l / l. G       = l / l., G . = l / l. ,

3 Ф i 1 _ 2, i         x , i г* 3 Ф i 1 _ 1 , i         y , i i"         3 Ф i 1 , i         z , i г*

G ’ = =-l . / I. , G„     = -l . / I. , G. .=-1 . / l ..

3 Ф _О_2, i           x , i      i*    3 Ф ₀_1, i           y , i      i*     3 Ф ₀, i           z , i      i

• i,2 ^{,                             ,}                                   i,2 ^,                         ^^,                                     i,2^{,                            ,}

2.3    Собственная частота колебаний

Здесь учтено, что проекции усилий, приложенных к разным концам одного стержня, имеют противоположные знаки.

Для расчета частот колебаний конструкции используется наиболее распространенная модель, в которой масса фермы сосредотачивается только в ее узлах равномерно по всей конструкции. Принимается, что у каждой массы две степени свободы. Колебания масс по вертикальной оси z не учитываются. Число степеней свободы рассматриваемой модели фермы K = 2(6 n + 1) .

Система дифференциальных уравнений динамики грузов имеет матричный вид: • *

M K U + D K U = 0 ,                             (1)

где U – вектор горизонтальных перемещений масс 1,..., K , D _K – матрица жесткости системы, M _K - матрица инерции, ^ — вектор ускорений. Матрица инерции пропорциональна единичной матрице M K = m I K , так как массы одинаковые. Матрица податливости B K , обратная к матрице жесткости D _K , определяется по формуле Максвелла-Мора:

n s b,, = у s(i)s(j)l /(EF ),                                  (2)

i, j             a a a a a=1

где 8^ i ) — усилие в стержне a от действия единичной силы в узле i, приложенной по направлению колебаний . Умножение векторного уравнения (1) слева на матрицу B _K с учетом замены U = _ ш ² U , соответствующей гармоническим колебаниям, сводит задачу к проблеме собственных чисел матрицы B K : B K U = A U , где А = 1 / ( mш ²) — собственное число матрицы ^B K , ш — собственная частота колебаний. Отсюда получается формула для вычисления частоты колебаний: ш = J 1 / ( mA ) .

Усилия 8⁽_a i ) в стержнях фермы, входящие в элементы матрицы B K , определяются из решения системы уравнений узлов фермы. В систему уравнений равновесия входят и реакции девяти опор.

Получить аналитические решения для фермы с произвольным числом панелей в общем случае можно только численно. Известны две оценки первой частоты: оценка снизу по формуле Донкерлея и сверху по методу Рэлея.

Нижняя оценка первой частоты колебаний получается по формуле Донкерлея:

K ш-2 = уШ

Di i=1

где ш _i — парциальная частота колебания массы m , расположенной в узле i . При вычислении парциальных частот ш _i уравнение (1) принимает скалярную форму:

mu. + du. = 0, i ii

где u i - перемещение массы, U i - вектор ускорений, d i - скалярный коэффициент жесткости ( i — номер массы). Частота колебаний груза ш . = ^ d i / m . Коэффициент жесткости, обратный коэффициенту податливости, определяется по формуле Максвелла – Мора:

n s2

6. = 1/ d. =Е S ⁽ i ) l /(EF ) .

i              i / -v \ а а ' ^v а

а = 1

Здесь обозначено S⁽_а¹ ) — усилия в приложенной к узлу i . Из (3) и (4) следует:

стержне с номером а от действия единичной силы,

K

—        -2

шп = > ш.

Di i=1

K 1

= m E = m d i=1 i

K

E 6 = m

Kⁿ s

EE 8^i ) l / ( EF ) = m S . / -/ / j у а у а ' а 2            n

Сечение вертикальных стоек у р

отличается от сечений F остальных стержней

^{K ns}       ( i ) ²

коэффициентом 7 > 1. Последовательный расчет сумм Sn =ЕЕ^а)) 1а / (EFL) при n = 2,3,4,... дает:

S.

S.

S

s

= (2144 R ³ + 65 c ³ + 1680 d ³ + 9996 h ³ / 7 )/ (12 R ² EF ),

= 16840 R ³ + 287 c ³ + 14880 d ³ + 193578 h ³ / 7)/ (36 R ² EF ),

= 32048 R ³ + 379 c ³ + 29520 d ³ + 659024 h ³ / 7 ) / (36 R ² EF ), = 17352 R ³ + 157 c ³ + 16320 d ³ + 552866 h ³ / 7 ) / (12 R ² EF ),...

где c = л] 4 R ² + h ² . В общем случае: Sn = ( C 1 R ³ + C 2 c ³ + C 3 d ³ + C 4 h ³ / 7 ) / (R ² EF ).

Для получения общих членов последовательностей коэффициентов в этих выражениях потребовалось рассчитать в аналитическом виде не менее десяти ферм. Для меньшей длины последовательности операторы Maple общие члены не находят. В результате получены следующие коэффициенты:

C ₁ C C C

= 2(300 n ² - 199 n + 2)/ 9,

= (92 n + 11)/36,

= 20(10 n + 1)( n - 1)/3,

= (1338 n ⁴ + 62 4n ³ - 3742 n ² + 1679 n + 204) / 18.

В результате нижняя оценка для первой частоты по Донкерлею принимает вид:

Ш D = ^R

EF

m(C 1 R ³ + C 2 c ³ + C 3 d ³ + C 4 h ³ / 7 )

.

• 3    Результаты и обсуждения / Results and Discussion

  3.1    Пример

Оценить погрешность полученного приближенного аналитического решения можно на примере. Кривые на рисунке 4 показывают изменение частоты u D в зависимости от числа панелей, вычисленной по формуле (5) и частоты ш 1 , полученной численно, как минимальная частота спектра собственных частот конструкции при h = 3м, R = 5 м, у = 1 . Масса грузов в узлах равна 500 кг. Модуль упругости стали, из которой изготовлены все стержни конструкции, принят равным E = 2,1 • 10 5 МПа, площадь поперечных сечений F = 9 см 2 . Первая частота ш 1 собственных колебаний фермы, полученная численно, и оценка u D Донкерлея (5) сближаются с увеличением числа панелей. Для уточнения степени полученных приближений вводится относительная погрешность e d =| u D — ш \ /ш 1 (рис. 5).

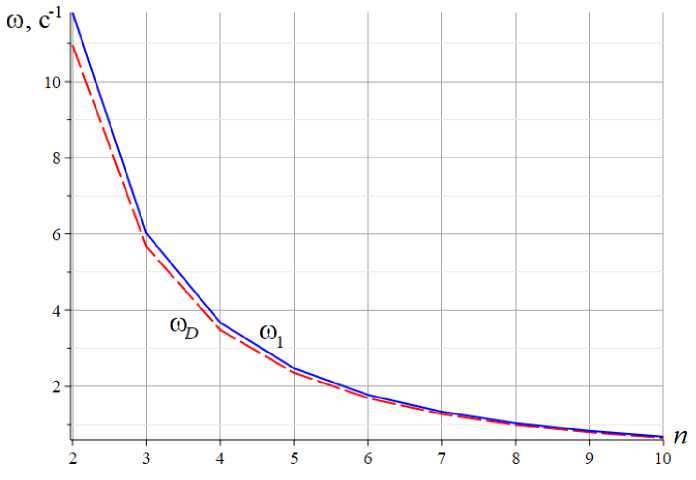
Рис. 4. – Первая частота колебаний, полученная двумя способами в зависимости от числа панелей

Fig. 4. - The first oscillation frequency obtained in two ways depending on the number of panels

В зависимости от числа панелей погрешность решения по Донкерлею меняется от 7%, при n = 2, до 4%. Замечено также, что степень приближения решения по Донкерлею несколько увеличивается при увеличении высоты конструкции.

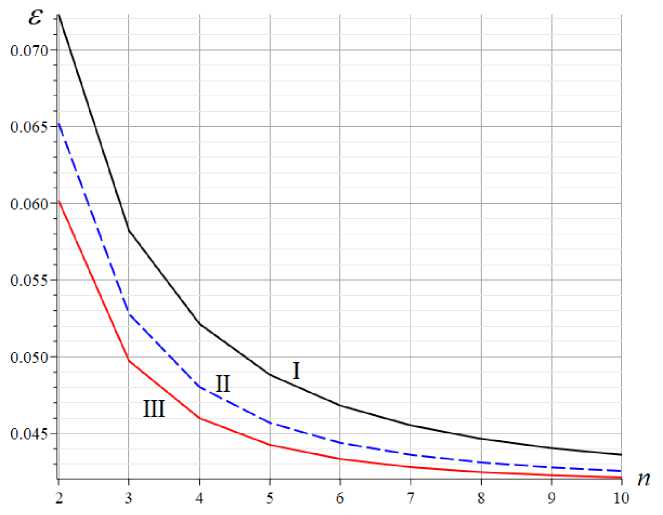
Рис. 5. – Относительная погрешность полученной оценки (5). I — h=3 м; II — h=4 м; III — h=5 м

Fig. 5. – Relative error of the obtained estimate (5). I — h=3 m; II — h=4 m; III — h=5 m

Анализ выведенной формулы показывает, что на значение первой частоты колебаний конструкции башенного типа при малых высотах h соотношение площадей сечения стержней практически не влияет (рис. 6). Эти же графики показывают, что частота колебаний с увеличением высоты панели падает.

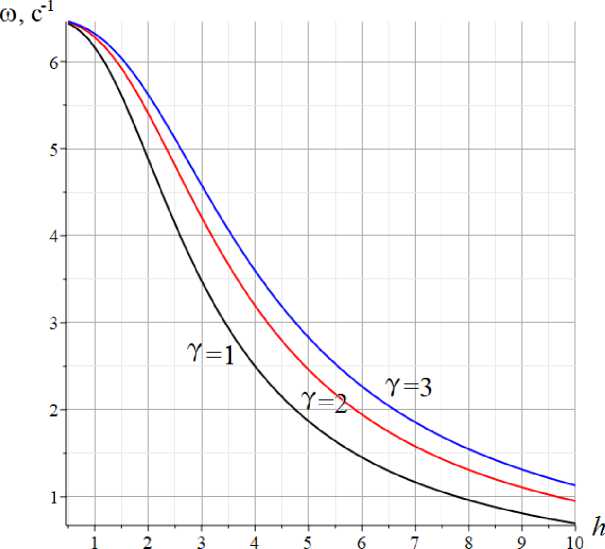
Рис. 6. – Зависимость основной частоты от высоты панели, n =4

Fig. 6. – The dependence of the fundamental frequency on the height of the panel, n =4

3.2    Спектр частот регулярных ферм

Значения высших частот собственных колебаний конструкции редко используются на практике. Как правило, при анализе резонансных явлений в расчет берутся несколько первых частот. Аналитически рассчитать эти величины в общем случае не удается, однако анализ распределения частот в спектре может выявить некоторые закономерности, полезные для практических расчетов, особенно для ферм с большим числом панелей. На рисунке 7 приведены результаты расчета частот тринадцати ферм различного порядка.

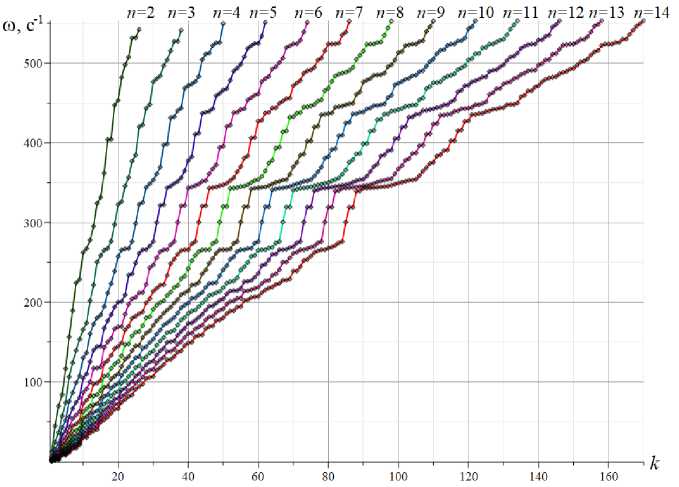
Рис. 7. Спектры частот регулярных ферм, h=3 m

Fig. 7. Frequency spectra of regular trusses, h=3 m

Каждая кривая соответствует спектру частот фермы заданного порядка, ординаты точек на ней — частоты, абсциссы — номера частот в спектре. Спектр фермы при n =2 содержит K = 2(6 n + 1) = 26 частот, в спектре фермы порядка n = 14 содержится 170 частот.

Здесь можно заметить некоторые частоты, одинаковые для всех ферм — спектральные константы [29], [30], а также частоты, имеющие один и тот же относительный номер в спектрах ферм различного порядка и лежащие на кривых, стремящихся к некоторому постоянному значению (спектральные изолинии) (рис. 8).

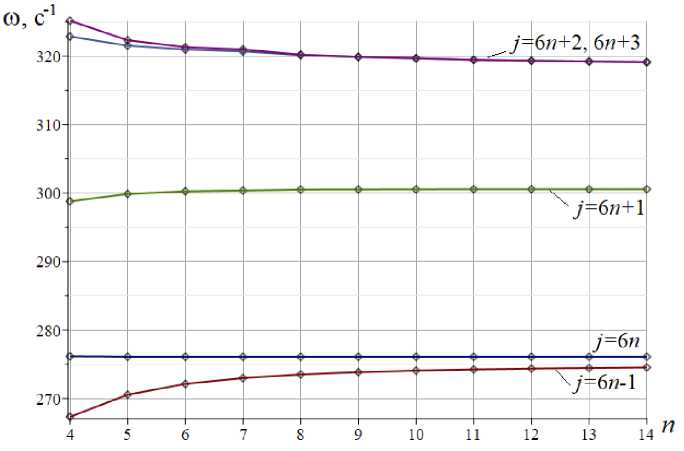
Рис. 8. – Спектральные изолинии и спектральная константа

Fig. 8. – Spectral isolines and spectral constant

На рисунке 8 параметр j — номер частоты в спектре (индекс кривой). Например, на кривой j = 6n + 1 первая точка — это частота с номером j = 6 ■ 4 + 1 = 25 в упорядоченном спектре частот фермы порядка n=4, следующая точка — частота с номером j = 6 ■ 5 + 1 = 31 в спектре фермы порядка 5 и т. д. Кривая j = 6n — это спектральная константа. Начиная с фермы некоторого порядка, соответствующие частоты не меняются (в пределах погрешности вычислений). Серия расчетов показала, что значение номера частоты в спектральной константе (здесь это индекс 6n) не зависит от порядка фермы. Значение же соответствующей частоты меняется при изменении размеров конструкции. Следует также отметить, что и высшая частота колебаний всех ферм рассмотренного семейства почти не меняется. Точки высших частот на рисунке 7 также образуют изолинию с индексом j = K, стремящуюся к некоторой константе снизу.

Выявление закономерностей распределения частот в спектрах регулярных систем вызвано не только теоретическим интересом. Для практических расчетов реальных конструкций, в которых возможны резонансные явления на высших частотах, важно знать границы изменения собственных частот и области сгущения частот, из которых желательно вывести спектр частот проектируемой конструкции.

Предложена схема статически определимой фермы пространственной осесимметричной конструкции башенного типа. Ферма имеет форму правильной шестигранной призмы с произвольным числом панелей по высоте. Такая конструкция может быть использована как опора или ограждающее сооружение. Ферма внешне статически неопределима. Реакции девяти опорных стержней можно найти только из решения совместной системы уравнений равновесия всех узлов в проекциях на оси координат одновременно с усилиями в стержнях. Но в настоящей работе решена более сложная задача. С достаточной степенью точности найдена аналитическая зависимость первой частоты собственных колебаний от размеров фермы и числа панелей. Это дает возможность применять полученную формулу для широкого класса конструкций предложенного типа. Формула практична. Без какого-либо ущерба для точности ее можно использовать при весьма большом числе панелей в конструкции, то есть именно в тех случаях, где требуются значительные вычислительные ресурсы и наиболее вероятно накопление ошибок в численных расчетах.

• 4    Заключение / Conclusions

Основные результаты работы:

• 1.    Предложена схема статически определимой фермы пространственной осесимметричной конструкции башенного типа с формой правильной шестигранной призмы и с произвольным числом панелей по высоте.

• 2.    Выведена аналитическая зависимость первой частоты собственных колебаний от размеров фермы и числа панелей.

• 3.    В спектрах собственных частот семейства ферм различного порядка обнаружены упорядоченные изолинии, выявляющие область сгущения высших частот и спектральные константы.

• 5 Благодарности / Acknowledgements

  Работа выполнена при финансовой поддержке РНФ 22-21-00473.