Модель сигнала обратного рассеяния для Иркутского радара некогерентного рассеяния

Одним из наиболее информативных инструментов наземной диагностики ионосферы над Сибирским регионом является Иркутский радар некогерентного рассеяния (ИРНР). История ИРНР началась в 1993 г., когда радиолокационная станция «Днепр» была переоборудована для выполнения научных задач. К 2014 г. была проведена глубокая модернизация приемного, регистрирующего, обрабатывающего и управляющего оборудования радара, что значительно увеличило его диагностические возможности [Potekhin et al., 2009; Медведев,

2014] . Модернизация не проводилась только на антенной системе, представляюшей собой H-секто-риальный рупор, который запитывается волноводнощелевой системой с ребристо-замедляющей структурой [Жеребцов и др., 2002] . Такая система позволяет излучать сигнал одной строго линейной поляризации в диапазоне рабочих частот 152–162 МГц, что не является вполне традиционным для метода НР и создает дополнительные сложности при определении параметров ионосферной плазмы.

Метод некогерентного рассеяния (НР) заключается в регистрации и последующей обработке обратного сигнала, рассеянного в среде при излучении заданной последовательности коротких импульсов. В отличие от традиционной радиолокации, где предметом исследования является дальность до сосредоточенного объекта, радар НР изучает ионосферу — пространственно-распределенный объект, охватывающий практически всю область видимости радара. Поэтому при обработке сигнала необходимо учитывать пространственно-временную конфигурацию рассеяния (рис. 1). Исследование статистических характеристик сигнала обратного рассеяния позволяет получить информацию о физическом состоянии плазмы ионосферы: высотное распределение концентрации, ионных и электронных температур, ионного дрейфа и т. д.

Физически сигнал обратного рассеяния формируется в результате интерференции сигналов, рассеянных на тепловых флуктуациях диэлектрической проницаемости плазмы. Такие флуктуации принято считать стохастическими, а распределение тепловых скоростей электронов — максвелловским. На основе этих допущений построена теория метода НР [Evans, 1969] , а знание функции распределения скоростей электронов позволяет аналитически получить выражение для спектра рассеяния сигнала в плазме [Шеффилд, 1978] . Однако в действительности движения электронов ионосферной плазмы могут не быть полностью независимыми, т. е. их траектории частично коррелируют, при этом масштабы корреляции зависят от соотношения длины волны радара и радиуса Дебая, ионных и электронных температур, а также от внешнего магнитного поля ионосферной плазмы. Существуют так называемые «коллективные эффекты» — проявления пространственной и временной корреляции между частицами ионосферной плазмы, которые могут искажать форму спектра сигнала обратного рассеяния когерентной составляющей, увеличивая систематическую погрешность метода. Несмотря на это, сложности, возникающие в результате таких коллективных эффектов и отраженные в доплеровском спектре «не вполне некогерентного рассеяния», могут дать большое количество дополнительной информации об

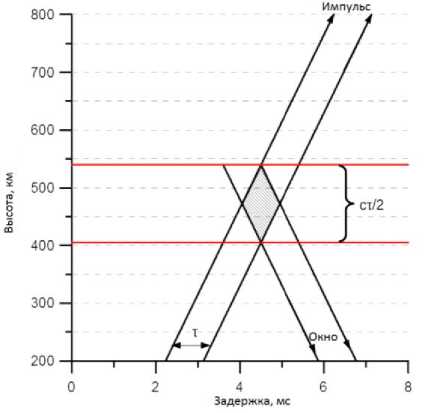
Рис. 1. Пространственно-временная конфигурация рассеяния импульса длительностью τ ионосфере при наличии корректной модели прямой задачи [Kudeki, Milla, 2012].

Ввиду случайного характера тепловых флуктуаций плазмы спектр или автокорреляционную функцию (АКФ) принятого сигнала необходимо усреднить в промежутке времени, в течение которого ионосферу принято считать неизменной. На практике для получения спектра сигнала с приемлемой дисперсией необходимо усреднение (в зависимости от отношения сигнал/шум) более 2000 реализаций (циклов излучение—прием сигнала). Для ИРНР длительность зондирующего импульса составляет от 200 до 900 мкс, а время регистрации сигнала — около 8 мс, что соответствует дальности 1200 км. При частоте повторения импульсов 24.4 Гц и коэффициенте заполняемости ~20 % требуется около 5 мин, чтобы накопить 3–4 тысячи реализаций. Как видно из рис. 1, пространственное разрешение восстанавливаемых профилей определяется длительностью излученного импульса.

Главная цель представленного исследования — разработка алгоритма поиска и устранения систематических погрешностей метода НР. Алгоритм должен учитывать конструктивные особенности ИРНР, а именно — наличие только одной линейной поляризации сигнала. В основе предложенного алгоритма лежит математическая модель сигнала обратного рассеяния, которая уже применялась для исследования возможности применения кодовых импульсных последовательностей на ИРНР для получения профиля электронной концентрации [Alsatkin et al., 2009] . В данной работе основное внимание уделено простой импульсной форме излученного сигнала — только в этом режиме ИРНР на данный момент возможно восстановление профилей ионных и электронных температур. Предложенный нами метод можно развивать применительно к оценке других параметров ионосферной плазмы: например ионного состава, направления и величины скоростей дрейфа и электрических полей плазмы. Он также перспективен с точки зрения исследований неоднородностей ионосферы, поскольку вызываемые ими коллективные эффекты достаточно просто интерпретировать в модели сигнала обратного рассеяния.

ПОСТАНОВКА ЗАДАЧИ

Одна из наиболее актуальных задач для научного коллектива ИРНР — корректное определение ионных и электронных температур ионосферной плазмы. Разработка методики восстановления температур для ИРНР имеет сложности, связанные, в первую очередь, с конструкцией антенны радара. Наличие только одной линейной поляризации приводит к невозможности восстановления непрерывного профиля температур из-за характерных замираний мощности сигнала, возникающих вследствие эффекта Фарадея. При прохождении линейно поляризованного сигнала в среде вдоль магнитного поля плоскость поляризации испытывает вращение на всем пути распространения сигнала и скорость ее вращения в первом приближении зависит от электронной концентрации. С одной стороны, это позволяет восстановить профиль электронной концентрации без калибровки по данным ионозондов, как на радарах НР с круговой поляризацией. С другой стороны, когда плоскость поляризации детектируемого сигнала перпендикулярна поляризационному фильтру радара, в профиле мощности возникают замирания, характеризующиеся еще более низким отношением сигнал/шум.

В режиме ионосферных наблюдений ИРНР излучает последовательно два импульса разной частоты: первый, длительностью 700 мкс, является ампли-тудно-модулированным, второй, длительностью 200 мкс, — фазоманипулированным (код Баркера). С 2013 г. на ИРНР введен режим последовательного излучения и приема двух импульсов длительностью 700 и 900 мкс. Применив к полученным данным метод эффективных вычитаний [Berngardt et al., 2013], можно добиться лучшего пространственного разрешения измеряемых параметров. Сигнал от каждого импульса принимается независимыми каналами — узкополосным (700 и 900 мкс) и широкополосным (200 мкс). В узкополосном канале исследуется сигнал с хорошим частотным разрешением, что позволяет восстанавливать физические параметры, связанные с формой ионно-акустической линии спектра. Частотное разрешение определяется длительностью приемного окна, которое, как правило, выбирается равным длительности импульса. Такая оконная обработка позволяет проводить оценку АКФ сигнала, достаточную для определения ионных и электронных температур. Точность оценки параметров АКФ сигнала зависит от отношения сигнал/шум и систематических погрешностей, учет которых возможен только при наличии достоверной физической модели рассеяния и приема сигнала антенной.

Широкополосный канал дает информацию о мощности сигнала с высоким пространственным разрешением 6 км, что позволяет восстанавливать профиль электронной концентрации по фазе фарадеевских замираний. Метод определения концентрации для ИРНР описан в работе [Ratovsky et al., 2017] . В процессе восстановления электронной концентрации определяется модельный профиль замираний (рис. 2).

Другая важная особенность ИРНР заключается в длине волны радара ~2 м. Как известно в теории НР, неоднородности ионосферы с характерным масштабом, сопоставимым с длиной волны радара, могут возбуждать когерентную составляющую в сигнале обратного рассеяния. Как правило, радары НР имеют длину волны намного меньше 1 м, что гораздо меньше минимального масштаба неоднородностей, связанных, например, с F-рассеянием. Методика идентификации среднеширотных неоднородностей для диапазона длин волн ИРНР и оценка связанных с ними систематических погрешностей представляют предмет будущих исследований. Основной целью данной работы является устранение вызванной фарадеевскими замираниями мощности сигнала погрешности оценки температур ионосферной плазмы.

Для решения данной задачи необходимо решить три подзадачи. Первая подзадача состоит в том, чтобы получить радиолокационное уравнение, связывающее спектральные или корреляционные характеристики сигнала, регистрируемого приемником, с соответствующими характеристиками флуктуаций плазмы. Вывод данного уравнения в различных приближениях приведен в работах [Berngardt, Po-tekhin, 2000; Shpynev, 2004] . Вторая подзадача заключается в построении метода устойчивого решения радиолокационного уравнения, которое, как и множество других задач геофизики, представляет собой обратную задачу, которая математически некорректна. В работе [Holt et al., 1992] предложен метод оптимального анализа полного профиля (OASIS — optimal analysis of signals from incoherent scatter) — алгоритма подгонки высотных профилей искомых параметров (концентрации, температур, ионного состава) под экспериментальные значения АКФ методом наименьших квадратов. Данный метод успешно применяется на радарах НР Миллстоун Хилл и Джика-марка (например [Hysell et al., 2008] ). Другой подход построен на статистической теории обратных задач [Tarantola, 1987; Lehtinen, 1986] и интерпретирует данные НР как случайные гауссовы переменные, а для решения радиолокационного уравнения применяется теорема Байеса. Решение третьей подзадачи позволяет связать физические параметры плазмы (например температуры) и спектра или АКФ флуктуаций плазмы. Решение данной задачи тесно связано с решением второй подзадачи и определяет, насколько физическая модель спектра рассеянного сигнала соответствует наблюдаемым экспериментальным значениям.

ПОСТРОЕНИЕ РАДИОЛОКАЦИОННОГО УРАВНЕНИЯ

Предлагаемая нами модель сигнала обратного рассеяния интерпретирует среду как равномерно распределенный по высоте набор «рассеивателей», каждый из которых отражает сигнал со случайной фазой (согласно равномерному распределению), но с амплитудой, пропорциональной амплитуде спектра флуктуаций плазмы на заданной частоте. В таком приближении сигнал обратного рассеяния представляет собой интерференцию сигналов, отраженных от этих рассеивателей. В качестве модели спектра рассеяния используется выражение из работы [Шеффилд, 1978] для низкотемпературной бесстолкновительной плазмы с ионами одного сорта O⁺.

Мощность принимаемого сигнала в первую очередь зависит от концентрации электронов и ориентации плоскости поляризации относительно поляризационного фильтра радара. В прямую задачу ее можно ввести как амплитудную модуляцию сигнала обратного рассеяния с помощью одного из экспериментально полученных профилей мощности.

Для решения поставленной задачи мы предложили дискретную математическую модель формирования рассеянного сигнала. Модель сигнала обратного рассеяния можно представить в виде

N

• 5 ( t ) = £ F ( hQ I h - ct К S e ^{( m} nh t ⁺ 2 k^nhh ^{+ ф nh} ) ,    (1)

• h           V      ² ) n =0

  

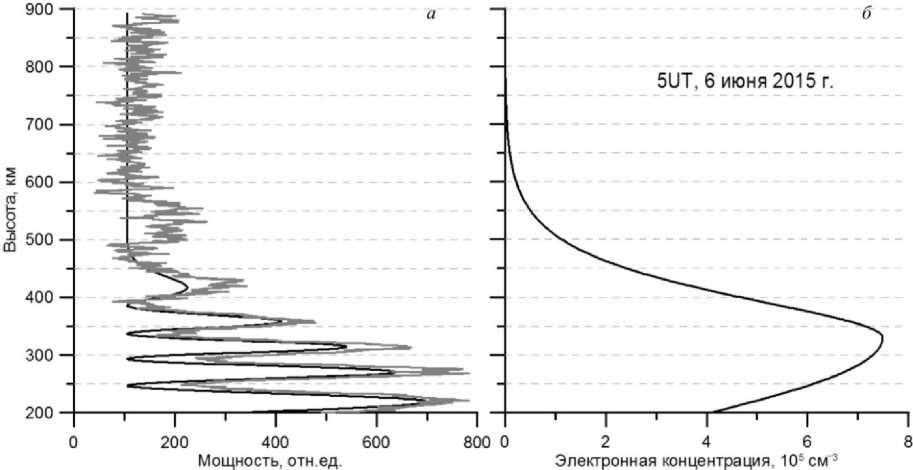
  Рис. 2. Сравнение экспериментального профиля мощности широкополосного канала и модельного профиля замираний мощности ( а ) и восстановленный профиль концентрации ( б )

  
  

где F ( h ) — профиль фарадеевских замираний, S nh , ω nh , k_nh — амплитуда, частота и волновое число спектра рассеяния плазмы для n -го иона и высоты h , φ nh — случайная фаза рассеяния, Q — огибающая зондирующего импульса. Приведенное выражение получено в приближении импульсной характеристики антенноприемного тракта радара в виде дельта-функции (для активных экспериментов ИРНР частотная полоса приемника составляет 125 кГц), что упрощает интеграл Дюамеля. Функция s ( t ) представляет модель квадратурного сигнала, принятого гетеродинным приемником. Форму излученного импульса можно считать идеальным прямоугольником.

С учетом технических особенностей ИРНР и специфики решаемой задачи на основе представленной модели можно построить радиолокационное уравнение для АКФ сигнала обратного рассеяния. Сравнение полученного уравнения и традиционного уравнения теории НР [Farley et al., 1969] позволит сделать вывод о справедливости предлагаемой нами интерпретации рассеяния. Для стационарного случайного процесса АКФ сигнала для оконной функции o ( t ) имеет вид

R ( ^т ) = Z ⁵ ( t ) o ( t ) ⁵ * ( t - ^т ) o (t - ^t). (2) t

Выражение (2) представляет АКФ отдельной реализации сигнала и пока не связывает ее с АКФ флуктуаций плазмы. Однако, используя описанные ниже свойства суммы и характер распределения фазы φ, это выражение можно упростить (Приложение), получив в качестве составляющего уравнения обратное преобразование Фурье спектра мощности рассеяния сигнала в плазме. Согласно теореме Винера—Хинчина, это составляющая и есть АКФ рассеянного сигнала.

При усреднении полученного выражения три последних слагаемых обратятся в нуль, если считать, что фазы φnh имеют равномерное распределение. Тогда усредненная АКФ реализаций сигнала обратного рассеяния примет вид

(R ^{( т}, h )} =

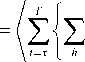
N

F ² ( h ) w (t, t , h , h ) £ S n,_h e ^{2 / m} nh n =0

^T_ r                                     )\

• ⁼ \Ё ] Е [ F ( h ) w ( т, t , h , h ) R 0 (т, h ) ] f ),

• \ t =т I h                                                     J,

  где R 0 — обратное преобразование Фурье спектра флуктуаций плазмы (АКФ). Полученное радиолокационное уравнение согласуется с уравнением, получаемым в теории НР [Farley et al., 1969] , и при этом позволяет учитывать в прямой задаче эффект Фарадея для радара НР с одной линейной поляризацией. Принятые при выводе данного уравнения приближения обусловлены исключительно практическими соображениями, поскольку неучет импульсной характеристики приемника вносит в эксперимент очевидно гораздо меньшую погрешность, чем эффект Фарадея.

РЕШЕНИЕРАДИОЛОКАЦИОННОГО УРАВНЕНИЯ

Полученное радиолокационное уравнение можно разложить на множество независимых по τ систем линейных уравнений. Главная сложность состоит в том, что эти системы уравнений являются неполными и плохо согласованными. Это обусловливает необходимость регуляризации предполагаемых решений и привлечения максимально возможного объема априорных данных и данных других измерений. Такой подход реализован в методах, предложенных в [Lehtinen, 1986; Holt et al., 1992]. Основным его недостатком является то, что при несоответствии физической модели реальным явлениям, имеющим место в ионосфере, возникающая систематическая погрешность не будет учтена. Кроме того, дисперсия сигнала довольно быстро увеличивается с высотой, поскольку его мощность при моностатическом позиционировании обратно пропорциональна r2 (r — дальность), а время интегрирования реализаций ограничено временем стационарности ионосферы; это может привести к тому, что в анализ полного профиля будут вовлечены дальности, для которых сигнал уже не несет какой-либо физической информации. Поэтому равноценную значимость имеют и устойчивый метод решения обратной задачи, и поиск систематических погрешностей, не учитываемых ранее в прямой задаче. В связи с этим было предложено контролируемое упрощение радиолокационного уравнения, позволяющее быстро оценить решение в первом приближении:

G e = a ²

G i = a ²

R 0 ( ^т ) =

R (т) W (т),

где

T

W (т )=Zx t=т

X

F 2 ( h ) Q f h l - Ct J Q f h 2 - c^ + C T ] o ( t ) o ( t - ^т )

— весовая функция, которую в теории НР также называют функцией неопределенности. Функция W ( т ) монотонно убывает в положительной области т, имеет максимум при τ=0 и обращается в нуль при τ, равном длительности зондирующего импульса. Этот подход перспективен с точки зрения поиска источников аддитивного рассеяния применительно к экспериментальным данным.

СВЯЗЬ ТЕМПЕРАТУР

СО СПЕКТРОМ РАССЕЯНИЯ

Аналитическое описание спектра флуктуации диэлектрической проницаемости плазмы приведено в [Шеффилд, 1978] :

S ( k s , ® ) = ^1 k

s

G e —

f e0

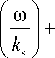
2π Z k _s

G i

, (5)

где k s =4π f 0 / c — волновое число, f 0 — рабочая частота

Г V ²

expl--2 f a радара, Z — заряд иона; fe (v ) =--------

( п a ² ) ²

и

f0о (v ) =

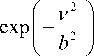
( n b ² ) ²

распределения скоростей

электронов и ионов в термодинамическом равновесии (распределение Максвелла); a =(2 k b T e / m e )^1/2 и b =(2 k b T i / m i )^1/2 — тепловые скорости электронов и ионов ( k _b — постоянная Больцмана);

x _e

1 - 2 x _e e - ^{x e} J pe p dp - г n ^1/2 x _e e - ^x‘

1 - 2 x i e -'²J pe ^{p 2} dp - i n ^1/2 x i e - ^{x 2}

f           0

интегралы Гордеева для незамагниченной плазмы; α=1/( k λ D ), x e =ω/( ka ), x i =ω/( kb ), ε=1+ G e + G i и λ D — радиус Дебая.

Решение данной подзадачи можно проводить путем фитирования полученных спектров аналитическими спектрами флуктуации плазмы, с которыми однозначно связаны ее параметры. Однако такой подход с точки зрения объемов необходимых вычислений не оправдан. Достаточно оценить лишь несколько характерных значений АКФ (задержки первого нуля и первого минимума действительной части АКФ, а также амплитуду ее первого минимума) [Рогожкин, 1979] и построить регрессию температур на эти параметры. Это позволяет получить простые эмпирические формулы для быстрой и точной оценки температур.

Построение регрессии осуществлялось численно с помощью метода наименьших квадратов. Для вычислений использовался итеративный алгоритм Гаусса—Ньютона. На каждой итерации приближение искомой функции находится в виде

f ( β , x )= f ( β 0 , x )+ J 0 ( β – β 0 ),                           (6)

где J 0 — Якобиан функции f .

Итеративная оценка вектора β проводится в уравнении:

в _{у +} 1 = e _y + ( J T J 0 ) - 1 J T e,                           (7)

где e — текущий вектор остатков для j -й итерации.

В результате построения регрессии были получены формулы для определения T _e и отношения T r = T e / T i :

T « 1.9 - 108^ + 1.12 - 10 5 x e2 τ₀

x — - 2.2 - 10 8 1- + 2.03 - 10 5 ¹ - 24;

τ 0              τ min                τ ^min

T r - 13.8 A 1 - 0.04 A min + 0.5,                  (8)

где τ₀, τ_min, A _min — соответственно, задержка первого нуля, задержка и амплитуда первого минимума действительной части АКФ. Поскольку ИРНР излучает и принимает сигнал в диапазоне частот 154–162 МГц, важно ввести в регрессию погонные параметры, учитывающие длину волны. В выражении (5) длина волны входит как множитель 1/Х ( k s = 4лД) и как параметр нелинейных функций f e0 и f i0 , однако, как видно на рис. 3, этой нелинейной зависимостью можно пренебречь. Поэтому параметры АКФ должны быть нормированы на длину волны, равную 2 м.

λ t0 = t0 ^°,

λ

‘ min min λ ,

где λ₀=2 м, λ — текущая длина волны, t ′₀ и t ′_min — задержки первого нуля и первого минимума действительной части АКФ сигнала.

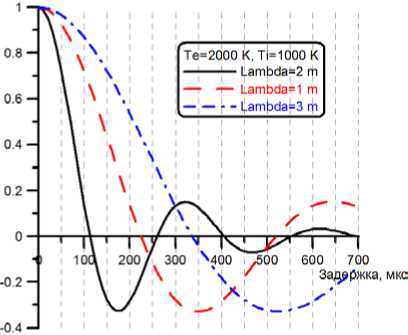
Рис. 3. АКФ рассеяния для длин волн 1, 2, 3 м

Оценка погрешности полученной регрессии показана на рис. 4. Максимальное отклонение не превышает 10 %, что при экспериментальном соотношении сиг-нал/шум ^ 1 можно считать приемлемым. Ошибка регрессии превышает 5 % для значений ионных и электронных температур, которые фактически не являются характерными для ионосферной плазмы в наблюдаемом ИРНР диапазоне высот.

Проверку построенного решения обратной задачи можно осуществить путем моделирования процесса формирования сигнала обратного рассеяния.

МОДЕЛИРОВАНИЕ

Моделирование формирования сигнала обратного рассеяния проводилось в соответствии с постановкой прямой задачи. Далее необходимо накопить несколько тысяч реализаций квадратур сигнала, чтобы усреднить их автокорреляционные функции. Такая задача требует большой вычислительной мощности, поэтому для вычислений был использован вычислительный кластер «Академик В.М. Матросов» []. Распараллеливание вычислений позволило добиться многократного ускорения работы модели.

После усреднения полученных АКФ можно применить уравнения (4) и (8) и сравнить значения заданных и восстановленных температур. На входе модели задавались линейные градиенты ионных и электронных температур, а также фарадеевские вариации мощности сигнала, экспериментально полученные на ИРНР. Неучет замираний мощности сигнала при решении радиолокационного уравнения приводит к тому, что восстанавливаемые профили температур абсолютно не соответствуют ожидаемым. На рис. 5 сравниваются входные данные модели и восстановленные профили температур с учетом профиля замираний мощности сигнала. Максимальные ошибки ~10 % для T e и ~20 % для T i можно считать приемлемыми для накопленной статистики ~2000 реализаций.

Чтобы проверить, устраняется ли систематическая погрешность от замираний мощности сигнала, было накоплено ~100 000 независимых реализаций, при этом для каждых 300 реализаций ядро случайной последовательности изменялось. Затем АКФ смоделированного сигнала были усреднены по 2000 реализаций. При тех же входных параметрах модели

(см. рис. 6) восстановленные температуры повторяли заданный ход с относительно постоянной дисперсией. На рис. 6 представлены профили характерных значений АКФ моделируемого сигнала для длительности импульса 700 мкс: a , б , в — соответственно, задержки первого нуля и первого минимума, а также амплитуда первого минимума действительной части АКФ до ее обращения уравнением (4); г , д , е — соответственно, задержки первого нуля и первого минимума, а также амплитуда первого минимума действительной части АКФ после ее обращения уравнением (4). Как видно из рис. 6, б , в , заложенный фарадеевский профиль мощности искажает форму АКФ, внося характерные провалы в значения этих параметров. Однако и амплитуда функции неопределенности имеет похожие особенности, и в результате применения уравнения (8) восстанавливается градиент параметров, соответствующих заданным температурам (рис. 6, д , е ). Слабое отличие поведения первого нуля АКФ (рис. 6, а , б ) косвенно говорит о справедливости принятого приближения, которое подразумевает мультипликативный характер решения обратной задачи.

АПРОБАЦИЯ РАЗРАБОТАННОЙ МЕТОДИКИ ВОССТАНОВЛЕНИЯ ТЕМПЕРАТУР

НА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ИРНР

В предложенном нами алгоритме восстановления температур не заложена регуляризация, поэтому получаемое экспериментально решение не является устойчивым и не позволяет корректно восстанавливать температуры по данным ИРНР в ряде обстоятельств. Во-первых, при наличии в исследуемой ионосфере мелкомасштабных неоднородностей сигнал обратного рассеяния может содержать сильные помехи, искажающие форму АКФ сигнала. Второе обстоятельство — пониженное отношение сиг-нал/шум при малом количестве замираний мощности, что наблюдается, например, при пониженной концентрации. В этом случае необходимое время интегрирования реализаций сигнала может превысить время стационарности ионосферы.

Проверка разработанной методики была проведена на экспериментальных данных ИРНР для летних дней и спокойной геомагнитной обстановки, когда количество фарадеевских замираний достаточно велико, а их ширина меньше длительности импульса, что приводит к относительно слабому искажению полученных профилей температур вследствие эффекта Фарадея. Восстановленные значения температур в сравнении с концентрацией электронов для 11–15 июня 2015 г. показаны на рис. 7. Суточный ход полученных температур вполне соответствует ожидаемому ходу.

На рис. 8 представлено сравнение временного хода ионных температур по данным ИРНР и хода температур нейтралов по данным наблюдений интерферометра Фабри — Перо, установленного в с. Торы [Васильев и др., 2017] .

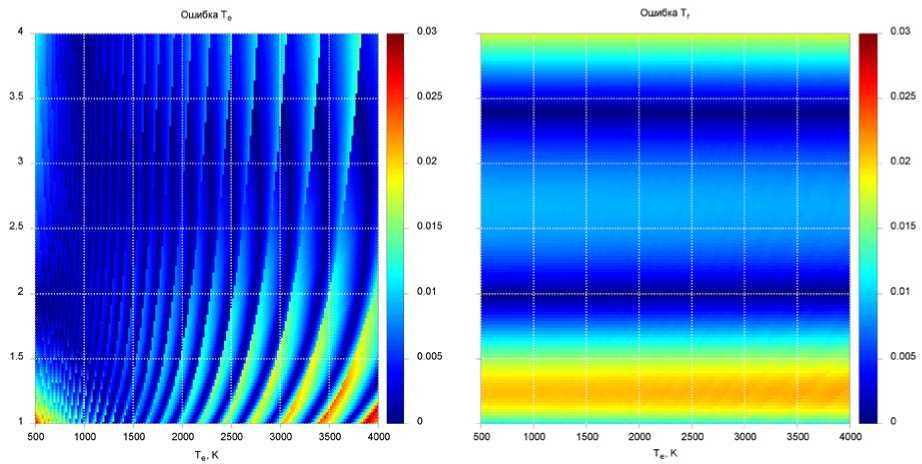
Рис. 4. Отклонение построенной регрессии от модели спектра рассеяния, уравнение (8)

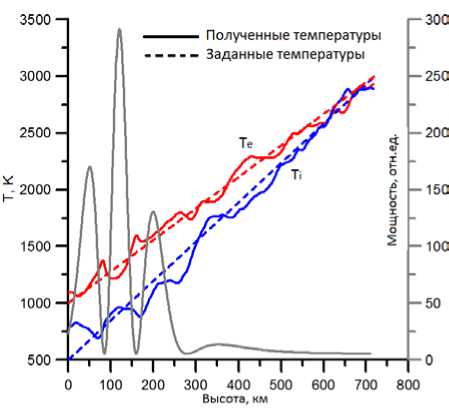
Рис. 5. Сравнение заданных и восстановленных моделью температур для характерного профиля фарадеевских вариаций мощности сигнала, регистрируемого на ИРНР

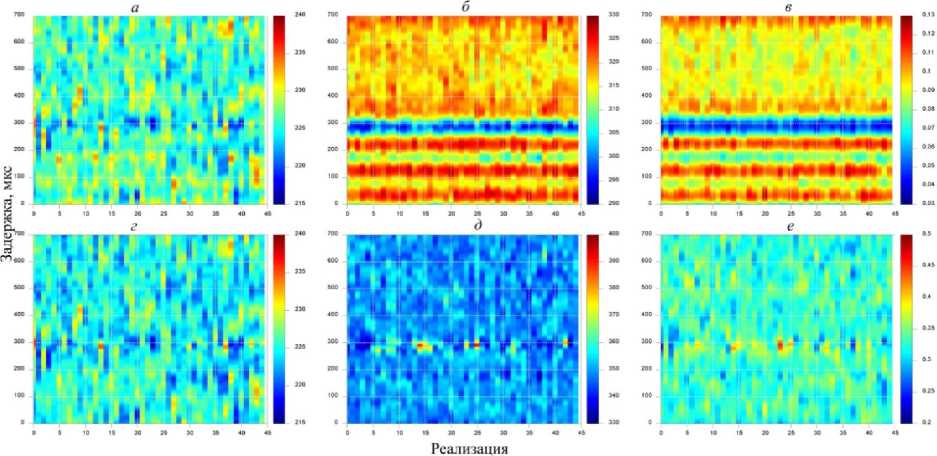
Рис. 6. Т о (< R (т)>) ( a ); т_шш (< R (т)>) ( б ); A _Ш1П (< R (т)>) ( в ); Т о ( R о (т)) ( г ); т_шш ( R о (т)) ( д ); A _Ш1П ( R о (т)) ( е )

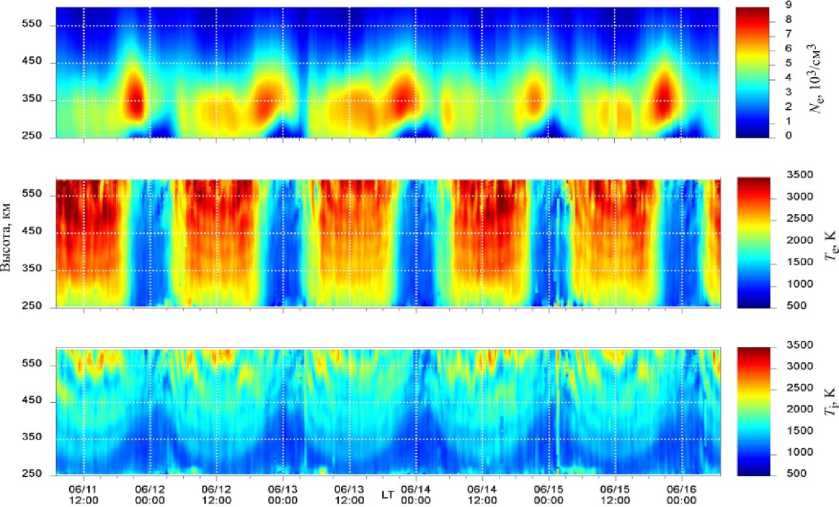
Рис. 7. Концентрация электронов, электронные и ионные температуры по данным ИРНР 11–15 июня 2015 г.

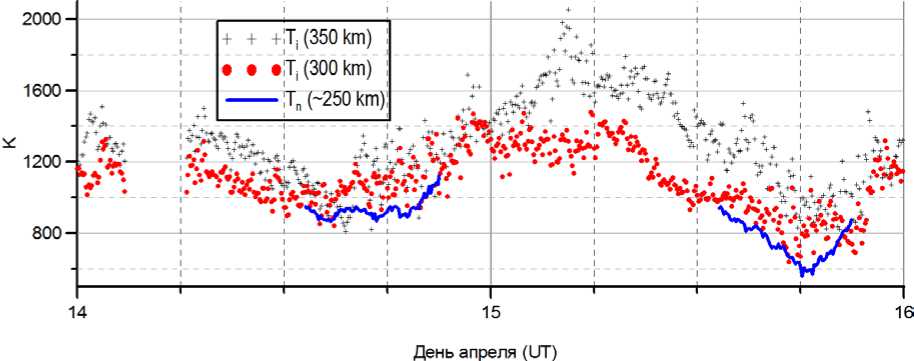
Рис. 8. Сравнение ионных температур, полученных по данным ИРНР, и температур нейтралов, полученных по данным наблюдений интерферометра Фабри — Перо

Таким образом, исключив вероятные технические ошибки обработки данных, можно поставить задачу поиска других систематических погрешностей. В результате анализа обработанных данных были построены гипотезы о существовании нескольких систематических погрешностей, не учитываемых ранее.

• 1.    Весовая функция построена некорректно вследствие неопределенности входных данных, т. е. профиля мощности широкополосного сигнала. Из-за слабой энергетики сигнала (длительность импульса всего 200 мкс, что соответствует диапазону высот 30 км) на высотах выше 400 км перестают различаться фарадеевские вариации мощности сигнала, которые, безусловно, вносят свой вклад в АКФ. Кроме того, уровень провалов мощности сигнала, строго говоря, может быть не нулевым и не постоянным по высоте.

• 2.    Ошибка приближения, используемого для получения уравнения (4), возникает при сильном градиенте температур. Однако на основе описанной модели была протестирована работа алгоритма для различ-

• ных градиентов температур. В каждом случае были восстановлены правильные значения температур.

• 3.    Другим важным свойством является характер функции неопределенности при однопозиционном зондировании с учетом эффекта Фарадея, что проиллюстрировано на рис. 9, 10. При оконной обработке сигнала центр засвеченного объема ионосферы приходится на начало выбранного окна, так как вклад в результирующую АКФ вносит сигнал не только в текущем окне, но и в предыдущем. Для сравнения были выбраны высоты 300 и 350 км для 4 и 15 UT 15 апреля 2016 г.

Как видно из рис. 9, главный вклад в АКФ вносит сигнал с высот, значительно ниже высоты, к которой привязано окно. При усреднении АКФ, энергетика которых существенно отличается, решающий вес имеет АКФ с наибольшей энергетикой. В результате полученные значения температур соответствуют не высоте выбранного окна, а «центру масс» весовой функции, который может быть как ниже выбранной

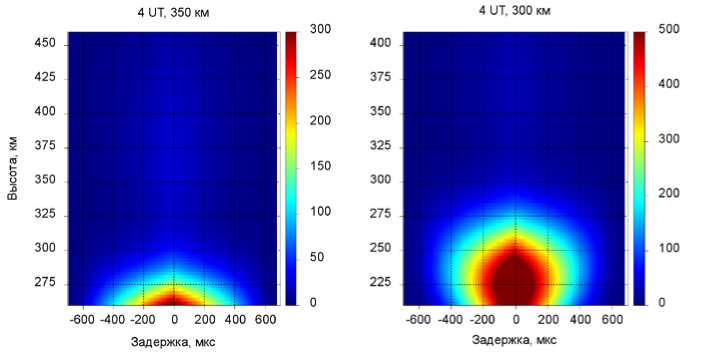
Рис. 9. Амплитуда функции неопределенности для окон на высотах 300 и 350 км для 4 UT 15 апреля 2016 г.

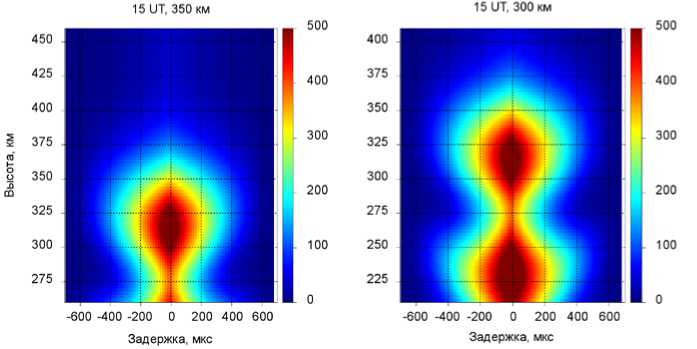
Рис. 10. Амплитуда функции неопределенности для окон на высотах 300 и 350 км для 15 UT 15 апреля 2016 г.

высоты (см. рис. 10), так и выше. Возможна также ситуация полной неопределенности (например рис. 10, 300 км), когда можно выбрать два центра масс, каждый из которых имеет свои температуры. Полученная в итоге температура для окна 300–405 км соответствует взвешенному среднему значению температур с высот ~210 и ~320 км.

В такой интерпретации нет никакой определенности относительно истинных температур именно для высоты 300 км. Вероятно, из-за эффекта Фарадея вообще невозможно получить какую-либо информацию о температурах для высот, соответствующих замираниям мощности сигнала.

ЗАКЛЮЧЕНИЕ

Разработанная методика решения обратной задачи на основе предложенной модели рассеяния сигнала дает быстрый и информативный подход к развитию методик определения не только температур, но и других важных параметров ионосферной плазмы, таких как скорость дрейфа плазмы, величины электрического поля, ионного состава и т. д. В дни спокойных геомагнитных условий и высокой концентрации электронов метод дает удовлетворительный суточный ход ионных и электронных температур. В других условиях используемое приближение обратной задачи не позволяет получить достоверные значения температур. Более строгий подход к решению радиолокационного уравнения заключается в его разложении в систему линейных уравнений и применении регуляризации (например, методом Тихонова). Алгоритм, реализующий такой подход, находится в разработке.

Для решения обратной задачи можно отказаться от каких-либо приближений, используемых при решении радиолокационного уравнения, если привлечь к анализу априорные ограничения и данные измерений других инструментов. Можно отказаться также от приближений прямой задачи и получить радиолокационное уравнение в наиболее развернутом виде. Это может быть оправдано с точки зрения допустимых объемов вычислений только при наличии решения в первом приближении и однозначном понимании физических явлений, которые могут вносить в эксперимент систематические погрешности. Предложенная модель сигнала обратного рассеяния дает такое решение. Кроме того, построив гипотезу об источниках этих погрешностей, мы можем быстро и эффективно оценить ее правдоподобность с помощью моделирования.

Работа выполнена в рамках базового финансирования программы ФНИ II.12. Результаты получены с использованием уникальной научной установки «Иркутский радар некогерентного рассеяния» [].

ПРИЛОЖЕНИЕ

Обозначив выражение S _nh e ^{( m} nh ^{+ 2} k ⁿh^{h + ф} "h ) как x ( t , n , h ), а выражение

I Ct 1 I

Q I hi — л J Q I h 2

ct  c τ

--+ -

T

| o ( t ) o ( t — т ) — как w (t, t , h 1 , h 2 ), получим:

ct              ^N

R ( ^т ) = Z Z ^F ( ^h ) ^x ( t , " , ^h ) Q I ^{h —} V I o ( t ) ^F ( ^h ) Z ^{x (} t ^{— т}, " , ^h ) ^e nh ^Q I ^h t = t    h                          V ² )               n =0                             V

—

c ( t — t) J / X --------- o ( t — т ) .

2 J

Используя свойство суммы

Z Ax Z By = ZZ AxBy, xx

xy

проведем ряд преобразований: T (

N

N

R ( т ) = Z ) ZZ [ F ( h i ) F ( h 2 ) w (t, t , h i , h 2 ) Z x ( t , " , h ) Z x * ( t - t, " , h ) e™ nh ^T

t =T I h , h .

n =0

T l„„                    N N                        ll

= Z)ZZF ( hi) F ( h 2 ) w(т, t, hi, h 2 ) ZZ[ x ( t, ni, hi) x ( t — т, " 2 , h 2 ) e "2 Jf = t=т I hi h2                                                    n ,=0"2 =0

(Далее нужно применить свойство суммы ZZ A x B y — ^Z A x B x + ^Z^Z A x B y последовательно для n и h )

xy

x

x y * x

T I                                              N N Г                                                       "ll

= Z) Z [ F 2( h )w(t, t, h, h) ZZ[ x (t, п,, hi) x * (t — t, n 2, h 2) e ™ n2 h2 т JU t =т I h, h2 = hi                                      ni =0n2 =0                                                                  l

T l                            NN

+ZlZ Z [ F ( hi ) F ( h 2 ) w ( T, t, hi, h 2 )JZZ[x ( t, ni, hi ) x * (t — т, n 2 , h 2 ) e ™ "2 h2 T J t = т I hi h2 * hl                                                        "i =0 "2 =0

T

= z[,z.

t =т I h , h 2 = h i

N                 ll T l

F ( h ) w (t, t , h , h ) Z x ( t , " , h ) e nh f + Z ) Z [ F ( h ) w (t, t , h , h ) x

• n , п , = " 2                                      t =т | h , h j = h i

N N V                                                  -i-ll T l xZ Z [x(t, "i, hi)x*(t — t, n2, h2)e™"2h2TJJf + Z)Z Z [F(hi)F(h2)w(t,t, h„ h2)x

" i =0 " 2 * " i                                                                     l t =T I h i h 2 * h i

N N I-                                         • -im T l xZZ[x(t, ", hi)x*(t— T, ", h2)e™"h2TJJ} + Z)Z Z [F(hi)F(h2)w(T, t, hi, h2)x п, =0 n 2 =0                                                                      t=t | h   h2 * hi

]])■

NN                 iωτ xZ Z [x(t, "i, hi)x (t — t, n2, h2)e п, =0 n 2 * п,