Модель слоистого течения вязкопластичной бингамовской жидкости в канале экструдера

Создание инновационных технологий в пищевой промышленности базируется на углубленном изучении процессов. Особенно важен теоретический анализ механизмов реализации зеленых технологий. Развитие теоретических и практических методов дает возможность создания прорывных технологий. При этом одним из важнейших направлений их создания является изучение гидродинамики [1–4], зачастую осложненной нелинейными компонентами [5]. В этом случае изучение и моделирование процессов вязкопластичной гидродинамики

особенно важно для дальнейшего развития пищевых отраслей [6]. Понятие о пластичных жидкостях впервые ввел Бингам, поэтому их называют бингамовскими вязкопластичными жидкостями, или бингамовскими телами [7]. Они отличаются от ньютоновских жидкостей тем, что для инициирования течения требуется приложить некоторое конечное напряжение [8].

Результаты и обсуждение

Консистенция идеальной бингамовской вязкопластичной жидкости, описывается уравнением:

т - т

^-Ц р

•

dv ( r ) dr

т

Ц е = Ц р ⁺ " ° .

Y e

где т - напряжение сдвига; т_о - напряжение, необходимое для начала течения жидкости; ц _р - пластическая вязкость, которая определяется как касательное напряжение, превышающее предельное сдвиговое значение и сообщающее жидкости единичную скорость сдвига; dv ( r ) -разность скоростей соседних слоев; dr – расстояние между ними; - dv ( r ) [dr - скорость сдвига, для градиента скорости dv ( r )/ dr , определяемого наклоном профиля распределения скоростей.

Следовательно, ламинарное течение вязкопластичной бингамовской жидкости определяется уравнением:

т

Ц р = т - (2)

Y

, где у - скорость сдвига, определяемая через градиент скорости у = - dv (r),dr, как наклон профиля распределения скоростей. График консистенции ньютоновской жидкости представляет прямую линию, проходящую через начало координат, а наклон этой линии определяет пластическую вязкость (2). Поскольку вязкость ньютоновской жидкости μ не зависит от скорости сдвига, она является единственным параметром, определяющим свойства потока ньютоновской жидкости, в отличие от бингамовской (1) вязкопластичной жидкости:

^т ( ^Y ) = ^т 0 + Ц р • ^{Y (3)}

Общее сопротивление сдвигу бингамовской вязкопластичной жидкости (3) может быть выражено через эффективную вязкость ц_е при определенной скорости сдвига ye . Эффективную вязкость при известной скорости сдвига γ е можно вычислить с помощью следующего выражения:

Сопротивление трения относительному перемещению слоев, или эффективная вязкость (4) определяется, как вязкость аналогичной ньютоновской жидкости, соответствующую конкретным значениям напряжения и скорости сдвига бингамовской жидкости. Таким образом, эффективную вязкость можно рассматривать состоящей из двух компонентов: пластической вязкости, соответствующей вязкости ньютоновской жидкости, и структурной вязкости, которая характеризует сопротивление сдвигу, вызываемое тенденцией содержащихся в бингамовской жидкости твердых частиц образовывать структуру [9]. Как видно из уравнения (4) т_о /у_е составляет часть общего сопротивления сдвигу, уменьшающуюся с увеличением скорости сдвига; следовательно, с ростом скорости сдвига эффективная вязкость снижается. Следует особо отметить, что эффективная вязкость имеет физический смысл, если указывается скорость сдвига, которой она соответствует. Тем не менее, эффективную вязкость вводят во многие уравнения гидродинамики [10], если известна эта скорость сдвига. Пластичное течение при давлениях ниже т_о представлено явлением ползучести. В этом виде течения эффекты сдвига не проявляются. Суспензия течет как жесткое ядро, смазанное тонкой пленкой у стенки канала, а в ядре частицы удерживаются вместе силами притяжения, действующими между ними. Зависимость давления от расхода при течении бингамовской вязкопластичной жидкости определяется фактическим предельным динамическим напряжением сдвига без учета ползучести р о и условным предельным динамическим напряжением сдвига (4/З)×р о , определяющим движение жесткого ядра относительно асимптоты течения бингамовской жидкости [11]. В случае течения в прямоугольном канале шнека [12], с движущимися стенками и неподвижной крышкой [13], скорость потока ньютоновской жидкости определяется уравнением:

W Z ( x , у , a , b ) = V -

”

-v<

■^

к = 0

4 • V          4 • b ²       А Р   /     2 • к + 1 )       4 • b ²       А Р

------------------3---- Ch I К- X --1 +--3----+ ^{к -} ( ² • k + 1 ) п ³ • ( 2 • к + 1 )    Ц V b У к ³ • ( 2 • к + 1 )    Ц

л , (       2 • к + 1

4 • sh \ к- x--

V ь

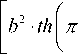
2 • к +1 / ----------------------------- • b )

--V • cth I к - a • ц V

2 • к + 1 b

. (       2 • к + 1

• sin к • у--

V b

Скорость потока (5) формирует градиент, который представляет собой вектор V W z :

,   8 W z ( x , y , a , b ) _

Z =-----"----------ex + dx d Wz (x, y, a, b) _

+------5-------ey dy

и, следовательно, использовать соотношение (8) для определения расходно-напорных характеристик в зоне ламинарного течения экструдируемой бингамовской жидкости. В данном случае важным показателем является скорость сдвига связанная с модулем градиента соотношением

определяющий наклон профиля распределения скоростей. Скорость сдвига определяется как модуль градиента скорости слоистого течения (6) в направлении движения канала с габаритами a×b по оси Z в его прямоугольном сечении по осям X и Y:

I A

d WZ (x, y, a, b) dx d WZ (x, y, a, b) dy

dv ( r )

dr

d W Z ( x, y, a, b )

у       d x

Соотношение (7) эффективную вязкость

+

d W Z ( x, y, a, b )

2. (7)

dy позволяет определить ламинарного течения

по прямоугольному каналу:

Ц е = Ц р ⁺

позволяющим локализовать зону пластичного течения экструдируемого материала в канале шнека. В случае т ₀ = ц _р • X наблюдается граница течения в виде жесткого ядра. В результате расчетов по зависимостям (5) и (7) были получены диаграммы линий уровня скоростей слоев w и скоростей сдвига γ для усредненных показателей (габариты канала 40×150 мм; скорости стенок канала 1,5 м/сек; градиента давления 700 кПа/м; и эффективной вязкости материала 100 Па×сек) промышленных шнековых прессов (рисунок 1) .

+

d W Z ( x, y, a, b )

^T o

+

d W Z ( x, y, a, b )

dx dy

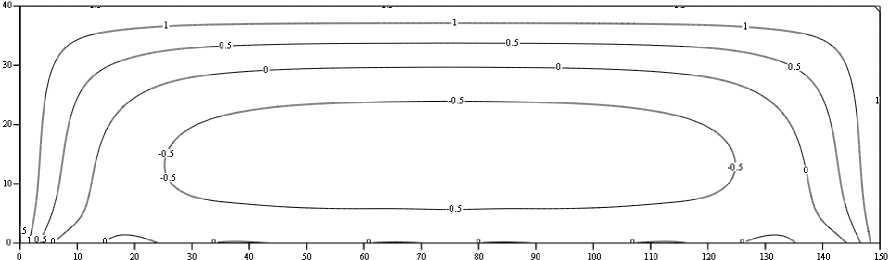
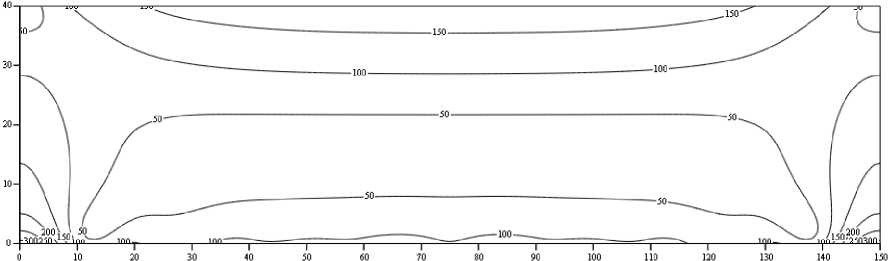
Рисунок 1. Диаграммы линий уровня скоростей слоев w и скоростей сдвига γ для усредненных показателей промышленных шнековых прессов

Figure1. Diagrams of the layer velocity level lines w and shear rates γ for the average values of industrial screw presses

Как видно из представленных данных (рисунок 1) в канале шнека присутствуют зоны вынужденного потока создаваемого динамическим напряжением сдвига и обратного потока создаваемого избыточным давлением сопротивления головки. Скорость сдвига в канале шнека отличается значительной неоднородностью и определяет сложный характер деформации сдвига материала в процессе экструдирования.

При давлениях превышающих давление р о , при котором начинается пластичное течение у крышки канала, начинается ламинарное течение. При давлениях, превышающих р о , ламинарное течение постепенно охватывает остальные слои, и поток представляет собой жесткое ядро, окруженное зоной ламинарного течения [14]. В вязкой жидкости касательные напряжения в центральной плоскости течения равны нулю. Поэтому около этой поверхности будет формироваться пластинчатое ядро, где т <  т 0 . Напряжения внутри этой области будут чисто упругими, и оно будет двигаться как жесткое целое. При x = x _o ; y = y _o имеем d/drW Z ( x,y,a,b ) = 0. Следовательно, для x ≤ x о и y ≤ y о , хотя и есть движение, течение отсутствует. Область локализации пластичного течения определяется равенством:

для усредненных показателей промышленных шнековых прессов (рисунок 2) . Для выделения пластичного ядра используем уравнение (9) определив положение пластичного течения относительно координаты x, для у с = b /2:

dW_Z ( x, y c , a, b )

dx

= 0

x ₀

Из соотношения (10) определяем положение средней части зоны пластичного поршневого течения (xo = 11,51 мм) и определив скорость сдвига на границе этой зоны dW x ,y ,a,b

—z ( o, c, , ) = 33.93 Гц dx определяем её положение относительно средней линии из системы уравнений:

dW z ( x o , У с , a , b ) = dW z ( x ^ , У с , a , b )

dx              dx dWz (xo, Ус , a, b) = dWz (x„, Ус , a, b)

dx              dx

Определив положение границ зоны пла-

d W z ( x , y , a , b )

d x

6 W_z ( x , y , a , b )

d y

= 0

стичного течения на оси симметрии из системы уравнений (11) выделяем зону пластичного течение по скорости сдвига соответствующей найденным значениям координат. При этом скорость поршневого течения в этой зоне определяется соотношением

^x = x o ; y = y о

Учитывая симметричность задачи относительно середины канала по оси Y рассмотрим одномерное уравнение при у с = b /2течения в рамках бингамовской реологической модели

W z ( x o , У с , a , ^b ) , которое получаем подстановкой найденной координаты x _o из уравнения (10).

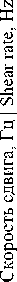
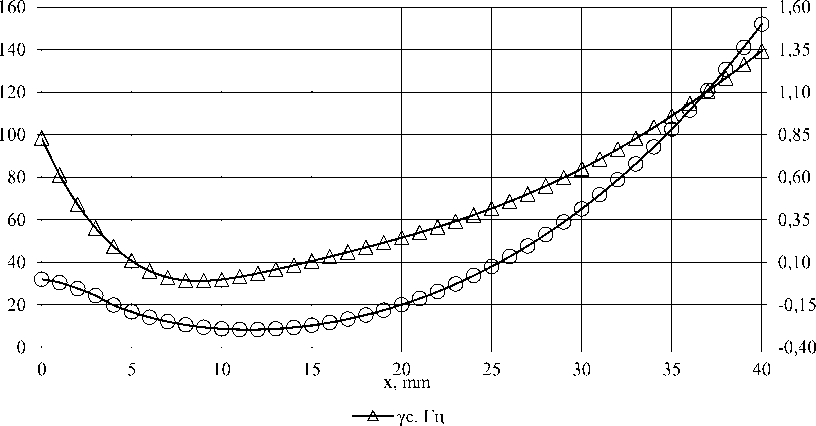
Рисунок 2 Распределение скоростей слоев w с и скоростей сдвига γ с по оси симметрии канала

Figure 2.Distribution of velocities of the w s layers and shear rates of the γ s along the channel symmetry axis

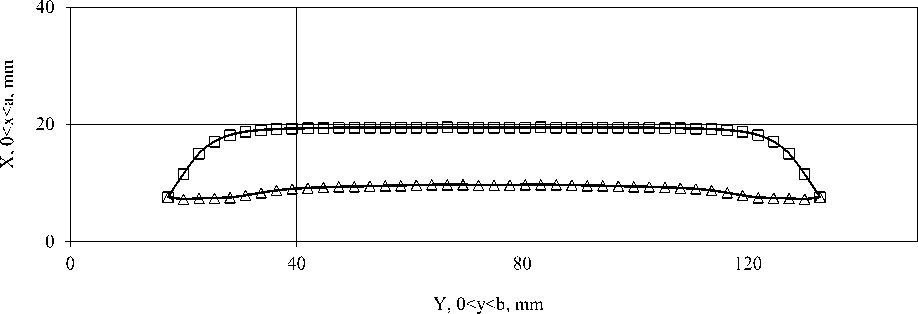
Таким образом, течение в пластичном ядре канала экструдера представляет собой течение с жестким ядром (рисунок 3). При этом напряжение в этой области не превышает предел текучести. Абсолютного предельного динамического напряжения сдвига не существует, поэтому бингамовское предельное динамическое напряжение сдвига, это напряжение сдвига, необходимое для инициации ламинарного течения суспензии. Если давление постепенно увеличивать от нуля, суспензия вначале движется как жесткое ядро, а профиль скоростей представляет собой прямую линию, перпендикулярную к оси Z. Вне зависимости от амплитуды давления, жесткое ядро полностью исчезнуть не может, ибо при очень малых габаритах ядра значение давления должно быть весьма большим, а при исчезновении пластичного течения должно стать бесконечным. Таким образом, зависимость напряжения сдвига от скорости сдвига для течения бингамовской вязкопластичной жидкости всегда нелинейная при любых значениях скорости сдвига. Следовательно, важным элементом расчета расходно-напорных характеристик процесса экструдирования является локализация пластичного течения в канале шнека.

Xл Xп

Рисунок 3. Геометрия зоны пластичного ядра в канале экструдера

Figure 3. The geometry of the plastic zone of the core in the channel of the extruder

Заключение

В результате проведенного анализа модели слоистого течения вязкопластичной бингамовской жидкости в канале экструдера