Модель стратифицированной смазки упругодеформированного радиального подшипника

Введение. Имеется практический и теоретический интерес к исследованию упругодеформируемых подшипников [1-3]. Выполненные исследования в этом направлении [4, 5] показывают, что упруго-деформируемые подшипники обеспечивают большую устойчивость при работе на высоких скоростях и малых нагрузках, чем жесткие подшипники. Существенный недостаток существующих расчетных моделей упругодеформированных подшипников состоит в том, что в них не учитываются особенности взаимодействия смазочной жидкости с твердой круговой опорной поверхностью подшипника, в результате которого происходит расслоение смазки на слои с разной вязкостью. В известных работах [6, 7], посвященных расчету подшипников, работающих на двухслойных смазочных материалах, опорная поверхность предполагается жесткой и, кроме того, поверхность подшипника считается сплошной. В работе [8] приведена расчетная модель упорного подшипника скольжения, работающего на трехслойной смазочной композиции с учетом деформации его опорной поверхности, где рассматриваемый подшипник не обладает демпфирующими свойствами. Целью данной работы является обобщение предложенного в работе [8] метода для случая радиального подшипника, работающего на двухслойной смазочной композиции и обладающего повышенной несущей способностью и демпфирующими свойствами.

Постановка задачи. Рассматривается установившееся стратифицированное течение двухслойной смазки в зазоре упругодеформируемого радиального подшипника скольжения, обладающего демпфирующими свойствами. Предполагается, что подшипник с адаптированным профилем опорной поверхности содержит упругий слой и неподвижен, а шип с пористым слоем на его рабочей поверхности вращается с угловой скоростью П. В полярной системе координат уравнения контуров С ₀,С₀, C_v С_г,С_у С₄ (рис. 1) можно записать в виде:

С₀:r' = r₀; CV-r' = r₃+H; С 1 : г' = r_a + Н + 5а + aecosO - a/sinco0 + ('f(6);

С₂:r' = г₂ + ecos9-/sinco9; С ₃: г' = г₂ + е cos 9-/1 sin ю9 + XT^Y,

С ₄: r' = r₃ + е cos9 -ZsinraO,

Работа выполнена в рамках инициативной НИР, где а е [0,1]; Н — толщина пористого слоя, мм; г0 — радиус шипа, мм; 8 = г2 - г; А и со — соответ-

-1

ния контура опорной поверхности подшипника от кругового); X'f (9) — ограниченная функция,

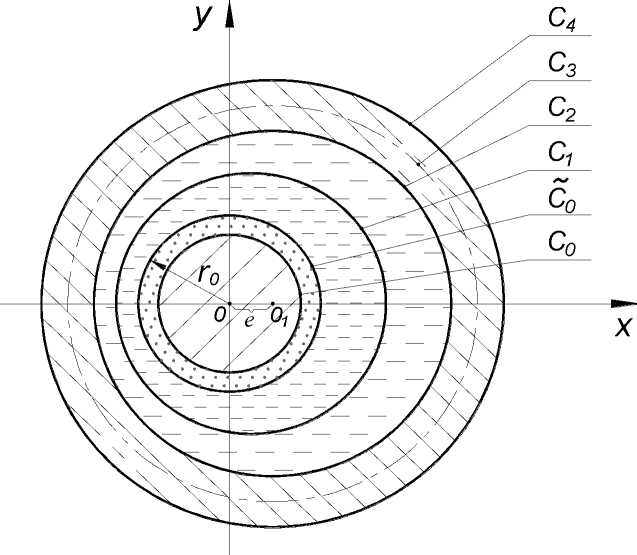
Рис. 1. Схематическое изображение шипа с пористым слоем в упругодеформированном радиальном подшипнике: С о - внутренний контур пористого слоя шипа, прилегающий к непроницаемой поверхности; С_а - внешний контур пористого слоя шипа, прилегающий к смазочному слою; С 1 - граница раздела 2^-х смазочных слоев;

С ₂- внутренний контур подшипника, прилегающий к смазочному слою;

С з- деформируемый контур упругого слоя подшипника; С „- внешний контур подшипник

Решение задачи. В качестве основных уравнений примем безразмерную систему уравнений движения вязкой несжимаемой жидкости для случая «тонкого слоя», уравнение неразрывности, уравнение Дарси и уравнения Ламе:

9 ²ц,    dp,

^{2              ,}

“ - ’     0, аг ге

8 2и .

"9^0 ^{= 0,} 8г

²P ,1 дР , 1 S²P _ _n ^{( 1,2)}, 8C \ 8Q e se² 0, ^ = 0.

dr *²

Величины г',u'_i,d_i,p’_i в смазочном слое связаны с безразмерными г,^,^, и р_; соотношениями: (г₀+/У) ²

г'= г_;- Н-Ar, u'=Q/ou„ и’=Ойи_н # = р,р_и Pi ~    ^v02 —-- z^M,

О где

и', , и' — компоненты вектора скорости, мм/с; р, — гидродинамическое давление в смазочных слоях, Па; ц, — динамический коэффициент вязкости, Па-с.

В пористом слое переход к безразмерным переменным осуществляется по формулам где

где

г' = Н-^ , Р' = р*Р,

Р’ — гидродинамическое давление в пористом слое.

В упругом слое переход к безразмерным переменным осуществляется по формулам r' = r+8,r *, 8,=r-r, u'=u*u_r, и'=и*и_л,

2  1   132

u'_r ,u' — компоненты вектора перемещений.

Граничные условия на поверхности шипа и подшипника записываются в виде:

д| г q="N —

¹¹ ос.

, UJ

S=7+1

ЭР

-0 = 1, Д(0) = Л(27Г) = Д; —

= 0; д = Д| ,;

' Г 1      1^=у+1 '

^=7

u21 г=Л(е)

= 0, U2|^(6)=0, Д(0) = Д(2тг) = Д.

На границе раздела слоев граничные условия записываются в виде:

и 1 | r=ah

- ^U2 I r=ah , ^U1 |

•=ah = и 2 |

■=аЛ ,

Эи i I dr 1

Эи 2

6г

■=аА , и,1

•=аь = ^ (9),

kCr.-vHA ²

h (9) = 1 + _ncos9-_n1sinco9 + V(9), _n = e/5,m=/l/5,/V = -⁽^-₃ -,Y = T0, /- т

■

/70         П О

Граничные условия (5) означают прилипание смазки к поверхности шипа и подшипника, периодичность гидродинамического давления, а также то, что при переходе через пористую поверхность давление меняется непрерывно, а нормальная составляющая скорости определяется законом Дарси. Кроме того, на непроницаемой поверхности шипа нормальная составляющая скорости равна нулю.

Условия (6) означают равенство скоростей, касательных и нормальных напряжений на границе раздела слоев, а также условие существования слоистого течения смазки, т.е. требуется, чтобы скорость точек границы раздела слоев в каждой точке была направлена по касательной к контуру раздела слоев.

Граничные условия для уравнений Ламе записываются в виде:

8u_r I             ~ I

'M-w ■

- ‘^(е) "^Ur* |

(е) - 0,

где р- тахд, 9 е [0,2л]; р_т — безразмерное гидродинамическое давление, найденное в работе [9], в случае подшипника с жесткой опорной поверхностью, работающего на двухслойной смазке; (1 + а>*8²

Мт. ---к---;--- тт~ ; а - постоянная Мусхелишвили; С — модуль сдвига; М — упруго-

(1-а )ц₂ю(г₀ *НуЭ₁

гидродинамический параметр;

а А                е А

h. (9) = —cos9--sinco9, h. (9) = 1 + — cos9 — sinm9.

51                1                   ²                  1               1

Полагая толщину пористого слоя достаточно малой, уравнение Дарси усредним по толщине этого слоя [10]

Чз2Р 1 8Р UP

У

2 ;       ^2 so2

си; = 0.

Точное автомодельное решение системы уравнений (2), удовлетворяющее граничным условиям (5) и (6), с учетом (9), ищется в виде:

u^-^ + U,(г,9), и, =^ + 1<(r,9), %=ТЛ), or и,о,^^^) v^-.^. 4, ^44. ^44. Р = А (9) ^ - у)2 (С - (у + 1))2 + С * (С - у)2 Л'(9)К - (г +1)] +Р,, "^V^2^.

Подставляя (10) в (2) и в граничные условия (5) и (6), с учетом (9), получим:

V1 =4. V, =4. ц +W =^U) V₂ =4. ^^l ^2 +^2= 0,

V1X0) = 0, Z/l(0) = -Af*, б1(0) = 1, v2(1) = 0, ед = 0, б2 (1) = 0, уу' (а) = \j>2 (а), б, (а) = б, (а), ц (а) = ^2 (а),

2--/               2         /-1—^2

” 1 к<^2 — ^1!-А^Л Ч'1(^)---- 'I'2 V^X), А -— Р21

*        Ц1 "                  МтР1

Jg 1U) + fG2UM = -/Vt*=P*.

0а

Учитывая, что расслоение смазки на слои происходит вблизи неподвижной твердой поверхности, т.е. при значениях а ,, близких к единице, условие раздельного течения смазки (ц(а) / б, (а)) = а//(9) в принятом нами приближении удовлетворяются. Из граничного условия

О ₂ (с/) + ай₂ ((х) + J б₂ (СТгА = 0

следует, что

_ , . U-, (а)

»2 ⁽«1 ^ГСТ +

112(а)

г ^С-Ж

2 (^)

= 0.

Используя теорему о среднем значении, получим:

_ , .      (а)

»2 ⁽«J v-tct ।) ₂ (а)

221212(1 __а) =0, а * е(а, 1). и 2 (a)         J

*

Так как и₂(«*)< 62(a), (1-а)«1, следовательно, с точностью до членов О

б , (<х*)

_² , , (1 - а) ,

будем иметь

J6 1 (6)^ + /^" .0, |б₂(²)^,0. 0                             a

Решение задачи (11)—(12) находится непосредственным интегрированием. В результате

-: 2

2 2

Т 1 — ^С2 2 ⁺-2^ ⁺ Tз^,

V2 ^{= С}2 ~ ⁺ ^^ ⁺ ^^, 2

и 1 =-<:₁ч₇-c^- + C1₀^, 3

¹ 2

- ?2

ч = Р ~

^{2      1} 2

+ С S^ + C9,

°^{2 =} ”^Е3 ^

^ 2

^С 8 2 ⁺^"11^,

Р 1 — <-1-72 (6) + 2-7з(6) + C₁2^,

Р 2 — <-1-72 (6) + С_гЛ( (6) + С1₃^,

е

Л P) = f

___________ de ___________

(1 + я cos 0 - т^ sin®0) + (fW

Для определения постоянных с, (/=2,3,...13), с ₁, q, q,q решим следующую алгебраиче

-16-

С7 = 1.   Сщ = Р з ,   Сз = 0.   С12 =

= 11    _  = 11

-q - .-^,,0.  с--

3    2              22

Q з=Рд,

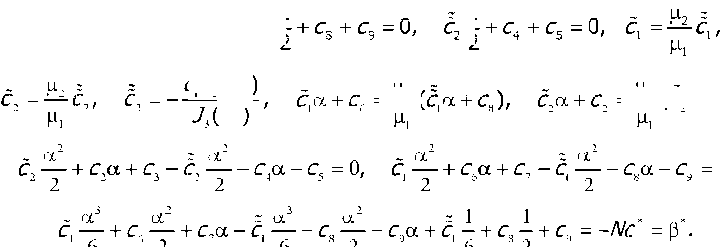
С J2V2) (2 it)

0 ,

2 ₍

= —(q,x + q),

Решение системы (18) сводится к решению следующего матричного уравнения:

М • х = Ь ,

где x = fq;q;q;q; С9

м =

_ _^7l)

J 3 (2л)

(1- ^)а2 2^(2^

J з (2л) а² (к -1)

Решая систему (18), получим

= 6 + 213* 1

2	2	0	0
0	0	2	2
0	0	3     2    3 2    3	66
2а (к - 1)	2	0	0
0	0	2а (к - 1)	2

.

6   2 62

А

2оф2 + а ^р*

,

. = Л^2л) 4 Л (2л)

-—   ---г— (3 - 6а2 - р*а2 + 3а4 + р*а3 - оф* + а3^2р* +

+3к2а4 + а^р* - 2а3кр* +|<^а2 - 6ка4), q = - 2^ — • ----------г—а(-3а2 - 3а - 2ар* + 3а3 + р*а2 + р* + р*^2а2 + 3 +

• ⁵    J₃ (2л) (ак -а + 1

+6каР - 3к + 3а?к² - р*^ - 2р *к а² + 3а^р* - 3а² к² - р*^²а - 6ка³ + 3а к),

4 - р*а2 - 4а3 + р*А"а2 + 4Д-а3 + р*

А

-4а³ + 4^а³ - 3ка? + р*^а² + 3а² - р*а² + ар* - а^р* +1

А с 2  кс4. с6  кс^.

А = -4а³ + 1 + а⁴ - 6ка? + 4£а³ + Хт²а⁴ + 4£а - 2ка-⁴ - 4а + 6а²,

С 1 =<, 2, =-£1

J 2 (2л) j 3 (2л)■

Таким образом, для определения поля скоростей и давлений необходимо найти функцию Xf (9), характеризующую деформацию опорной поверхности подшипника.

Для определения этой функции воспользуемся приближенной формулой

1^ (Ф^ф-ш-м.                   (21)

Таким образом, из найденного выражения для функции Xf (9) следует, что при М -> со, u_r -> 0 (это соответствует случаю жесткой опорной поверхности подшипника).

(

h (9) = (1 + Xf^9^ (1 + f|cos9 - л, sin соб) =

М

(1 + fj cos о - и, sin соО), n = —^, 11

М

1 ₊ ^' М

С учетом (22) на основании граничного условия р ₂(0) = р₂(2л)

для

выражение:

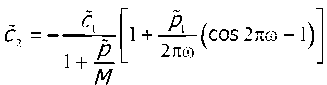
p1

с ф sin 9

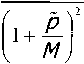
Г n (cos mil - Il 11

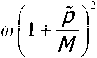
СTi. 9(cos 2лсо-1)  Д z    Гт   I" “Г

I      b .2 P l м)

Основные рабочие характеристики подшипника запишутся следующим образом

^Ry _ ²f ^dP_x               5        ■ 91 rcos(™ -1)2tc-1 , cos(co + 1)2л-1

* — I ----COsУс/У —----— ЛТ| । --- ----------------Я-- p r ,   0 uQ            1 + P_ L     2 m       co -1              co +1

M

R_{x =} _²f dp 1 sin_Q^_{Q =} _ f _{1 +} Э,^ От Г sin(m - 1)2л _ sin(co + 1)2ti p * r₀     { dQ             ( M) 2co L CO -1          co +1

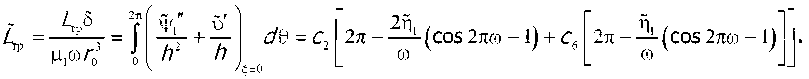
Анализ полученного аналитического выражения для безразмерной несущей способности R_y

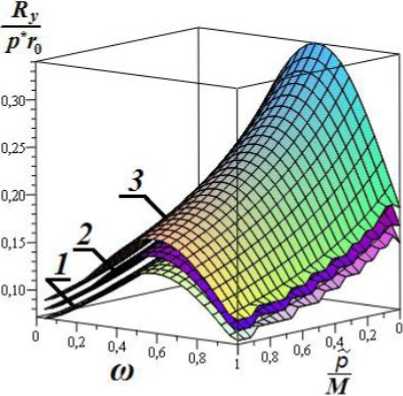
Рис. 2. Зависимость безразмерной несущей способности от параметров

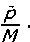
• 1 )    М = 100 ,     р* = -0, 1 ;

• 2 )    М = 1000 , р * = -0, 1 ;

• 3)    М -» со,     р* = 0.

Рис. 3. Зависимость безразмерной несущей способности от параметров

.

• 1 )    £ -0 , 01 ,     р*= -0 , 1 ;

2 )^ =0 , 001 , р*= -0 , 1 ; 3)^ -0,        Р* =0 .

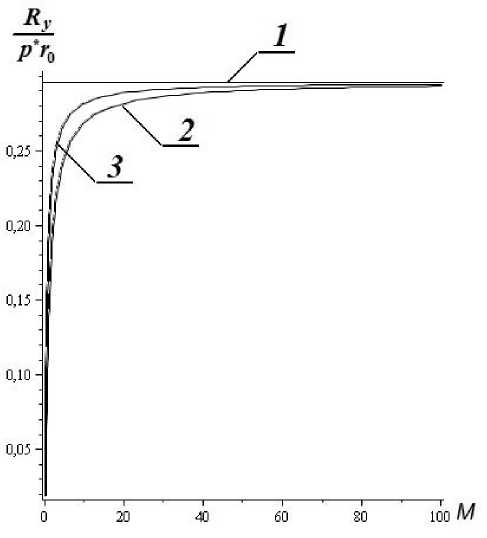
Рис. 4 Зависимость безразмерной несущей способности от параметра М

1 ) £ = 0 , Р* = 0 ;   2 )     = 0 , 02 , р* = -0, 1 ;   3 ) £ = 0 , 01 , р* = -0, 1 .

Выводы. Результаты численного анализа, приведенные на рис. 2-4 показывают:

• 1.    Несущая способность подшипника существенно зависит от значения упругогидродинамического параметра М . На рис. 4 проиллюстрировано, как с увеличением значения параметра М повышается несущая способность подшипника.

• 2.    При Л/ —> ос несущая способность подшипника стремится к соответствующему значению для подшипника с жесткой опорной поверхностью.

• 3.    С увеличением значения параметра р^* , обусловленного наличием пористого слоя на поверхности шипа, несущая способность подшипника незначительно снижается.