Модель сверхпластичности, основанная на представлениях о кооперативном зернограничном проскальзывании

А/

Заметим, что выражение для скорости дислокационной ползучести содержит дополнительный (в сравнении с [8]) множитель P_d(t,), связанный с распределением зерен по размерам. Переход в режим дислокационной ползучести происходит при условии: размер ячейки дислокационной сетки меньше размера зерна. Размер ячейки определяется дейст вующим напряжением и параметром материала К из выражения (2). Если материал состоит из зерен разных размеров, то дислокационная ползучесть начинается в первую очередь в наиболее крупных зернах. При увеличении напряжения происходит последовательное подключение мелких зерен. Те. фактор Р_п(т, < L >) задает парциальный объем материала при данных т и , в котором протекает процесс дислокационной ползучести. Как следует из соотношения (7) при увеличении напряжения P_D —> 1 и тогда выражение для скорости дислокационной ползучести переходит в известное выражение [8].

Характеристики модели

Принципиальное отличие предложенной модели от существующих связано с дополнительным фактором <М>/Мо в выражении для скорости деформации (1). Как следует из предыдущего, этот фактор определяет интервал СПД в пространстве параметров материала и условий нагружения. Анализ этого интервала приводит к следующим результатам.

Поскольку в выражении (5) п»1, то необходимое условие отличия <М> от нуля сводится к неравенству

МАХ {рв(т, < L >)) > pt,                           (9)

t, которое с использованием приближенного представления Ф(х) х ^7-ехр( 4х2 / лL х>0, принимает вид

J К bL 1

_{2 <}  ^1П 116

(Ю)

2л|1п(1- р2)|

Известно, что после СПД в материале формируется однородная равноосная структура. Как следует из неравенства (10), условие однородности структуры является необходимым условием формирования полос КЗГП Верхний предел дисперсии определяется перколяционным порогом рс, параметром К, контролирующим переход в режим дислокационной ползучести, и соотношением векторов Бюргерса решёточных и зернограничных дислокаций, т.е., по сути, наличием в материале достаточного количества произвольных границ зерен. Следует иметь в виду, что начальное распределение зерен по размерам может иметь дисперсию, превышающую верхний предел, диктуемый условием (10). Однако при этом стадия выхода в режим стабильного течения должна протекать в условиях активной динамической рекристаллизации, обеспечивающей структурную проработку материала. Если же стадия стабильного течения достигнута (а только она и рассматривается в данной модели), то конечное распределение зерен по размерам должно иметь малую дисперсию, т.к. это необходимое условие формирования полос.

Как следует из соотношения (5) и проиллюстрировано рис.2, при заданной температуре испытаний существует максимально допустимое значение среднего размера зерен. В материалах с размером зерен, превышающим это значение, не происходит формирование полос КЗГП, а, следовательно, и невозможна реализация режима СПД. Из выражений (4) и (5) нетрудно получить явное условие на средний размер зерен:

м bL < bL

2 ГК X(T)U

4 bL „

--exp —-7D. b в l 2

D2

^|1П(1 - Рс)| ■

Известно, что повышение температуры позволяет реализовать режим СПД в материале с более крупным зерном. Выражение (И), воспроизводя эту тенденцию, позволяет сформулировать и более сильное утверждение: температурная зависимость максимально допустимого значения среднего размера зерен определяегся температурной зависимостью коэффициента поверхностного натяжения границ зерен. Величина M при прочих равных условиях контролируется значениями дисперсии и перколяционного порога, т.е. физическими параметрами, не учитываемыми известными моделями СПД. Значимость зависимости M от D и рс иллюстрируется рис.3, полученном при следующих значениях параметров; /о=О,О2; K=bi/bB=10, T/Tm=0,75.

При выполнении условий (10) и(11) нетрудно оценить интервал напряжений, в котором происходит формирование полос КЗГП:

T^CTCTh,(12)

где тш      ЬВМУ  Г31

” = 2х(Т)^ - exp — R + A ,(13)

Th        Ьв (4У   Г

-^ = 2Х(Т)^ - exp R- —А(14)

Во        bL VKV    L   4

R2

= 1п2

^в

2b_L бкУ с" ²

7(f)

7    4

14D2 In -, 3

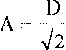
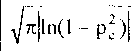
2 In 2

V^M1 " P=)L

Величина т± имеет смысл порогового напряжения, превышение которого приводит к формированию активных полос КЗГП. Правая граница интервала (12) ть определяет

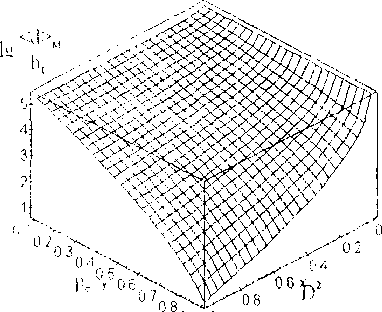
Рис.З. Зависимость максимально допустимого среднего размера зерен от значений перколяционного порога и дисперсии распределения зерен по размерам переход от режима СПД к режиму дислокационной ползучести. Нетрудно заметить, что выражения (13), (14) выдерживают контрольный предельный переход D—>0, вырождаясь при этом до соотношений, определяемых непосредственно границами интервала (2). В этом случае величина ть перестает зависеть от температуры, пропорциональна постоянной К и обратно пропорциональна среднему размеру зерна.

Пороговые напряжения при D -» 0 зависят от температуры, как (1 —Т/ Тт ) 2, и от размера зерен, как "3"*. В общем случае От 0 зависимость rf от температуры может усиливаться до ос(1 -Т/ Tm )2v, при этом зависимость от среднего размера зерен ослабляется, вплоть до полной независимости при достаточно высоких значениях D. Анализ температурной зависимости экспериментальных значений пороговых напряжений обычно выполняется в предположении, что cth осехр(Е/ кТ) В ряде случаев это оказывается оправданным и приводит к хорошо определенному значению энергии активации Е [9]. Однако нетрудно заметить, что экспериментальные результаты для высокоскоростной СП [10] лучше аппроксимируются линейной (ош оса-ЬТ), чем экспоненциальной зависимостью. Возникающая при этом проблема неоднозначности интерпретации может быть связана со следующим обстоятельством. Величина скорости деформации в интервале (12) определяется, в соответствии с соотношением (1), значением скорости сдвига V вдоль полосы. Причем механизм, контролирующий скорость сдвига V, может иметь собственное пороговое напряжение т0] , отличающееся от Tlh . Если <тл , то интервал СП определяется условием (12), если же выполняется обратное соотношение т7 > т^2, то интервал СП сужается

„                                   (2)   „               „ и роль пороговых напряжении переходит к величинетц, . Г.е. реальный вид температурной зависимости пороговых напряжений определяется температурной „                        (1)    (2)

зависимостью максимальной из величин тш , Tth ; при этом пороговые напряжения т^, ответственные за формирование полос КЗГП, зависят от температуры в соответствии с выражением (13) степенным образом, а напряжения т^, связанные с аккомодационными процессами, обеспечивающими сдвиг вдоль полосы КЗГП, -активационным. Тем самым в представления о СП вводятся понятия пороговых напряжений первого и второго рода: порог т^ определяет переход к формированию полос КЗГП, а порог т^ задаёт условия активизации механизма, контролирующего скорость сдвига вдоль полосы.

Даже не конкретизируя механизм, контролирующий скорость сдвига вдоль полосы КЗГП, мы можем получить на основе соотношений (12-14) ряд следствий, определяющих особенности СП в различных её проявлениях. Так для сверхмелкокристаллических материалов интервал оптимальных напряжений (12) перемещается в сторону более высоких значений. Величина этого сдвига легко оценивается. В пределе нанокристаллических размеров зерен пороговые напряжения т ^ перестают зависеть от температуры (что непосредственно следует из условия (2)) и может быть реализован режим низкотемпературной СП.

Обычный путь к высокоскоростной СП - это малый размер зерен и высокая температура, что, однако, приводит к проблеме структурной стабильности, решаемой через создание условий, подавляющих рост зерен. Другой путь - это высокие напряжения. Однако их нельзя повысить за пределы правой границы интервала (12), т.к. при этом деформация переходит в режим дислокационной ползучести. Отодвинуть правую границу интервала в сторону более высоких напряжений можно, увеличив значение параметра К, т.е. обеспечив меры по подавлению дислокационной ползучести (либо включения, либо высокие барьеры Пайерлса). Именно поэтому композиты и керамики - типичные объекты для высокоскоростной СП. Однако следует заметить, что принятые меры не должны подавлять возможность локальной подстройки ГЗ в окрестности тройных стыков, т.е. условия формирования полос должны сохраняться.

Заметим, что при построении модели основной акцент сделан на экспериментально установленной природе крупномасштабной картины течения, проявляющейся в формировании полос КЗГП, которые обеспечивают однородность деформации и отсутствие концентраторов напряжения, т.е. собственно режим СП. Поскольку мы считаем деформационный режим, основанный на активизации полос КЗГП, отличительным признаком, характерным для любого вида СП, то мы полагаем, что предложенная модель обладает достаточной общностью и должна работать в широком интервале условий от низкотемпературной до высокоскоростной сверхпластичности. В качестве иллюстрации на рис.4 приведено сравнение экспериментальных результатов по высокоскоростной СП в дисперсно-упрочненном композите [11] с результатами расчетов по предлагаемой модели. При расчете использованы следующие значения параметров: Т,_п=930К, Ьь=2,86*10¹⁰т, Ьв=Ьь/Ю, ц(Т=ЗООК)=2,54*Ю^1ОРа,         = -0,5, v=l/3, 5=2b_L, D_L0=l,7*10"⁴m²/c, Ql=1,8Q_b,

Po dT

5DBo=5*lO'14m3/c, Xo=O,O12, 2y=l,35, K=36, =0,68*10"6m, D2=0,5. Происхождение некоторых из этих параметров определяется температурными зависимостями модуля сдвига, коэффициентов диффузии и коэффициента поверхностного натяжения границы зерна:

TmdpT-300

ц(Т) = ц(Т - 300К)

1 +        ----L D - Dn exP(-Q/RT), Z(T) = Xo(1 -T / Tm)2'.

Bo dT Tm J

Остальные параметры определены выше. Энергия активации зернограничной диффузии Qb, в соответствии с результатами [11], выбиралась зависящей от температуры: Рв(733К)=130к1/то1, Ов(763К)=127кЗ/пю1, QB(793K)=122kJ/mol. И, наконец, перколяционный порог р_с, являющийся свободным параметром в рамках рассматриваемой модели, выбирался из условия совпадения с экспериментом. При этом получены следующие значения: р_с(733)=0,816, р_с(763)=0,635, р_с(793)=0,285, те. повышение температуры облегчав) кооперацию, понижая порог. Точность воспроизведения семейства зависимостей, полученных при трех разных температурах,

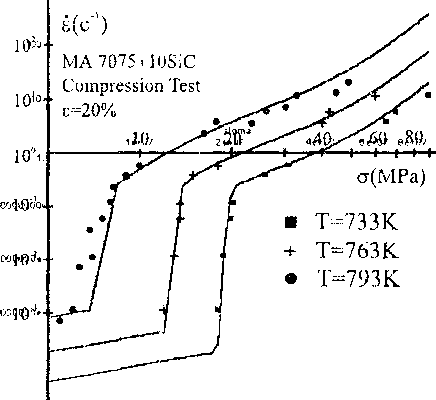
Рис.4. Зависимосгь скорости деформации от напряжения: точки -эксперимент [11], кривые - расчет по формуле (8)

оказалась вполне удовлетворительна. Возможность реализации высокоскоростной СП в данном материале определяется высоким значением параметра К, контролирующего переход в режим дислокационной ползучести. Высокое по сравнению с металлами [5] значение К определяется тем, что однородно распределенные дисперсно-упрочняющие частицы, во-первых, накладывают дополнительные ограничения на размер ячейки дислокационной сетки, формируя меньший эффективный размер зерна; и, во-вторых, ограничивают подвижность дислокаций, препятствуя термоактивированному выбросу парных перегибов (отметим, что в керамиках, также демонстрирующих возможность высокоскоростной СП, эту роль играют высокие барьеры Пайерлса). В совокупности эти факторы эффективно подавляют переход в режим дислокационной ползучести, сдвигая границу перехода в область более высоких, по сравнению с металлами, напряжений и не препятствуя формированию полос КЗГП.

Привлекательной особенностью модели является то, что условием реализации режима СП (как в пространстве параметров нагружения, так и в пространстве параметров материала) выступает единственный обобщающий признак: <М>*0. Как следует из выражения (5) и проиллюстрировано рис.2, это условие определяет нижнюю Тд и верхнюю тк границы интервала напряжений, максимально допустимый средний размер зерен и зависимость этих величин от температуры испытаний, дисперсии распределения зерен по размерам и другие параметры материала. При этом пороговые напряжения тш имеют принципиально другую природу по сравнению с известными, это не напряжения, при которых происходит передача деформации через изолированный тройной стык, а напряжения, при которых начинается формирование полос КЗГП. Как следует из проведенного рассмотрения, для этого недостаточно обеспечить совместность сдвига через некоторый ‘средний’ стык, - необходима модификация их определенного количества.

Предложенная модель не свободна от вопросов. Не исследовано влияние порообразования на условие формирования полос, механизм динамического переключения полос и др. Для получения надежных количественных результатов необходима более тщательная оценка качества приближения, приводящего к исходному условию миграциии (2). По некоторым признакам оно представляется излишне ‘жестким’. Однако сформированный подход уже сейчас позволяет единообразно объяснить многие экспериментально установленные факты: однородную структуру после СПД; существование верхнего предела для среднего размера зерен; природу интервала напряжений, в котором может быть реализован режим СПД. Развитые представления позволяют анализировать различные предельные варианты СПД. Широкий набор характеристик материала свободный от эмпирических параметров внушает надежды на выделение достаточного (полного) набора значимых материальных констант, необходимых для формулировки определяющих соотношений режима СП

Авторы благодарны профессору Р. А. Васину за полезные замечания.