Модель связи вертикальных деформаций с возникновением циркуляционных сил в системах «колесо - рельс»

Введение. Оценка динамики сложных современных систем невозможна без учета процессов, возникающих в результате действия сил трения. При этом для многих систем трение является не каким-то побочным явлением, от которого по возможности избавляются, а процессом, которым можно и нужно управлять. Управление невозможно без разработки адекватной математической модели, отражающей основные закономерности и характеристики процесса, которым предстоит управлять.

Процесс формирования и разрушения фрикционного контакта в узлах трения зависит от динамики движения самой системы, которая, как известно, определяется фазовыми траекториями. Оценка влияния фрикционного контакта на динамику систем управления носит эмпирический характер. Так, к примеру, в железнодорожном транспорте формирование силы тяги локомотива в узле «колесо – рельс» описывается нелинейной функцией, полученной усреднением статистических данных по динамике локомотива на заданном отрезке пути [1]. Такое представление о силе трения носит статический характер, не учитывающий динамику формирования и разрушения фрикционного контакта. Использование статической теории в моделях движения потребовала разделить тангенциальное усилие, возникающее при фрикционном контакте на силы трения: качения, сцепления, скольжения. Такая дифференциация оправдала введение коэффициентов трения (усредненных величин), позволивших, в свою очередь, существенно упростить расчеты. Но модели систем управления, построенные на этих приближенных оценках, не позволяют объяснить многие процессы, имеющие место в системах с трением, такие, к примеру, как фрикционные автоколебания или появление волновых деформаций рельсов.

Деформационные изменения в зоне контакта можно учесть за счет введения соответствующей фазовой координаты, такое изменение повысит порядок системы дифференциальных уравнений, описывающих движение системы управления, но при этом позволит связать динамику системы и динамику контакта.

Анализ формирования силы тяги в контакте колеса с поверхностью дороги. Формирование вектора силы тяги в колесном транспорте, в том числе и железнодорожном, происходит в зоне контакта колеса с поверхностью дороги. В железнодорожном транспорте определяют зависимость силы тяги от величины продольного проскальзывания колеса относительно поверхности рельса [1]. Продольное проскальзывание (крип) является разностью между скоростью движения поверхности колеса и скоростью перемещения центра масс колеса относительно поверхности дороги. В условиях чистого качения (по инерции) эти скорости совпадают. Зависимость между тангенциальным усилием и крипом представлена на рис.1 [1].

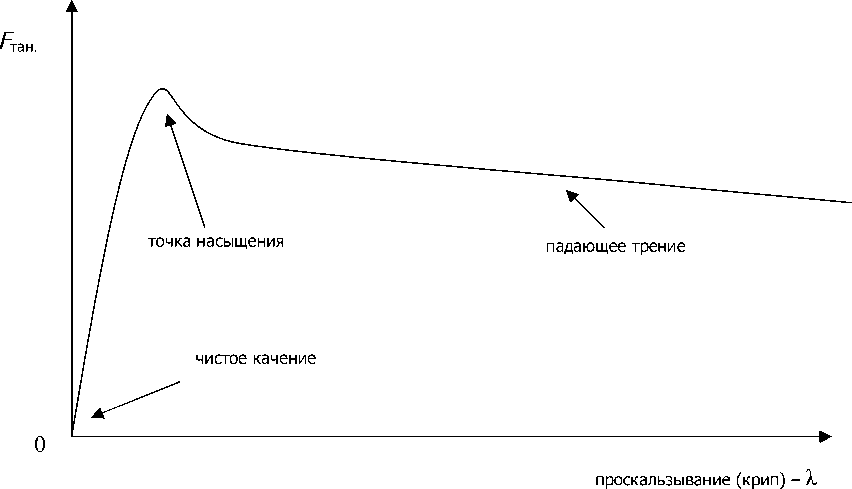
Рис.1. Зависимость тангенциальных усилий от проскальзывания

При анализе данной зависимости возникает закономерный вопрос, откуда берется проскальзывание, чем оно обусловлено? Проскальзывание – явление, связанное с упругими и упругопластинчатыми деформациями в материале дороги (рельса) [2]. Так, анализируя зависимость, представленную на рис.1, можно увидеть, что часть характеристики до точки насыщения является зоной упругих деформаций, точка насыщения характеризует модуль упругости, а часть характеристики за точкой насыщения является зоной упруго-пластинчатой деформации.

Возникновение упруго-пластинчатых деформаций в материале рельса под воздействием тангенциальной силы показано на рис.2.

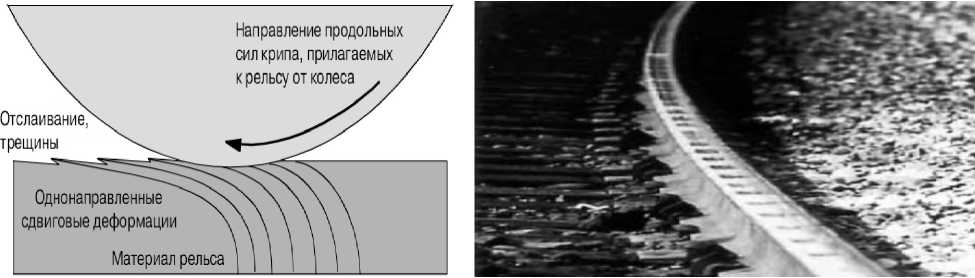
Слои микроструктуры

а )                                                                б )

Рис.2. Возникновение продольного проскальзывания деформаций:

а – рельса в зоне контакта колеса и рельса; б – пути под действием тангенциальной силы.

На представленном рисунке рассмотрен крайний случай, когда тангенциальное усилие превышает модуль упругости. В большинстве случаев, когда движение происходит в зоне действия силы трения сцепления ( F тан . до точки насыщения, см. рис.1), тангенциальное усилие не превышает модуль упругости. В материале рельса под действием тангенциальной силы происходит, с одной стороны, растяжение, а с другой стороны, сжатие материала. Отметим, что в этом процессе участвует только верхняя часть рельса, при этом глубина слоя участвующего в сдвиговых дефор- 1425

мациях определяется степенью деформации колеса и рельса в зоне контакта под воздействием нормальной силы.

Для построения модели тангенциального движения центра масс колеса, необходимо учесть влияние на параметры такого движения динамики деформационных перемещений центра масс под действием нормальной силы.

Модель вертикальных перемещений без учета относительного движения контактирующих поверхностей. Рассмотрим систему, оказывающую влияние на контакт, силу и связанную с ними систему координат, на примере взаимодействия колеса с поверхностью дороги.

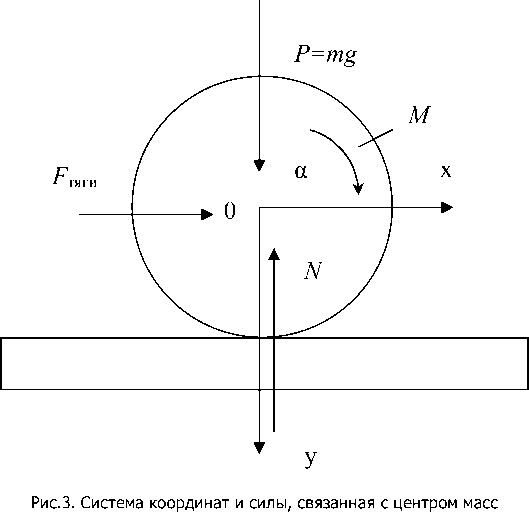
На рис.3 представлено колесо (радиусом R ) и рельс (опора). Силы и моменты, приведенные к центру масс колеса: P – сила тяжести, N – сила реакции опоры, M – внешний вращающий момент, F тяги - сила, вызывающая линейные перемещения центра масс колеса (вдоль оси х ), зависящая от момента M .

Под воздействием силы тяжести P центр масс колеса начнет движение вниз (положительное направление оси y), деформируя колесо и опору, при этом сила, действующая навстречу этому движению N (сила реакции опоры), начнет нарастать, по мере увеличения деформации колеса и опоры (координата y) до тех пор, пока не уравновесит действие силы тяжести. Нам не известны характеристики силы реакции опоры, но известно, что она изменяется от нуля до значения равного силе тяжести и это изменение носит характер, близкий к апериодическому [3], следовательно, будет справедливо следующее равенство:

d ² y dy

P = m ---г- + h. --+ c, y .

dt ^{2       1} dt ^{1 .}

В выражении (1) m - приведенная к контакту масса колеса в кг, h, c – характеристики вязкости и жесткости деформируемого слоя материала рельса и колеса в Н - с/м, Н/м.

Если к колесу приложен внешний вращающий момент (см. рис.3), то возникает вращательное движение и связанное с ним, через трение в контакте колеса и опоры, линейное перемещение центра масс колеса. Не проводя анализ силы трения, оценим влияние этих двух видов движения на деформацию контактирующих поверхностей. Данные, полученные опытным путем [3, 4], показывают, что зависимость деформационных изменений от скорости вращения колеса и линейного перемещения имеет вид близкий к апериодическому, при этом угловая скорость колеса влияет на деформацию зоны контакта колеса, а линейная скорость влияет на деформацию зоны контакта опоры.

Рассмотрим это явление на примере, приведенном на рис.4 [1]. Здесь представлено изменение пятна контакта на рельсе при увеличении относительной скорости скольжения, движение системы происходит на восходящем участке кривой. С увеличением скорости происходит как бы всплывание колеса и пятно контакта существенно уменьшается, при некотором критическом значении сцепление теряется вообще и остается только скольжение.

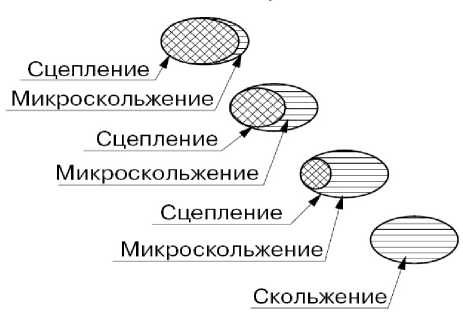
Рис.4. Переход от сцепления к скольжению

В случае значительной деформации опоры и колеса, при наличии линейного перемещения центра масс, колесо движется не только тангенциально (горизонтально), но нормально (вертикально). Вертикальное перемещение центра масс колеса связано с тем, что при движении колеса происходит замена контакта деформированных поверхностей на недеформированные части. Используя предложенный ранее подход по нормировке действующих в зоне контакта сил относительно нормальной нагрузки, вместо выражения (1) получим следующую зависимость:

d a , dx _x

— ( k 3---- + k 4     )

P — P (1 - e ^{dt dt} ) = m

_d 2 _y dt ²

dy

+ h i ^ ' c i y dt

da  dx где dt , dt соответственно угловая и линейная скорости колеса в рад/с, м/с; k3, k4 – коэффи- циенты, зависящие от свойств материалов, из которых состоят колесо и опора.

Предлагаемый подход к моделированию влияния угловой и тангенциальной скорости движения на вертикальные деформационные движения центра масс колеса, похож на действие выталкивающей гидродинамической силы. Следуя таким рассуждениям, центр масс колеса при увеличении скорости движения (угловой и тангенциальной) начинает как бы всплывать, при этом уменьшается деформация контактирующих поверхностей и как следствие этого, уменьшается си- ла трения.

Раскроем в правой части выражения (2) скобки и приведем подобные, получим: ,. d a , dx                 2

^{- ( k 3} '^k4^        d y . dy

Pe ^{dt dt} = m ---— + h + c, y .

dt ¹ dt ^{1 .}

dx  d a a

Для упрощения выражения (3) учтем тот факт, что — = f (—), при этом из геометрии dt dt пR известно, что длина дуги окружности линейно зависит от угла - l = a, а эффект относитель-180

ного проскальзывания контактирующих поверхностей колеса и дороги, в условиях стационарности тяговой характеристики, можно линеаризовать коэффициентом k 5 , значение которого находится между нулем и единицей. Исходя из этого, представим выражение (3) следующим образом:

— k y to

Pe ²

d y dy m---+ h + с, У , dt 1 dt 1 ,

где k _Е ~ к 3 + к 4 к 5

п R

------ го

180 ^,

d а dt

Связь вертикальных деформаций контактирующих поверхностей с тангенциальными силами в зоне контакта. Принято разделять действующую в зоне контакта тангенциальную силу, возникающую в условиях вращательного движения колеса, как совокупность следующих сил:

• –    сила трения сцепления (покоя) F тр.сц. ;

• –    сила трения скольжения F тр.ск. ;

• –    сила трения качения F тр.к. .

Сила трения сцепления характеризует участок кривой, представленной на рис.1, до точки насыщения, сила трения скольжения характеризуется падающим участком этой же кривой. Сила трения качения, имеет различную интерпретацию, но наиболее общим будет высказывание, что трение качения – это потери на продольное движение центра масс при условии, что тангенциальная сила будет находиться на участке до точки насыщения (см. рис.1) [1].

Учет нормального деформационного движения центра масс колеса позволяет легко интерпретировать возникновение потерь при продольном движении центра масс колеса как потери тангенциальной силы, пропорциональные текущему значению нормальной деформации «y» (рис.5).

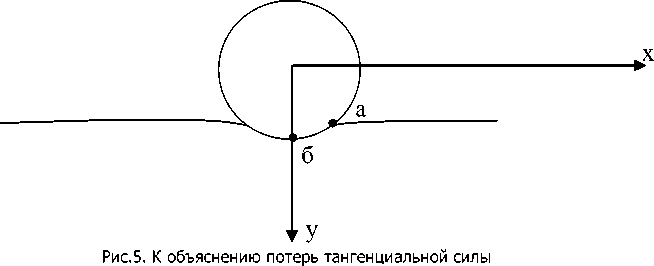
Для того чтобы центр масс колеса начал перемещение вдоль оси х необходимо перенести нормальную нагрузку из точки (б) в точку (а), что требует от тангенциальной силы провести работу, обратную работе нормальной силы по деформации колеса и опоры в точке (б). Иными словами тангенциальная сила должна поднять центр масс колеса вертикально вверх на расстояние y (текущее значение деформационных изменений колеса и опоры).

В предлагаемом подходе к описанию силы трения качения (потерь на продольное движение) нет необходимости разделения тангенциальной силы на силы трения покоя и скольжения. Так как в обоих случаях будут присутствовать «анти – деформационные» потери пропорциональные y . Дифференциальное уравнение, описывающее продольное движение центра масс, будет иметь следующий вид:

dx d ² x dx

Fтяг - yPsign (—) = m -7-Г+ hnp -77, (5) dt dt2 dt где, F - тангенциальная сила, приложенная к центру масс колеса Н, yP s ign ( x ) - потери тяг                                                                         dt тангенциальной силы на преодоление деформационных изменений контактирующих по-dx верхностей Н, sign (   ) - нелинейная функция, связывающая потери на трение качения с dt продольным движением центра масс колеса, m, hпр - параметры, характеризующие инерционные и вязкие свойства продольного движения центра масс колеса.

Тангенциальная сила ( F_тяг ) зависит от текущего значения нормальной деформации контактирующих поверхностей колеса и дороги « y », так как, чем больше деформация, тем сильнее связь контактирующих поверхностей друг с другом. Текущее значение – « y » удобно нормировать относительно максимального, и полученное нормированное значение в дальнейшем использовать как весовой коэффициент при тангенциальной силе:

F = —^—F тяг . n                 таг . тек . ,

y max где y max определяется отношением нормальной силы к значению с 1.

dx

Применение нелинейной функции связи - sign (—) в уравнении (6) обусловлено тем, что dt dx потери на трение качения присутствуют только в случае наличия движения, т.е. если — # 0 . dt dx

Вместе с тем, функция sign крайне неудобна, так как в точке — = 0 она имеет разрыв. Удоб-dt но заменить функцию sign на гиперболический тангенс:

kx - kx i n \ e — e

th (x) =                , kx - kx , e + e где k - коэффициент характеризующий степень близости функций sign (x) и th (x) ,

Lim [ th ( kx )] = sign ( x ) .

k ^ да

Гиперболический тангенс

–

гладкая функция, непрерывная на интервале

x e ( -да , да ) , при этом степень пологости функции вблизи точки ноль определяется значением k.

С учетом предложений и замечаний (6-8) выражение (5) примет следующий вид:

y „           d ,            d ² x . dx

-----^аг.тек. ^- У ^{P th (}~^ = m     ^{+ h} пр "T" • y max                    ^{dt       dt         dt}

Таким образом, выражение (9) описывает линейное продольное движение центра масс колеса в условиях, когда вертикальное движение центра масс под действием нормальной силы описывается выражениями (2), (3).

Возникновение циркуляционных сил в зоне контакта колеса и опоры. На рис.2, б представлен участок железнодорожного пути с продольными деформациями, которые носят колебательный характер. Рассматриваемая модель учета влияния деформационного сближения контактирующих поверхностей колеса и опоры на динамику движения центра масс колеса позволяет достаточно просто (для случая одной массовой системы) объяснить это явление как следствие действия циркуляционных сил. Рассмотрим систему уравнений, описывающих нормальное и тангенциальное движение центра масс колеса в рамках предлагаемого подхода:

<

yF таг. тек. y m ax

Pe

,, d а , dx

⁽ k 3 77Т+ k 4^

dt dt

, dx х      d2 x, dx

- ypth (FF) = m ' dt       dtdt d 2y , dy

= m 7- + h,--+ c, y dt21

.

Реакция системы (10) на изменение координаты «y» вызовет возникновение циркуляционной составляющей вектора силы и как, следствие, процессионное движение центра масс коле- са. Докажем это, проведя анализ матрицы жесткости системы (10). Для начала проведем несколько замен в (10), позволяющих указать связь сил, действующих на систему координат движе- ния

центра масс, получим следующую систему уравнений: d ² x      dx

Fi( У ) = m -Т7Г+ hnp-T-dt        dt d 2 y dy

I F 2 = m dt ⁺ h i d;⁺ c i y

,

• „ , _x y                   _n d.dx_x               - ( k 3 d a₊ k 4 dx )

y _max                      dt ²

Матрица жесткости системы, описываемой уравнениями (11), будет иметь следующий вид:

C =

a f 1 d y c ₁

,

где

^F1- =   — F - Pth d—T)

⁽              таг . тек . t ⁽       )) .

• ^d y     y max                    ^dt

0.5 ^ F i d y

Матрица (12) несимметрична, путем простых преобразований такая матрица превращается в сумму симметричной и косо-симметричной матриц:

C =

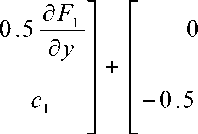
a f 1 d y

dF 0.5 ^ F ¹

d y

.

В выражении (13) первая матрица симметрична относительно главной диагонали и характеризует вертикальную и горизонтальную составляющую сил, действующих в контакте колеса и рельса, а вторая матрица косо-симметрична и характеризует циркуляционные силы, которые, в свою очередь, вызывают волнистые деформации в материале рельса (см. рис.2, б ) Заключение. О существовании деформационных изменений контактирующих поверхностей колеса и опоры известно давно, но учет этих изменений крайне сложная и неоднозначная задача, решаемая многими авторами ранее [3, 4]. Отличие предлагаемой модели от известных [3, 4] состоит в том, что она позволяет связать деформационные изменения в контактирующих поверхностях с основными параметрами движения системы не на каком-то этапе контактного взаимодействия, к примеру, в режиме скольжения, а во всех режимах. Такой подход позволит моделировать движение систем, имеющих фрикционный контакт типа: «колесо-опора» во всем диапазоне изменений фазовых координат.