Модель трафика современных глобальных сетей для системы имитационного моделирования

В течение последних двух десятилетий начиная от известных статей, таких как [1], анализ и моделирование самоподобного трафика очень актуальная тема для теоретических и прикладных исследований. Представленные коллекции теоретических и практических достижений в этой области за последние двадцать лет можно найти в [2]. В настоящее время влияние самоподобного трафика на различные аспекты телекоммуникаций остается важной темой для исследований [3-6].

Важными проблемами в данной области являются разработка относительно простых в анализе моделей трафика и оценка их способности генерировать трафик, близкий к реальному. Первой целью данной статьи является представление собственной модификации известной модели самоподобного трафика «M/G/∞ Input», реализованной в системе моделирования OMNeT.

Модифицированная модель способна воспроизводить несколько характеристик реального трафика WAN сетей одновременно, включая параметр Херста, одномерное распределение вероятностей величин (ОРВВ) и нормированную автокорреляционную функцию (НАКФ) трафика. Потому вторая цель статьи – сделать параметры модифицированной модели «M/G/∞ Input» более интерпретируемыми с практической точки зрения.

Отличие данной работы от хорошо известной статьи [7] в том, что там информационная скорость (ИС) индивидуальных источников (ИИ) предполагалась одинаковой и равной единице. Поэтому ОРВВ трафика, сгенерированного моделью «M/G/∞ Input» (такую модель в данной работе назовем базовой), было пуассоновским, а для последующего приведения к требуемому распределению использовалась преобразовывающая функция. По нашему мнению, недостаток данного подхода в том, что он сталкивается с трудностями трактовки преобразовывающей функции с практической точки зрения. В статье используется другой подход: мы предполагаем, что каждый ИИ может иметь свою собственную ИС, а суперпозиция таких неоднородных ИИ создает соответствующее ОРВВ результирующего трафика. Основные результаты данной работы были представлены на конференции [8].

Статья структурирована следующим образом: во втором разделе произведен обзор базовой модели «M/G/∞ Input» и представлена модификация, которая реализована в программном пакете; в третьем разделе описан программный пакет и предоставлены результаты моделирования трафика, в четвертом разделе подведены итоги и сделаны выводы.

Модель «M/G/∞ Input»

Для простоты будем рассматривать процесс с дискретным временем. Пусть ось времени делится на одинаковые временные интервалы, и размер каждого такого окна будет единицей времени. Также пусть количество информации измеряется в ячейках, а размер одной ячейки в байтах. Таким образом, трафик и ИС источника измеряются в ячейках в одно временное окно. В модели «M/G/∞ Input» число новых ИИ, появляющихся в системе в каждом временном окне, является случайным. Все числа новых ИИ, во всех временных окнах, являются независимыми одинаково распределенными случайными величинами (НОРСВ) с пуассоновским законом распределения с параметром λ.

Известно, что самоподобие моделируемого трафика определяется распределением вероятностей времени жизни ИИ – оно должно быть с тяжелым хвостом. Если время жизни для всех ИИ являются НОРСВ с обозначенной общей случайной величиной T и ее распределение вероятностей удовлетворяет тогда параметр Херста смоделированного трафика по «M/G/∞ Input» равен H. Чтобы сделать АКФ моделируемого трафика похожей на АКФ реального трафика, мы будем использовать следующую функцию распределения вероятностей времени жизни:

рг{У = А-} =

' C(k + xYv™,

к = 1;

£ = 2;3...,    ’ где x и y параметры для минимизации отклонения, C – нормирующая константа. Как показано в [9-10], в случае такой параметризации нормированная АКФ моделируемого трафика имеет вид:

(i-y)£5>+<™

^ =---------------------• (3)

£ bi + хУ^ + (1 - y)^ £ у + хУ^ин'

/7=2                                           /=1 /7 = /‘+1

Имея несколько значений r _k , k = 1; 2 … K , АКФ реального трафика, мы можем сделать АКФ (3) более близкой к реальной, производя минимизацию по x и y среднего квадратичного отклонения

О(х,у) = ^(г(к)-г_кУ.       (4)

k=l

В каждом временном окне в течение всей жизни каждый индивидуальный источник генерирует трафик (некоторое количество ячеек). Сумма потоков от всех активных источников и есть результирующий трафик модели. В базовой модели «M/G/∞ Input» считалось, что все источники имеют одинаковую скорость генерации трафика (информационную скорость). В стационарном состоянии системы величина результирующего трафика Y _t в случайный момент времени t строго пропорциональна числу активных источников N _t в системе в тот же момент и имеет пуассоновское распределение с параметром

L = XEyy           (5)

(E – оператор математического ожидания). Поэтому обозначим pk = Pr{^ = k\ = exp(-Z)ZA !k\; k= 0;l... (6)

Предложенная модификация базовой модели – это предположение, что ИС являются НОРСВ с общим обозначением случайной величиной S . Если в какой-то момент t в системе имеется N _t активных источников, то обозначим их скорости как S , k = 1; 2 … N . kt

Как показано в [9-10], зная распределения вероятностей {Pr{ Y = k }} _{k = 0; 1; 2 …} величин трафика Y , мы можем найти распределение вероятностей случайной величины S , которое обеспечивает данное распределение трафика Y . Опишем эту процедуру с некоторыми пояснениями. Для начала допустим, что

Pr{5 = 0} = 0 .             (7)

Это «условие отсутствия фиктивных источников» обеспечивает ситуацию, что Y_t = 0 тогда и только тогда, когда N_t = 0, поэтому

Рг{У = 0} = _A = e"^L и (8)

L = -Pr{7 = 0}.            (9)

Скорость индивидуального источника S (число ячеек в окно) целочисленная случайная величина, поэтому Y _t = 1 тогда и только тогда, когда N _t = 1 и S ₁ = 1, поэтому

Рг{У = 1}=р, Pr{S = l},       (10)

откуда мы получаем P r { S = 1}. Затем Y _t = 2 тогда и только тогда, когда N _t = 1 и S ₁ = 2 или N _t = 2 и S ₁ + S ₂ = 2 (что значит S ₁ = S ₂ = 1), получаем

Pr{У = 2} =_Л Pr{S = 2} + p, Pr{S, + S, = 2}; (11)

и, зная Pr{ S = 1}, получаем

Pr {^ = 2} = Pr ^ = 2Ь Л (pr {^ = U )2  (12)

P\

В общем случае имеем

W=kV^Lp„^^S=k^

Yr{S^k}^            ^m=2      "⁼¹       , (13)

где

может быть найдена как

m-кратная свертка моментов конечной последовательности {Pr!$ = /)},.„где все эти вероятности известны из предыдущих итераций.

На практике расчет этих сверток является наибо- лее трудоемкой частью итерационной процедуры (7) и имеет экспоненциальную сложность, когда растет k. Из (5) мы можем найти

L = X/E(t\            (14)

В итоге в нашей модели получились интерпретируемые параметры: интенсивность появления новых ИИ ^ распределение вероятностей времени жизни ИИ и распределение вероятностей ИС ИИ.

НАКФ реального и смоделированного трафиков. Для сравнения также приведены ОРВВ и НАКФ трафика, смоделированного по базовой модели «M/G/∞ Input» (все ИС для ИИ равны единице).

Моделирование трафика WAN сети

Представленный программный пакет на базе OMNeT++ доступен по ссылке [12] и называется SelfSimMGI. Его первое назначение – анализ трафика, так как есть возможность сбора статистики о трафике для последующего расчета статистических характеристик и параметра Херста.

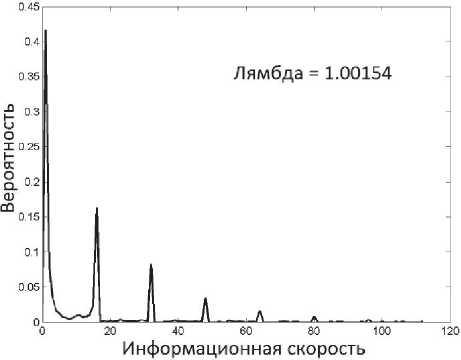
Рис. 1. Распределение вероятностей скорости источника для трассы 1

Определенный модуль читает трафик из файла с трассой, генерирует OMNeT пакеты согласно записям в файле и посылает их в исходящий порт. Другой модуль является сборщиком статистики, он собирает необходимую статистику, анализируя проходящие сквозь него OMNeT пакеты, вычисляет ОРВВ трафика, НАКФ и параметр Херста. Результаты записываются в XML файл.

Вторая цель – моделирование трафика. В пакете имеется модуль-вычислитель параметров, который читает статистику из вышеупомянутого файла, вычисляет параметры «M/G/∞ Input» модели и записывает их в другой XML файл. Генератор трафика читает эти параметры из файла в начале каждого запуска моделирования и генерирует трафик как поток OMNeT пакетов в соответствии с моделью «M/G/∞ Input». Статистические данные смоделированного трафика также собираются вышеупомянутым сборщиком статистики.

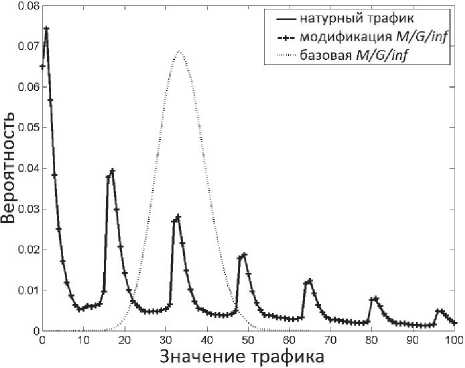
Рис. 2. Распределение вероятностей трафика для трассы 1

В данной работе приведены результаты экспериментов на основе трех трасс из коллекции CAIDA [11]. Трассы 1 и 2 – одноминутные, записанные монитором equinix-chicago в двух противоположных направлениях: A и B. Они записаны 19. 12. 2013 г. в 13:00. Трасса 3 той же длительности, но записана монитором equinix-sanjose 20. 11. 2008 г. в 13:00. Обработка этих трасс была сделана с использованием временного окна равного 15 мкс и размером ячейки равным 100 байтам. Размер ячейки определяется из требуемой точности представленного трафика, а размер временного окна – из соображений вычисления параметров модели за умеренное время. Наиболее трудоемкая операция — это вычисление сверток в (13).

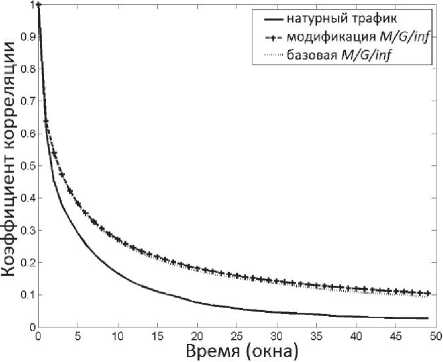
Рис. 3. Нормированная АКФ для трассы 1

Результаты о способности модельного трафика аппроксимировать реальный трафик представлены в графическом виде – некоторые количественные данные о способности аппроксимации модели см. в [10]. Для всех трасс представлено распределение вероятностей ИС ИИ и интенсивность появления новых ИИ X, а также ОРВВ и

Интересно, что все распределения вероятностей ИС являются мультимодальными, и это обеспечивает очень хорошую аппроксимацию ОРВВ реального трафика, которое также мультимодальное. На рис. 5 отмечен интересный артефакт в ОРВВ реальной трассы вблизи значения 150-200 (ячеек на слот).

Принимая во внимание, что вблизи отметки 200 ячеек в окно на оси x (см. рис. 5) величина реального трафика составляет около 10 Гбит/с, то очевидно, что линия связи в этот момент была загружена почти на 100%, и система управления потоком начала ограничивать трафик (см. [6] для описания сетевого оборудования). Наша модель пока не обрабатывает такую ситуацию.

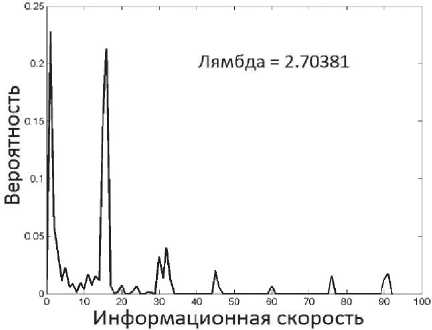
Рис. 4. Распределение вероятностей скорости источника для трассы 2

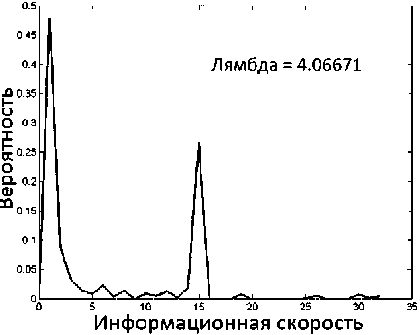
Рис. 7. Распределение вероятностей скорости источника для трассы 3

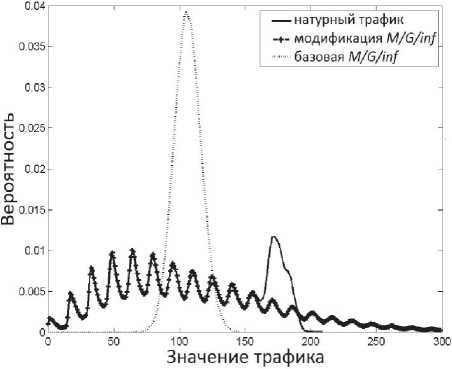
Рис. 5. Распределение вероятностей трафика для трассы 2

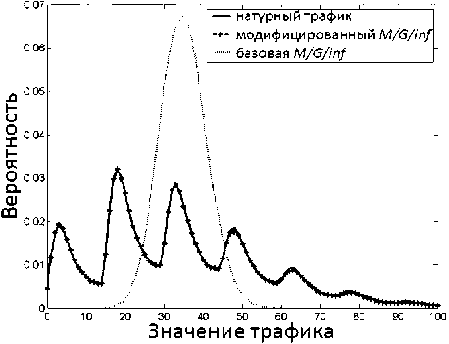
Рис. 8. Распределение вероятностей трафика для трассы 3

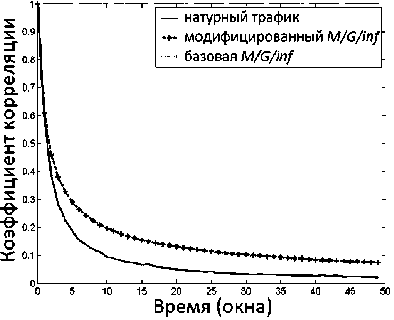
Рис. 6. Нормированная АКФ для трассы 2

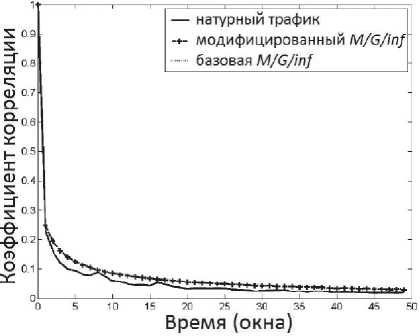
Рис. 9. Нормированная АКФ для трассы 3

Как мы видим, мультимодальное поведение распределения вероятностей трафика часто происходит в трафике WAN сетей в течение последних двух десятилетий, однако интенсивность трафика выросла значительно за этот период времени. Значения параметров Херста для всех трасс представлены в таблице 1: видно, что самоподоб-ность и корреляция достаточно хорошо воспроизводятся предложенной моделью «M/G/∞ Input».

Таблица 1. Значения параметра Херста

Трасса	Параметр Херста
	Реальная трасса	Модификация M/G/cc	Базовая M/GM
Трасса 1	0,66	0,75	0,74
Трасса 2	0,71	0,73	0,70
Трасса 3	0,70	0,71	0,72

Заключение

Представлены совокупность экспериментальных результатов, полученных с помощью программного пакета SelfSimMGI на базе OMNeT, для анализа трафика WAN сетей и моделирования. В модели получились хорошо интерпретируемые параметры. Обработка реальных трасс этой программой показывает интересный феномен мультимодального «пилообразного» вида у распределения вероятностей современного трафика WAN сетей. Причина такого поведения требует более глубокого исследования и понимания.