Модель турбулентности k - в задаче пограничного слоя на вращающихся телах

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим пограничный слой при осевом обтекании осесимметричного тела, вращающегося вокруг оси симметрии. Координата x измеряется вдоль направляющей тела вращения, y - направлена по нормали к поверхности тела, z - окружная координата (рис. 1).

Пограничный слой подчиняется уравнению неразрывности, а также уравнениям импульсов в продольном и меридиональном направлениях [2].

S V, V dR 5 V _м

—- + ^x   + —- = 0,

5 x   R dx   9y

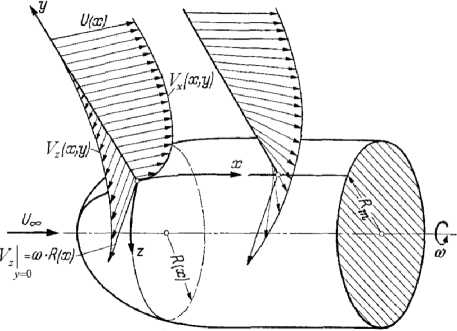
Рис. 1. Схема обтекания жидкостью вращающегося осесимметричного тела [1]

• V d V. — V 2 dR + V V = .d +1 Т. ,_w ^x 9x   R dx ^y 9y     dx p d y

„ 5 V  VV dR „ 5 V  1 Т

• V_x + x^ + V,^ = z ,

5 x R dx ^y 9y    p 9y

мой жидкости уравнения модели k — e могут быть представлены в виде:

где Vx,Vy,Vz– компоненты вектора скорости жидкости, U (x) - скорость внешнего (невязкого) обтекания тела, R (x) - радиус тела враще- d Vx          9 Vz ния, т = Ц--, Т = Ц-- - касательные

’ xy z dy     zy dy напряжения между слоями жидкости. Вязкость ц определяется как сумма молекулярной Ц и турбулентной pt вязкостей.

Модель k — e добавляет в систему еще два уравнения – кинетической энергии турбулентности K и диссипации турбулентности E [3]. В случае тонкого пограничного слоя несжимае-

9K   9K  d

V — + V — = — dx   ^y dy dy

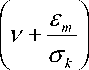
dK

9y

+

+e

m

f^V,+rsV, I2 I yy J I dy J

V aE + V a_E = a.

x 9x    y

E

⁺ c e l K ^e m

—

E ;

9 E

yy 6y LI    ^ e J 6y

fdK)2+fdT YI yy J I dy J

+

E ²

ц       ц K²

где v = —, em = — = сц , параметры p      p  ц E c^ = 0.09, cEX = 1.44, сй = 1.92, ^ = 1, ^ = 1.3. e                   о e                                  e

Прилипание жидкости к телу вращения вместе с известным законом невязкого обтекания определяет граничные условия:

.у - 0: Vx = V, = 0, V. - R®, уу - у, : Vx - U (x), V. = 0, где ye – толщина пограничного слоя.

Модель k — 8 имеет вычислительные особенности на границе у - 0 . Поэтому граничные условия для нее задаются на внешней границе и на границе, расположенной на некотором расстоянии у 0 от поверхности тела. Учитывая это, граничные условия для уравнений к — 8 модели турбулентности можно записать в виде:

k(x,7)-Цу K(x,у), 8(x,7)-Ux3E(x,у), k7 = 5,

8 ^- q ,

( b ₂ 5 ) _n + mfs + e m [ v ² + Q ² p ² ]— 8 — 2 m 2 uk -

^{- x} ( ^ukx ^{— sf}x ) ,

( ^b 3 q ) 7 ⁺ m i ^f q ⁺ c 8i 8 ⁸ m + [ v ^{2 + q 2} p ² ] ^—

^{— c} 8 г k ^— ( ³ m 2 ^{— 1} ) ^{u 8 - x} ( ^{u 8} x ^— qf x ) .

^{у у} 0 ^: E 0 ( ⁸ m ) cs

(д V_x f (д V_z ) ² x ₊ z

I ^d у J 0 I ^d у J 0

Граничные условия системы примут вид:

7 - 0: f - 0, u - 0,           g - 1;

L (⁸ m ) CS

K 0 - Л E 0          ;

У      c —

_: dK_{e -} - E e dE e _{- —}      E e

' dx     U ( x )’ dx      ^{8 2} K_eU ( x ) ,

7 ^- 7 ₀:   ^{8 -} ( ⁸ ,+ ) CS [ v ^{2 +} Q ² p ² ] ,

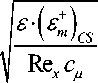
где ( 8 m )_r„ - — - турбулентная вязкость, оп- CS p

7-7e: u -1, g-0,  x—+ 8+2m2k-0, dx

ределяемая в пристенной области у е [ 0, у 0 ] по какому либо альтернативному закону турбулентности, к примеру по модернизированным формулам модели Себеси-Смита [4].

x --+ c.,

8 2 d x

-+⁽³ m 2 I:

8 - 0.

В этих уравнениях введены обозначения:

2. МАТРИЧНЫЙ ВИД УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ

®R b-1+8m,Q - uj ’

U ' m₉ - —x , 2 U

R' m. - —x , 3 R

Вводя функцию тока / ( x , у ) , безразмерную переменную типа переменой Блазиуса

7 - V\U / vx и представляя / - R ( x ) JixU x ) f ( x , 7 ) , V -® Rg ( x , 7 ) , систему (1) приводим к виду [4]:

m , + 1 m ₁ - m ₃ +—2 2—

, ^Re _x ^- —, безразмерная тур

-

булентная вязкость 8 _m ⁺ в пристенной области вычисляется по алгебраическим соотношениям

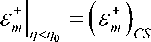
⁽ 8 . ) cs v

, а при 7 >  7 0 исполь

^{u -} f n ,      v ^- / 77 ,       P ^- g n -    (3)

зуется соотношение модели k — 8 :

(bv)n + mfv + m2 (1 — u2) + m.Q’g2 -- x(uux — vfx), (4)(bp ^ + mfp — 2 m3 ug - x (ugx — pfx).

где f , g - безразмерные функции. Нижние индексы 7 и x обозначают дифференцирование по соответствующим переменным.

Уравнения турбулентности можно представить в безразмерном виде, записывая, :

8+ - c Re — m — x 8

Разделение пограничного слоя на пристенную область, в которой турбулентная вязкость описывается алгебраической моделью, и область, где реализуется k — 8 модель турбулентности, удобно проводить, вводя дополнительную переменную, характеризующую коэффициент сопротивления трения на стенке. Такой подход, к примеру, предложен Себеси [3]. Границу 70 выберем исходя из постоянства вели- чины У0+ = 0 т = 50 , где ит = w0U (x) . Для определения п^важно значение w на стенке твердого тела ( Wo ), остальные значения не рассмат- риваются, а производная w по толщине пограничного слоя считается равной 0 (wn = 0) . Величина w0 может быть добавлена в список

V v o + ^{q 2} p 2

переменных модели в виде w _o =--- r 1/4--

, а

граница n ₀ в таком случае рассчитывается как

П о = У о ⁺

w ₀ Re _x ^.

8 j = \5f_j S u j S v j 5 g j S p j S k j 5 s j Se j S q j S w J, j = 0,..., J .

Блоки A , B , C – матрицы размером 10 х 10, блоки r - матрицы 10 х 1. Матрицы разрежены. Значения их ненулевых элементов приведены в Приложении.

Для начала работы итерационного метода приближений требуется задания начальных профилей используемых переменных. Начальные профили f , u , v , g , p могут быть определены как начальные профили для ламинарного течения [4]. Профили же k, s, e , q можно задать следующим образом:

Система уравнений в частных производных решается методом сеток с использованием конечно-разностной схемы “прямоугольник”. Получившиеся нелинейные уравнения линеаризуются по Ньютону [5]. Следующая итерация переменных f , u , v , g , p , k , s , г , q , w находится в виде: f i ⁺ 1 = f i + S f j .

Итоговую систему линейных алгебраических уравнений представим в матричном виде:

Aδ =r .                 (7)

Матрица коэффициентов системы (7) имеет блочную трехдиагональную структуру:

k = ^2^ Iv ² + _Q 2 pp a ₁ Re _x               ^,

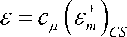
v ² + Q ² p²

a 1 ^{2        ,}

s = k n , q = ^e n .

3. ПРИМЕРЫ РАСЧЕТА И СРАВНЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

A 0 C 0

B 1 A 1 C 1

B j A j C j

B j - i A j - i C j - i

B _J A _J

Векторы переменных

δ 0 δ 1

r ₀

r ₁

8 = 8

8 j - i δ J

rj-i rJ

Реализация предложенной модели проведена в системе MATLAB в модернизированной программе Vertel.

Результаты расчета для тела Парра [1] при Q = l,...,4 и Re = 3 • I0 5 ...9 - 10 5 представлены на рис. 2, 3. Сравнение рассчитанных профилей пограничного слоя с данными эксперимента [1] показывает хорошее соответствие.

Сравнение толщины вытеснения импульса

ye

O x = j u ( l - u ) dy

на рис. 4 и коэффициента мо-

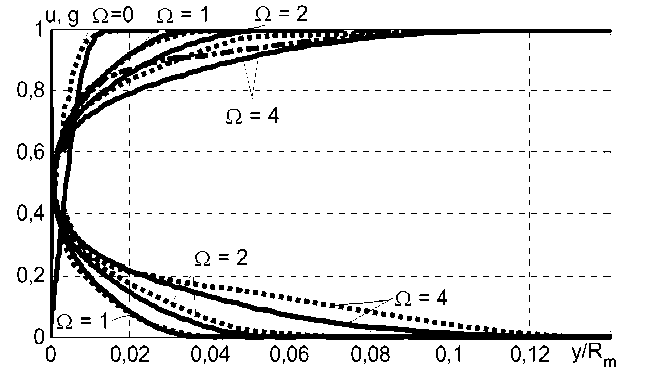
Рис. 2. Сравнение безразмерных профилей меридиональной u и окружной g компонент скорости пограничного слоя при различных скоростях вращения Q , Re = 3 - l0 ⁵ , x / R _m = 3,l . Сплошная линия – расчеты, пунктир – эксперимент Парра [1]

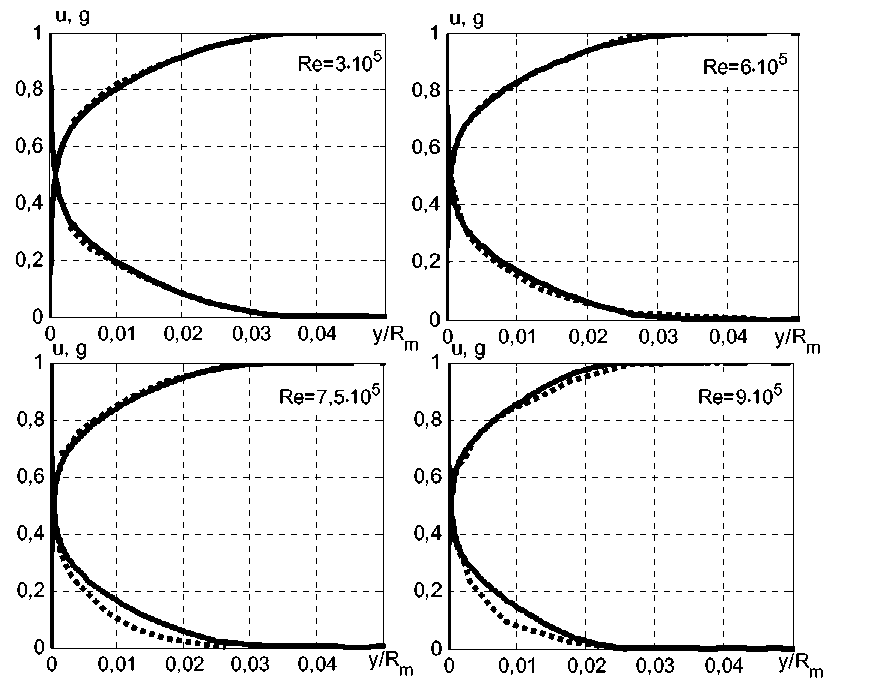
Рис. 3. Сравнение безразмерных профилей меридиональной u и окружной g компонент скорости пограничного слоя при различных числах Рейнольдса, Ω = 1 , x / R _m = 3,1 . Сплошная линия – расчеты, пунктир – эксперимент Парра [1]

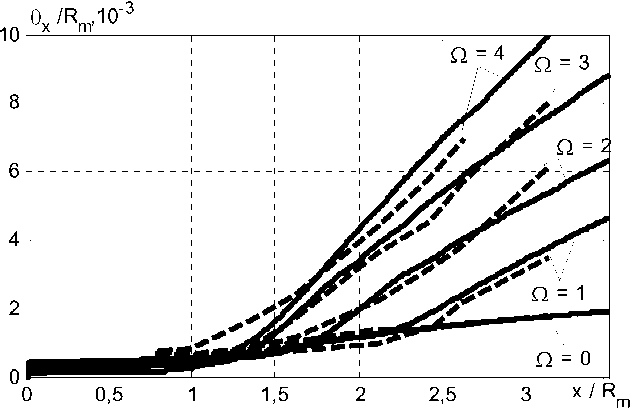
Рис. 4. Сравнение толщины вытеснения импульса в меридиональном направлении, Re = 3 ⋅ 10 ⁵ , x / R _m = 3,1 . Сплошная линия – расчеты, пунктир – эксперимент Парра [1]

мента силы трения в окружном направлении

C M

M

• 1         на рис. 5 также показывают хо-

• 2    ρ Ω ² R _m ⁵

рошее соответствие расчета и результатов эксперимента.

Хорошее соответствие результатов эксперимента Лутандера-Ридберга [2] по исследованию положения точки отрыва потока на вращающемся в осевом направлении шаре при Re ⁼ 1, 6 ^⋅ 10 с результатами моделирования (рис. 6) подтверждает возможность использования описанной модели и ее программной реализации в системе

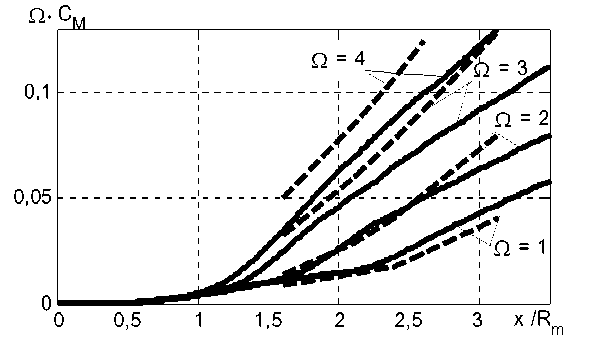
Рис. 5. Сравнение коэффициента момента трения в окружном направлении, Re = 3 - 10 5 . Сплошная линия – расчеты, пунктир – эксперимент Парра [1]

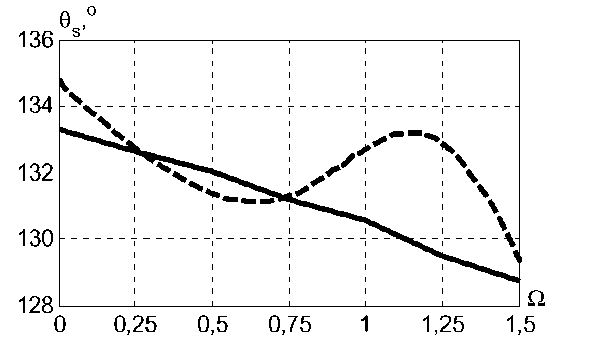
Рис. 6. Сравнение положения точки отрыва потока на вращающемся шаре: сплошная линия – расчет, пунктир – эксперимент Лутандера-Ридберга [2]

MATLAB для нахождения точек отрыва потока в задачах вращающихся осесимметричных тел в осевом потоке.

4. ВЫВОДЫ

Модель турбулентности k - ε представлена в форме, предназначенной для описания осесимметричного пограничного слоя на вращающихся телах, и реализована в системе MATLAB. Сравнение результатов расчета по этой модели с данными экспериментов Парра и Лутандера-Ридбер-га показывает хорошее соответствие, что позволяет использовать модель турбулентности для решения задач пограничного слоя на вращающихся телах, в том числе до точки отрыва потока.

ПРИЛОЖЕНИЕ.

КОЭФФИЦИЕНТЫ ЛИНЕАРИЗОВАННЫХ УРАВНЕНИЙ ТУРБУЛЕНТНОСТИ

Коэффициенты зависят от значения координаты η _j , определяющей положение точки сетки на толщине пограничного слоя.

Элементы матриц A ₀, C ₀ и r ₀ , определим из условий на поверхности тела вращения:

1,1        2,2        3,4          5,2          6,47,6

A 0 = A 0 = A 0 = A 0 = A 0 = A 0 =

8,7          9,810,9

A0    A0    A0

A 5, ³ = A 0, ³ = - h i /2, A 4, ³ = 2 v 0 , A 4, ⁵ = 2П³ Р 0 ,

A c' ⁵ = - 4 Re . ^.

5,2       6,4       7,6       8,7       9,810,9

C0    C0    C0    C0    C0    C0

C 0 ^,3 = C 0 ^,5 = - h i /2.

^r 0 ⁴ = ^Re x w — ^v 2 — ^ 2 P 02 , ^r 05 = ^{( r} 4 ) e , ^r 06 = ^{( r} 5 X .

Уравнения импульсов задаются одинаково при всех j = 1,..., J , поэтому первые 4 строки матриц A j , B j , C j и r _j будут одинаковы во всех областях пограничного слоя:

A '³» = A» = 1,   A“ = - h j /2,   A 3⁴ = ( » з ) j ,

A 3" = ( » 5 ) j ,A 3³ = ( ^ i ) j , A» = ( » 7 ) j ,

A j '= ( в з ) j ,A 4² = ( в 5 ) j . A« = ( 0 9 ) j .

A 4" = ( в '   A = ( в j B   — B j ' — - 1,

B 2'² — - A , /2, ^B3^J = ⁽ $ 4 j ^{B — (} $ 6 j

B   = ( $ 2 AB ^; = ( $ 8 j B 4 A j

r 80 ^{— (} r 5 j , r 90 ^{— (} r dk j , r j 0 ^{— (} r de j ,

где D 1 ^{— g}_js — d v

^{j 0} 5 p ⁽ m ) CS ,

B' = ( в ) , B ⁴ = ( P 10 ) , , B" = ( e j

B 4 = ( в ) , . r = 0, j = ( Г 1 ) , , / = ( r ) , ,

^r4 — ( ^r ₃ ) j., первые четыре строки матриц C , -

нулевые.

^{( r} i ) ,-, ^{( r} 5 ⁾ _j , а также ⁽ $ 1 ⁾ _j ,-, ⁽ $ 8^ , ( А ) j ,..., ( ^в 10 ) , соответствуют коэффициентам линеаризации уравнений импульсов в меридиональном и окружном направлениях [4].

Задание модели турбулентности в различных областях пограничного слоя приводит к определению нижних шести строк матриц A , B , C , r в каждой из областей отдельно:

- пристенная область, в которой турбулентность описывается алгебраической моделью,

D 3 —- 2Re _x c , k j 0 , D 4 ^— ( g m ) _CS ,

D ₅ — 2Re x c ^ k j ₀ V j 0 , D ₆ — 2Re , c ^ k 2₀ П ² P j 0 , D 7 — 2Re x c _M k j 0 [ v 20 + П ² p 200 ] , D 8 — - 2 g j ₀ ,

^{( r}D 1 ) j 0 ^{— Re} x ^cn^kj 0 ^{- (g} m ) _CS⁸j 0

^{( r}D 2 ) j 0    ^g j 0

^Re x c M^kj 0 [ v j 0 ⁺ ^ P j 0 ] .

- область пограничного слоя с k - £ моделью турбулентности, j — j ₀ + 1,..., J - 1 :

A ^7,2 _— a ^8,4 _— A ^9,6 _— A ^10,8 _—

A ^7,3 _— a ^8,5 _— A ^9,7 _— A ^10,9 _—

_

_

1,

■ h j+ 1 /2 ;

j ^— V-j ^{- 1 :}

^A 5’ k ^— ( « 2 k - 1 ) j , a , k ^— ( ^ 2 k -1 ) _y ,

B jk ^—( ^ 2 k ^B y k ^—( « 2 kj k — 1,...,9 ;

A ^5,2 _— a ^6,4 _— a ^7,6 _— a ^8,7

— A9’8

— A j ⁰’⁹ —

^{- 1,}

C

A 5;³ — A ■ — A ⁷⁷ — a9’⁹ — - h , + 1 /2, ,

C

7,3

■j

7,2 j

— C

C

¹8'⁵— C 9 ⁷— C j ^0,9 — - h j + 1 /2 ,

' 8"— C 9,6 — C^⁷ — 1,r 5 — ( Г к ) j ,

C ⁵/ — C" — C” — C j — - h + 1 /2 , r j I r /,

5 2 C

6 4

^{— C} j

— C j — C j⁷ — C⁹’⁸ — C j ⁰-⁹ — 1 ,

r j ^{— (} r E )p r j ⁰ — ( r de ) j ,

r 7 ^—( r 4\,  r j ^—( r 5 \, r J ^{— (} r dk )_p

где коэффициенты уравнения k :

r j ^{— ( r}5 ) j r j ^{— (} r dk \■ , r / ^{— (} r de ^' , коэффициен-

ты матриц нижних шести строк B _j нулевые,

⁽ « 1 ) j

( r dk ) _{j -} 1 ^{— k}j- 1 - ^kj ⁺ h j S jA Q

n mA   n x n 0(0f )

—     $ ” + $ ”

2 j 2 j ^1/2 5 f (5 x j

⁽ r de ) j _- 1    ⁸j - 1    ^£ j ^{+ h}j q j - 1/2 .

⁽ « 2 ) j

n m,   „ x „ didf 1

$ j - 1 ⁺      $ j - 1/2 - 4, I I

2        2 dj V dx ) • 1

- граница между различными моделями турбулентности j — j 0 . На этом слое матрица B j ₀ вычисляется по правилам пристенной области, матрица C _{j 0} вычисляется по правилам для области пограничного слоя с k - g моделью турбулентности, а 5-10 строки матриц A _{j 0} и r _{j 0} имеют вид:

^(а з ) j

⁽ « 4 ⁾ j

A

7,2 j 0

8,4

^A j 0

9,6

^A j 0

10,8

^A j 0

^{- 1,}

7,3       8,5       9,710,9

^A j 0    ^A j 0    ^A j 0    ^A j 0      h j + 1 / ²,

5,3              5,5               5,65,8

A j 0   D1, A j 0   D2, A j 0   D3 , A j 0

6,3              6,5               6,66,8

A j 0   D5 , A j 0   D6 , A j 0   D7 , A j 0   D8

⁽ « 5 ) j

⁽ « 9 ⁾ j

n 1 n

- m ₂ k j

- m n k n - 1

^r 50 ^{— ( r}D 1 j ,

r j 0 ^{— (} r D 2 j ,

' 0 ^{— ( r} 4 ) ₇ 0 ,

x ( d k I

2 1 dr ¹

² ( ^d x / j - 1/2

n x ( dk I

2 ¹ dr ¹

² ( ^d x / j - 1/2

1 ( 5 P I ” _{( A} 1 ( 5 P I ”

—          , ( a ) —

2 (d v ), ^V 6’ j 2 (d v ) _-х

^{1 (d} P ¹

2 (5 P j

^{( a} 10 ) j

^{1 (d} P )

² ( ^d P ⁾ j - 1

^{( а} 11 ) j

h j15

n

с b 2

n

д P

n

8 к

с к

n m ₂ u

n

⁽Ф 3 ^

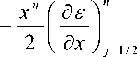
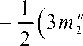
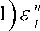
		-	1 (^ Q 2 " 2 ( д к Jj	x n - 2	u "    -д-Г j -1/2 д к (
( а 12	) j =	- h5 n - 1	( d b 2 2 " ( к J j - 1	1 ( + - 2 (	d p 2 n _ a k J j -1
	- m 2 n	" - 1 ( j -1 2 (	■ 8 Q 2 " - . ak J j _ i	x n u 2	n A(‘ j -1/2 дк ( <
( а 13	)q =	h - ( b 2 ) "	n + m^ f n 2 j	xn + — 2	m f 2 " 1 /^ Y I ( ил J j - 1/2
( а 14	) j =	n mn - h / ( b 2 ) j - i + "у		ru +	H xn fa r 2 2 (д x J

n

,

,

1/2

^{( a} i5 ) ,-

с к

д x

Л n ''2n+ 1 f5P2 n J9Q2 s

( де Jj 2 [( де J j ( де J

n

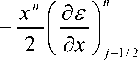
- 2 ( 3 m ■ - ¹ ) ^е , - ,

^{( ф} 4 ) j

( Ф 5 ) j	= 1( 2 1	(д Р _ 2 " ( д v J j ’	( ф б ) j = 2 (	■ д p x 2 n . av J j - 1
( Ф 9 ) j	= 1| 2 1	д р _ 2 " ( ap J j ’	( Ф 10 ) j = 2	(дА 2 ■ ( д p J j -

n

⁽ Ф 11 ⁾ j

- 1q" l^ b ^ h ^j q j ( д к

( d P₁ 2 n ( д к J j

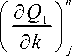
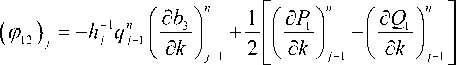
⁽ ^ 15 ) j

^{( a} i6 ) j

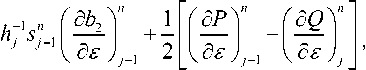
( « 7 ) j   ( « 8 ) j   ( « 17 ) j   ( « 18 ) j   ⁰ >

-, „ (дь3 2n 1 (дq, 2n hq j j (де J j 2 ( де J j

- 2 ( 3 m n -1 ) u n

_ x n n ^(д е 2

2 u j ^{- 1/2} д е (д x J

⁽ r K ) j = -[⁽ b 2 ⁵ ) ■ - ⁽ b 2 ⁵ ) n - i ] h r -

- [ ^1/2 - Q n - i/2 - ² m ■ ( uk ) n - 1/2 + m i n ( f5 ) n - 1/2 ] +

⁽ ^ is ) j

,-i „ (дь3 2n      1 (дq 12n j qj-11 I - I I

( д е J j _ ,    2 ( д е J j - ,

⁺ x n u n - 1/2

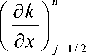
n

⁵ j - 1/2

I f J n 2, (^д x J j - 1/2 J

-2 ( 3 m n -1 ) и " - ,

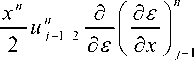
b 2 = 1 +£ = 1 + ^c_^ Re x k ² , P = Re ^k Г v 2 + _M p 2 1 , о к       ° -      е ’ ^{Ц x} е ^{[          ]} ’

⁽ ^ 17 ) j

n

= h j -* ( b 3 ) " + m |^L f j”

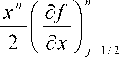
„      db₂   c ^     2 к   д b₂   с _ц      - к ²

Q = £, ~= = ~ Rex —,   = ~ Rex — , дк   ак     е   д е   ок     е

( ^ 18 \

-

h j ¹ ( b 3 ) " - ,

+ m " f " . + x 2 ( f 2 n

2 j ^{1 - 1}     2 (д x J j - ,/2

^Q = = 1, ^{д р} = 2 с Re - Г v ² + П ² p ² ], д е        дк ^{Ц x} е ^{[            ]}’

⁽Ф 7 ) j =⁽ № ) j = ( ^ 13 ) j = ( ^ 14 ) j = ⁰ ,

д p

---= с д е    Ц

Re x е ² [ v 2

+ п ² p ² ] ,

( Г е ) , = -[ ( b 3 q ) n - ( b 3 q ) " - , ] h J '-[ ( P , ) ■ _„ , -

д Pop- 2 — = 2с„ Re, —v , д v Ц x е ’ уравнение е:

— = 2с Re, — П2p

Ц x                а дp          е

е

^{- ( Q} , ) " - 1/2 ^{+ m} n ^{( f} q ) " - ,,. ^{- ( 3 m} n ^{- 1 ) ( и е} ) " - 1,2 ]⁺

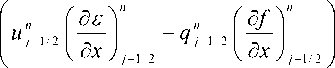
m ⁿ

( Ф ) j = -q q j 2

x ⁿ

q n - 1/2

Ar f 2 n д f (д x J j

г⁺        с

b 3 = 1 + -m = 1 + ^ Re сте         ct-

k ²

е

mn ф )j =    qj-1

ⁿ x_n 2 ^qj - 1/2

A( f ² n д f (д x j

^P i = ^с - 1 ^с ц ^Re x^k [ ^{v 2 + п} 2 p ² ] , ^Q 1

_ е ^{2 с} е 2 , , k

'Q — 2 c L 5 Q _— - _c £

Be       ^{e 2} k ' 8k       ^{e 2} k¹

⁽ r E 2 ) J

d e ) ”         ^{( e} JN ) / „ x „

— + c ?--+ (3 m? — 1) e T ax) J e 2 kJ      ( 2 ) J cP dP

— 0, — = 2 cC Re. kv,

,                  £ 1 Ц X , de     d v

Вычисление производных проводится по

—¹ = 2 c_£Xc Re.,. k Q ² p о 1 Lt        X                 ,

5 p

схеме

(f} ( d x J

A 1 f n ^—2 + A 2 f n ^—1 + A 3 f n , где в

случае использования первого порядка A 1 — 0 ,

— — c_£Xc Re.,. Г v ² + Q ² p ² 1 d k ^{о 1 ц} . _             J .

A 2 —---—, A 3 — x„ — x„—1

, в случае второго ■ n ^{— x}n — 1

- внешняя граница пограничного слоя, j — J . B J в таком случае может быть вычислена по правилам для основной части пограничного слоя, матрицы же A _J и r _J примут вид: A jk ^— ( « 2 k - 1 ) . , A jk ^— ( ^ 2 k - 1 ) . , k — 1,..., 9 ;

порядка A 1 —

^xn ^{— x}n — 1

( ^xn — 2 ^{— x}n — 1 )( ^xn — 2 ^{— x}n ) ,

A — .\ ■ — 1, A J ,6 — E 1 , A J ,8 — e 2 , Aw — E 3 ,

A J ⁰’⁸ = E 4 , Г 5 = ( r K ) j , Г 6 = ( r _E ) j , Г 7 = 0,

J = 0 , Г 9 = ( r E 1 ) j , J = ( r E 2 ) j ,

^xn ^{— x}n — 2

( ^xn — 1 ^{— x}n — 2 )( ^xn — 1 ^{— x}n ) ,

^{2 x}n ^{— x}n — 1 ^{— x}n — 2

( ^xn ^{— x}n — 2 )( ^xn ^{— x}n — 1 ) ,

причем производные вида

"A(d f _)!

_ a f (d x J_ .

— A 3 .

_n „ 5 (5 k ) n где E = 2 mn + xn — — , ^{1      2}       5 k Vdx) j

( e n ) 2 ^J

^E 3       c o 2 , _x2

( J

E 2 = 1,

n Й n 5 (de ) n       2 e J

Ед — (3 m^ — 11 + x — — + c ---

^{4 ( 2}     ) de u x ) J ^{0 2} k J ,

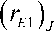
< dkY xn l^k I + eJ + 2mnkJ (5x ) J