Модель управления запасами, определение оптимального размера заказа

Рассмотрим модель определения оптимального размера заказа в условиях определенности. В данном случае заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью, пока не достигнет нуля (рис.1).

В нижней точке графика должен поступить заказ, размер которого

X – размер заказа;

X оптимальный размер заказа;

—

T – протяженность периода планирования.

цикла.

D         X

ТСХ=-О(1); ТСт=-Н(2);

Л             2

равен X, и уровень запасов восстановится              до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период (рис.1 – запас пополняется мгновенно,     убывает     с постоянной интенсивностью).

Производителю необходимо       определить минимальные     суммарные затраты на покупку и хранение средств          производства.

Определим оптимальное число заказов за период и время

d = D(3); Й = Н<4),

где D – величина спроса за период планирования; О – издержки заказа; d – величина спроса в единицу времени (3); H – удельные издержки за период; h – удельные издержки хранения за единицу времени (4); TCx – совокупные издержки заказа (1); TCT – совокупные издержки хранения (2).

Тогда, оптимальное число заказов за период:   W=—(5);

х *

Время цикла (оптимальное время между заказами): t = — = — (6).

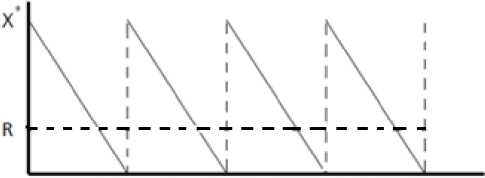
Рассмотрим модель оптимального размера заказа в предположении, что получение заказа не мгновенно (рис. 2). Из условий модели следует, что требуется найти объем запасов, при котором необходимо делать новый заказ.

Введем предположение, что размер заказа может быть получен не мгновенно, а с течением времени. Тогда производителю необходимо заранее делать заказ, чтобы в нужное время иметь достаточное количество товара на складе, а значит, необходимо рассчитать такой уровень запасов, при котором

Экономика и социум №2(15) 2015

Рис. 2. Модель отимального размера запаса при условии, что получение заказа не мгновенно

делается новый заказ. Этот уровень является точкой восстановления R. Пусть L – время выполнения заказа. Тогда точка восстановления будет определяться произведением величины спроса в единицу времени и временем выполнения заказа: R = d х L (7).

В предыдущих моделях допускалось, что пополнение запаса происходит единовременно. Но в некоторых случаях, особенно в промышленном производстве, для комплектования партии товаров требуется значительное время, а производство товаров для пополнения запасов

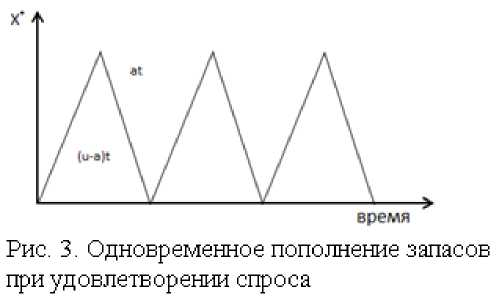
происходит одновременно с удовлетворением спроса. Графическая интерпретация данной ситуации представлена на рисунке 3.

Предположим, что u – уровень производства в единицу времени t; K – фиксированные издержки хранения; K*– совокупные издержки хранения.

Получим выражение для K* (8).

К- = ХтШхН =^(1-1^ (8),   где ХтИ = ^ (9),

Х t = -(10) и

для расчета

2     и                          2

Тогда, издержки заказа:

D

О = -К(11).

Х

Используя формулы 8-11, получим выражение оптимального размера заказа с учетом дефицита:

2D0      d    2D0      d

Х'=]—х(1-и) = ]—х(1-и)(12^.

=^Х ' (¹- ^ )⁽¹³).

Максимальный уровень запасов:5 -_пах

Следует отметить, что при построении модели управления запасами необходимо учитывать как специфику компании, так и ограничения, обусловленные реалиями российской экономики. Однако никакая модель не может быть полным отражением действительности, поэтому менеджерам, принимающим решения, нужно не только знать формулы, но и системно понимать процессы, которыми они управляют. Помимо расчета оптимального размера поставки каждое предприятие должно учитывать свою специфику. Рассмотрим опыт использования данных моделей на примере крупной российской компании ЗАО «Северо-Западная Нерудная Компания» (Санкт-Петербург). В компании размер оптимального заказа необходимо определять, учитывая, что поставки осуществляются в среднем через каждые два дня. Но есть и специфика. Товар (цемент) привозят по железной дороге. Для того чтобы эти поставки шли с перерывом в два дня, необходимо заказывать цемент у поставщиков с разных железнодорожных направлений. Так как при заказе на одном направлении с перерывом в два дня на одном из перегонов железной дороги решат дождаться других вагонов, адресованных этому же производителю. Задержка в два дня не срок для таких поставок, а ограниченная пропускная способность склада приводит к тому, что одновременно может разгружаться только один вагон, поэтому, если в пути произошло объединение поставок, часть вагонов при выгрузке будет простаивать в очереди. Это повлечет дополнительные издержки по простоям.

Важнейшим пунктом в управлении предприятием является расчет запасов сырья, необходимых для его функционирования. В данной работе на основе математического аппарата представлены наиболее распространенные модели управления запасами и получены выражения расчета оптимального размера заказа.

Современная экономическая наука характеризуется широким использованием математического моделирования. Применение математических методов в единстве с экономическим анализом открывает новые возможности для экономической науки и практики, а также позволяет оценить возможные последствия функционирования предприятия и использовать эти оценки в управлении. Таким образом, овладение математическими методами исследования экономических систем и принятие на их основе оптимальных решений обеспечивает эффективную работу производства.