Модель упругого скольжения в системе «колесо — поверхность дороги»

Введение. С момента появления автомобильного транспорта в машиностроительной области возникла задача обоснования природы сил сцепления системы «колесо — поверхность дороги». Данная проблема была рассмотрена специалистами в области механики, триботехники и математики, которые искали ответ в виде решения контактных задач, позволяющих определить размеры пятна контакта и эпюры касательных нормальных напряжений на площадке контакта [1, 2]. В настоящее время в этой области работает ряд отечественных учёных [3–7]. Одним из основоположников нового направления изучения контактных явлений — механики фрикционного взаимодействия (трибомеханики) — является И. Г. Горячева.

Несмотря на это, до сих пор не существует единого подхода к решению возникшей проблемы. В данной работе сформирована математическая модель, качественно описывающая динамику системы «колесо — поверхность дороги».

Основная часть. Рассмотрим задачу о качении колеса по поверхности дороги. Будем полагать, что жёсткость дороги достаточно велика, в связи с чем её деформациями можно пренебречь. Поверхность колеса зададим совокупностью точек упрого-диссипативно связанными между собой и центром колеса. Положение этих точек в отсутствии деформации колеса будем называть их естественным положением. Координаты естественного положения точек могут быть заданы посредством вектора а * , определяемого углами их отклонения от некоторой фиксированной метки M на колесе. Ограничимся моделью рассматривающей динамику n равноотстоящих друг от друга точек (в своём естественном состоянии) поверхности колеса. Тогда координаты вектора а * будут иметь следующие значения:

а * =[ а * ,а 2 , ™ ,а * ] ^т = П [ 0,2п, - ,2п ( n - 1 ) ] T .                           (1)

Реальное колесо в тангенциальном направлении не является абсолютно жёстким. Колесо деформируется в тангенциальном направлении под действием сил взаимодействия колеса с поверхностью дороги. Отклонение точек колеса от своего естественного положения будем задавать векто-

T ром а = [а1,а2,-,аnJ .

Кроме того, следует учесть тот факт, что в радиальном направлении колесо не является абсолютно жёстким. В результате этого действие вертикальной нагрузки приводит к появлению деформации колеса. Это, в свою очередь, приводит к формированию площадки контакта «колесо — поверхность дороги».

В данной работе не будет рассматриваться динамика этого процесса, а величина радиальных деформаций будет полагаться некоторой фиксированной величиной.

С учётом вышесказанного, моделируемое колесо будет иметь вид, приведённый на рис. 1.

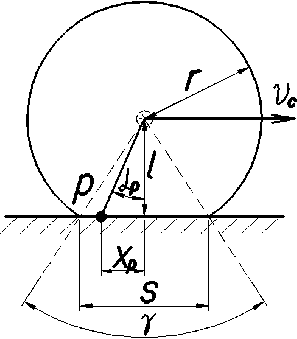
Рис. 1. Контакт «колесо — поверхность дороги»

Здесь r — радиус колеса; s — длина контакта «колесо — поверхность дороги»; l — высота центра колеса; γ — угол контакта; α _p — угол некоторой точки p поверхности колеса;

x _p — расстояние точки p от центра контакта «колесо — поверхность дороги»; v _c — скорость движения центра колеса вдоль горизонтальной оси.

Как видно из рисунка, параметры моде ли запи сываются следующим образом:

l = г ² - т,                                    (2)

Y = arcsin ^— , 2 r

x p = I ^tana p .

Из (4) следует, что линейная скорость точки p относительно центра колеса может быть найдена по формуле:

, = d^x p = I   d ^a p

^pc dt cos² α _p dt ^.

Тогда абсолютная скорость точки p равна:

v p

c cos² a p dt

Сила трения, действующая на точку p со стороны поверхности дороги, может быть найдена по формуле:

F p =- sign ( v p ) f ,                                          (7)

где f — некоторая константа; sign ( • ) — функция знака.

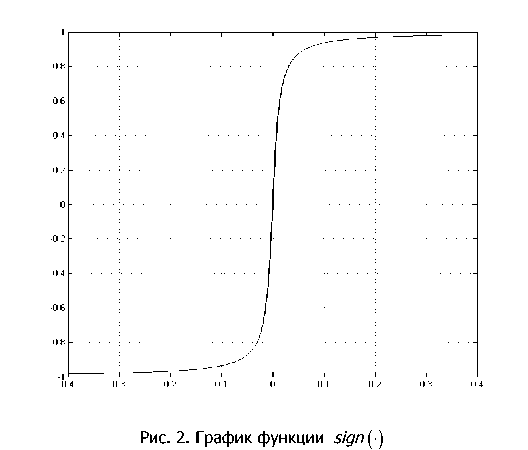
Для реализации мягкой функции знака (рис. 2), в модели использована следующая формула:

sign ( x ) = 2 arctan ( kx ) ,

где k — некоторый коэффициент.

Введём вспомогательные матрицы G и E размера [ n x n ] :												0 0 0 0	0 " 0 0 0
G =	"- 2 1 0 0	1 - 2 1 0	0 1 - 2 1	0 ■ - 0 ■ 1 ■ - 2 ■	0 0 0 0	1 1 0 0 0	; E =	[ 1 0 0 0	0 1 0 0	0 0 1 0	0 ■ 0 ■ 0 ■ 1 ■
	^ 0	0	0	;                  •. 0 ■	- 2	; 1		; 0	0	0	; .. 0 ■	1	; 0
	_ 1	0	0	0 ■	1	- 2 _		_ 0	0	0	0 ■	0	1 _
Тогда матрицы жёсткости		C	и диссипации H			будут иметь вид:

C = c 1 G - c ₂ E , H = h 1 G - h₂E ,

где c1 — коэффициент жёсткости взаимодействия между соседними точками колеса, c2 — коэф- фициент жёсткости взаимодействия точки и центра колеса, h1 — коэффициент диссипации взаимодействия между соседними точками колеса, h2 — коэффициент диссипации взаимодействия точки и центра колеса.

Пусть метка M вращается с постоянной угловой скоростью ω . Тогда динамика точек обода колеса в вариациях относительно их естественного положения может быть задана матричным уравнением:

,d ² a _ d d a        d a )

J —_r = C a + HlF\ a,— ,                           (10)

dt²           dt I , dt )

где F — векторная функция силы, моделирующая сцепление колеса с дорогой, чьи компоненты, с учётом (6)—(8), определяются следующим выражением:

_с и d а ) F l^а , dt н

- f ■ sign

0,

vc

V

- 1

d а i d ф dt dt

cos² ( а i + а * + ф )

J

I a i + а * + ф| <  Y

Iа i+ а /

+ ф| >  Y

где J — момент инерции точек, ф — угол поворота центра колеса; ф = to t .

Динамика центра колеса будет описываться уравнением:

dv с   г- V ( d а ^

m c = F„ + F а, вн / I , dt          /"i l dt J где m — масса колеса, Fвн — некоторая внешняя сила, приложенная к центру колеса (вдоль горизонтальной оси).

Результаты моделирования. Результат компьютерного моделирования показал довольно сложный характер поведения подобной системы. Так, например, диаграмма зависимости угловой частоты некоторой точки колеса от его угла поворота имеет вид, представленный на рис. 3, а. При этом стоит отметить, что имеет место существенная зависимость формы графика от внешней нагрузки и характеристик колеса. Отклонение точки обода колеса от её естественного положения

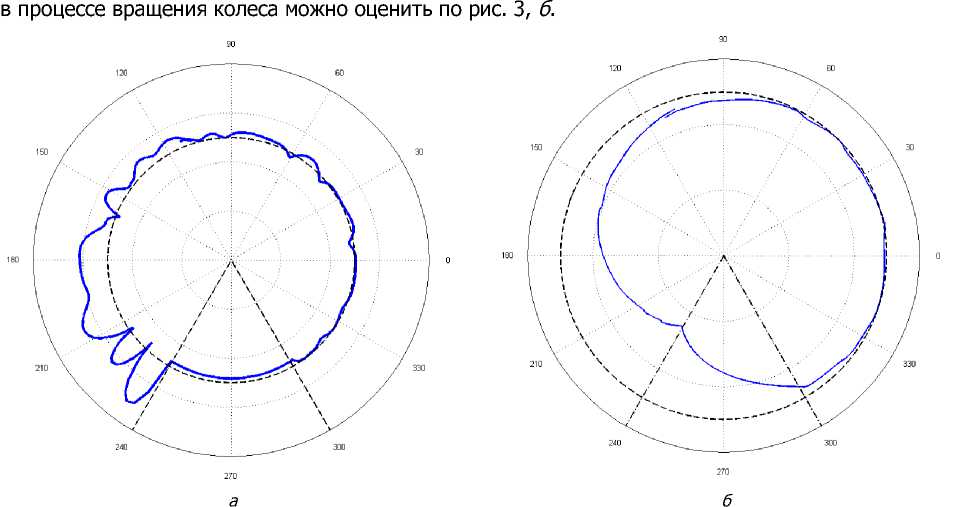
Рис. 3. Угловая частота точки обода колеса ( а ) и её отклонение от естественного положения ( б )

Результат моделирования наглядно подтвердил тот факт, что в случае, когда внешняя нагрузка F_вн препятствует движению, точки колеса, находящиеся в набегающей полуокружности, подвергаются сжатию, а точки с противоположной стороны — растяжению. Это наглядно продемонстрировано на рис. 4, а. В случае сонаправленных векторов скорости движения центра колеса и внешней нагрузки, имеет место обратный эффект (рис. 4, б).

Это явление приводит к появлению эффекта упругого скольжения [5].

По результатам работы математической модели стало видно, что при фиксированной угловой частоте центра колеса в отсутствии классического скольжения (движение точек колеса в зоне контакта), скорость центра колеса в установившемся режиме не является величиной фиксированной и зависит от величины внешней нагрузки Fвн . Для случая на рис. 4, а, скорость точек колеса в зоне зацепления ниже, чем скорость вращения центра колеса. Это приводит к сгущению точек в контакте. Однако, после выхода точки из зоны зацепления, её угловая частота резко возрастает и накопленное натяжение сводится к нулю (рис. 5).

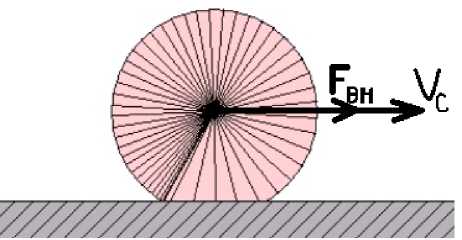
Рис. 4. Моделирование движения колеса при сонаправленной внешней силе и скорости ( а ) и

а                                             б

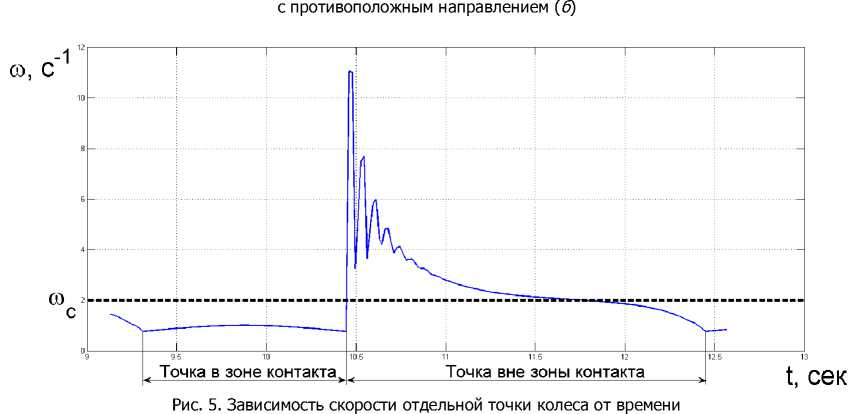
Таким образом, среднее значение от угловой частоты точки обода колеса за период вращения равно угловой частоте вращения центра колеса. Но на поступательную скорость движения колеса оказывает влияние именно скорость точек в области контакта.

Заключение. При качении колеса по поверхности дороги имеет место упругое скольжение. Таким образом, классическая формула связи угловой и линейной скорости ( v_c = R ω) в случае неабсолютно жёсткого колеса, является приближённой. Более точное выражение для линейной скорости должно учитывать F_вн и параметры колеса.

Оценка влияния величины внешней нагрузки на упругое скольжение имеет большое значение для практики, т. к. при наличии упругого скольжения формируется разница расчётного и реального пути, пройденного колесом за некоторый промежуток времени.