Модель усиления частотно-модулированных импульсов в трехуровневых оптических усилителях с изменяющейся нормальной дисперсией с учетом вырождения накачки

диаметра световода, дисперсии, нелинейности.

Принцип действия волоконно-оптического усилителя, как и любого другого квантового усилителя, заключается в создании в активной среде под действием волны накачки инверсии населенности и воздействии на среду слабого резонансного электромагнитного поля, которое приводит к индуцированным переходам с верхнего метастабильного уровня в основное энергетическое состояние и в результате этого - к усилению данного поля. В настоящей работе рассматриваются волоконные оптические усилители, работающие по трехуровневой энергетической схеме. К этому типу волоконно-оптических устройств можно отнести (с известными допущениями) наиболее часто встречающиеся эрбиевые и иттербиевые усилители, а также усилители, работающие на основе ВКР. В работе получены условия существования ЧМ симиляритонного волнового пакета в неоднородном по длине трехуровневом усилителе и анализируется динамика его устойчивого распространения.

Рассмотрим более подробно эрбиевый волоконный усилитель, работающий по трехуровневой схеме. Расположение энергетических уровней иона эрбия позволяет реализовать рабочие переходы электрона с возбужденных уровней 4 I9/2 и 4 I11/2 вначале в метастабильное состояние 4 I13/ 2 , а затем – с метастабильного в основное состояние 4 I15/2 . Последний переход соответствует интервалу длин волн 1.53…1.6 мкм. Инверсная населенность в такой трехуровневой среде достигается за счет большого времени жизни на метастабильном уровне (порядка 10 мс). При этом время релаксации с уровней, соответствующих уровням накачки, на метастабильный уровень составляет несколько микросекунд. Для со- здания инверсной населенности используется излучение с длиной волны, попадающей в одну из полос поглощения в соответствии с указанной схемой энергетических уровней. Отметим, что за счет значительного штарковского расщепления в кварцевом стекле появляется возможность накачки непосредственно в полосу, соответствующую метастабильному уровню. При использовании накачки на длине волны 0.98 мкм усилитель работает по трехуровневой схеме, а при использовании накачки на длине волны 1.48 мкм – по квазитрехуровневой. Наиболее высокая эффективность накачки достигается на длине волны 1.48 мкм, при которой волоконный усилитель работает по квазитрехуровневой схеме.

Усиление в рассматриваемой схеме энергетических уровней может быть описано системой уравнений: [5]

dN 2 dt = K p ( N - N ,) - K s [(1 + b)N ₂ - bN - N ₂ 1 x 21 , 2 y =^ ^T s [(1 + b ) N ₂ - bN ].                         • ⁽¹⁾

Здесь использованы следующие обозначения: N ₂ и N — населенность метастабильного уровня и общая концентрация ионов эрбия; Х ₂₁ - время жизни на метастабильном уровне; T p - сечение поглощения накачки, T s - сечение эмиссии на длине волны усиливаемого сигнала, b – отношение сечения поглощения к сечению эмиссии на частоте v s ; параметр у (z ) имеет смысл локального инкремента усиления, параметры P p и P , - доли мощности накачки и усиливаемого сигнала; K_p и K_s – скорости накачки и излучения. В стационарном состоянии населенность мета-стабильного уровня можно считать постоянной во времени, т.е. dN ₂ / dt = 0 , в результате чего получаем:

N ₂ = N ( K p + bK s )/ [ K p + (1 + b ) K s + 1/ x ₂₁ ] . (2)

Подставляя это выражение во второе уравнение (1) системы, находим выражение для инкремента усиления:

1 ^T s b s ^{N (} K p ^{- b} / ^x 21 )

2 K p + (1 + b ) K s + 1/ x ₂₁ .      ⁽³⁾

Запишем теперь уравнения, определяющие трансформацию вдоль световода интенсивностей волны накачки I_p , усиленной сигнальной волны I_s и волны спонтанной люминесценции в случае попутной накачки:

dIp /dz = -IpTp(N-N2) , dIs / dz = 2yIs , dIf Idz = [(1+b)N2 -bN]hvsAv+2yIf ,

где hvs и Av - энергия фотона и ширина линии излучения для усиленной спонтанной люминесценции. При решении уравнений (4) необходимо учесть, что для скоростей накачки Kp и излучения Ks справедливы соотношения [6]:

K p ⁽ z ) = ^T p b p I p ⁽ z V ^{h v} p ,

K s ( z ) = TP s [ I s ( z ) + I f ( z )]/ h v , .    ⁽⁵⁾

В нашем случае, считаем, что источник (например, эрбиевый волоконный лазер) обеспечивает генерацию пикосекундных импульсов с частотой следования v_скв . В этом случае средняя интенсивность последовательности стоксовых сигналов может быть оценена как I s ( z ) = V _CKBW_S ( z ) , где W , ( z ) - энергия отдельного стоксова импульса на длине световода-усилителя z .

Полагая концентрацию ионов по длине световода постоянной, можно показать, что суммарная скорость вынужденных переходов не меняется вдоль световода, что аналогично сохранению числа фотонов при рамановском рассеянии [7]:

K p ( z ) + (1 + b ) K , ( z ) = K о .       (6)

Для общей интенсивности излучения Iz = Is + If на частоте vs получаем dIz / dz = 2/(I + hvsAv /^sGs).   (7)

Вследствие малости ширины линии спонтанной люминесценции A v , вторым слагаемым в правой части (7) можно пренебречь. После этого выразим коэффициент усиления У и подставим в (4), в результате чего получаем для интенсивностей накачки и излучения следующую систему уравнений:

dK / dz = дД К - % К

• 2           R R р 2    s*s 2

^dIp I ^dz = ^{- ( v} p I P p V , ) g R I p I 2 - % p I p ,

„   NPHTTp      Nbnas       Ntp gR =---------------, %, =, %p =--------.

• ^{( K} 0 ^{+ 1/ X} 21 ) ^{h v} p        ^K 0 ^X 21 ^{+ 1         K} 0 ^X 21 ^{+ 1}

Приведенные уравнения, описывающие эволюцию сигнала и накачки, аналогичны системе, описывающей рамановское рассеяние и оказываются универсальными для усилителей, работающих по трехуровневой схеме.

Главным отличием ВКР-преобразования от преобразования на вынужденных переходах является его меньшая эффективность. Коэффициент преобразования g_R для эрбиевого усилителя в 10²-10³ выше, чем в рамановском усилителе. Однако коэффициент ВКР-преобразования g_R обладает гораздо более широким спектром. В случае эрбиевого усилителя частотная зависимость коэффициента g_R ограничивается резонансной полосой поглощения накачки.

Возвращаясь, к уравнениям (8), следует от- метить, что соотношение между первыми слагаемыми в правой части, описывающими преобразование накачки, и вторыми, характеризующими поглощение накачки и сигнала, определяется отношением скоростей вынужденных и спонтанных переходов: KpT21 - в уравнении для роста интенсивности сигнала и KT21 / Пр — в уравнении для интенсивности накачки. Время жизни на метастабильном уровне для распространенных сортов стекла T21 ~ 10 мс. Типичные для эрбиевого усилителя мощности сигнала 0,01 Вт и накачки 10 Вт соответствуют скоростям переходов 105–108 в секунду. Отсюда следует, что основное изменение интенсивности сигнала вызвано истощением накачки. При этом поглощением накачки и сигнала в волокне, описываемым вторыми слагаемыми уравнений (8), можно пренебречь.

В данном приближении система уравнений (8) легко интегрируется. Сохранение числа фотонов в системе записывается как

I + (v /л v)L = L = I „ + (v /nv)(9) p V p • p s/ 2 0 p0 p p Ip 20, здесь Ip0 - начальная интенсивность накачки (на входе в усилитель), 120 — суммарная интенсивность сигнала и спонтанной люминесценции на входе в усилитель. В этом приближении интенсивностью спонтанной люминесценции можно пренебречь по сравнению с интенсивностью сигнала, и поэтому далее мы полагаем 120 ~ Is 0 и 12 = Is.

В результате интегрирования уравнений (8) приходим к следующему выражению для эффективного инкремента усиления сигнальной волны нала достигает своего предельного значения Is0(1 + Д0) . На рис. 1 приведены зависимости относительной интенсивности сигнала I /1 „ от s     s 0

длины усилителя z, полученные для отношения интенсивностей накачки и входного сигнала Ipо / Is о = 10, 100, 1000 (кривые 1-3) и значениях параметров: N = 5-1024 м~3, Л = Л = 0-9 , ps v = 1530 нм, vD = 1480 нм,   о = 3 • 10 25 м2, s        ^-25 2 p                     p о = 2 • 10 м , которые будут нами использованы и далее. Видно, что по мере распространения сигнала по световоду происходит насыщение интенсивности сигнальной волны при значениях z 0 ln Д0 / P. С ростом накачки максимальная интенсивность сигнала возрастает.

Особенностью самоподобного симиляритон-ного распространения импульса является то, что его огибающая, независимо от своей начальной формы, асимптотически стремится к параболической форме, масштабирующейся с ростом координаты импульса [1-3]. При этом общий вид импульса может быть представлен в виде

A ( t , z ) = A ( z )Y ar_r ( z , r )exp[ z ( 0 ( z ) + a ( z 'p² )] ,(12)

где P = t —

£ dz' / u ( z ')

– время в бегущей систе-

ме координат, u ( z ) = ( д Д ( z)/ 9 ^ ) 01 - групповая скорость, Д ( z ) - константа распространения, ^ ( Z ) - фаза импульса, 6 Z ( z ) - скорость ЧМ (которая для симиляритона является постоянной величиной). Функция Y p _ar ( p , z ) задает форму огибающей, которая для импульса параболической формы и длительностью T s ( z ) определяет-

G, ( z ) = ef

I s ( z )

I s 0

(1 + A ,)exp ^ z Д ₀ + exp P z

ся выражением

где введены параметры Д = ^ p V s I p 0 / v _pI_s 0 и

N n До о   I

Q T                         * s’ ^{0 s} p            0

^P = I 0 g R =-- no (1 + b ) + До I ' s s ^x '      ' 0 p p 0

•

Если начальная интенсивность накачки на-

много превосходит начальную интенсивность сигнала ( I_{s 0} >>  I p ₀ = I ₀ ), то P = N n s o s и (10) можно переписать в виде

Д exp P z

G f ( z ) =       ----

Д ₀ + exp P z

При малых z , когда справедливо P z 0 ln( I ₀ / I s ₀) , наблюдается экспоненциальный рост эффективного инкремента усиления сигнальной волны, т.е. ^G ef ⁽ z ) = ^exp^{( P z} ) .

Постепенное истощение накачки приводит к тому, что начальный экспоненциальный рост энергии импульса замедляется, коэффициент усиления стремится к нулю и интенсивность сиг-

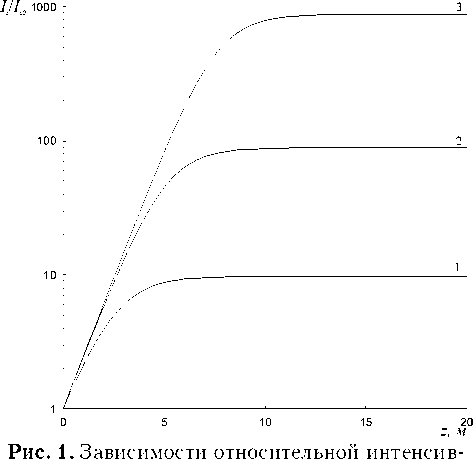
ности сигнала от длины усилителя, при отношении интенсивностей накачки и входного сигнала I p 0 / I s 0 = 10, 100, 1000 (кривые 1-3)

V¹ - ^{т 2} / ^t S ⁽ z ), ^т ^ т ⁽ z )>

⁰ ,                ^т >  т (z ) ,   ⁽¹³⁾

Т ^{( z} ) = ^т 0

1 +

6 « 0 D 0 А

(1 + р0 ) lnl 1 +

exp A z — 1 1 + р 0

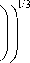
. (18)

Известно, что условие образования устойчивого симиляритона, при котором для нелинейного уравнения Шредингера имеется точное решение в виде ЧМ импульса параболической формы, может быть представлено в виде:

g f ^{- 3} ^ 0 ^D 0 = ⁰ ,            (14)

где параметры D ₀ и 6Z0 - входные значения ДГС и скорости ЧМ. Эффективный инкремент усиления неоднородного световода связан не только с его материальным коэффициентом усиления у (z ) , но и с площадью моды 5 * ( z ) , ДГС d ( z ) = ( д ² р / а « ²) ₀ и керровской нелинейностью R ( z ) соотношением [8]

На рис. 2 представлены зависимости относительной длительности усиливаемого импульса Т s / T q от длины световода, полученные для указанных выше (см. рис. 1) параметров. Видно, что по мере увеличения длины усилителя наблюдается рост длительности импульса. С увеличением интенсивности накачки длительность сигнала также увеличивается. При достаточно больших длинах усилителя эта зависимость имеет следующую асимптотику:

g f ⁽ z ) = У ⁽ z ) ^-

д S„ / д z д D / д z д R / д z 1

2 S m      2 D 2 R

т s ( z ) □ T q ( 6 « q D о ( 1 + Р о ) z ) 1^/3 . ⁽¹⁹⁾

Профиль ДГС усилителя, обеспечивающий самоподобный режим распространения ЧМ импульса параболического типа, получаем, подставив в (18) выражение (10) для относительного усиления G_ef ( z ) :

В случае однородного активного световода условие (14) может быть записано в предельно простом виде у 0 — 3 ^ 0 D 0 = 0 .

Далее мы будем рассматривать так называемые световоды с W- профилем радиального распределения показателя преломления [9, 10]. Для указанных световодов нелинейность и площадь моды слабо зависят от внешнего диаметра, поэтому для них эффективный инкремент усиления (15) определяется материальным усилением и профилем дисперсии. Профиль ДГС, обеспечивающий самоподобную эволюцию ЧМ импульса с постоянной скоростью ЧМ может быть выражен через эффективный инкремент G_ef ( z ) как [14]:

D ( ^z )                      ^{(1+ р} о )ехр й г

=                                                                     .

D |     б ^ Д,      . | I R (exp A z — 1) ||,

⁰      1 +       ( 1 + R ) ln 1 +        ------ ( exp ti z + R ) (20)

I A ⁰⁷ (      I q q (1 + R q ) JJ^{V          07}

При I_s 0 / I_p 0 □ 1 и малых z профиль ДГС волоконного трехуровневого усилителя, обеспечивающего распространение самоподобных параболических импульсов, не должен зависеть от отношения интенсивностей сигнала и накачки:

D ( z ) D 0

И V 1

□ 1 + А — б ^ D — l z . v

V                   р 7

D ( z ) =

D0Gef(z)

1 + 6«0Do\G.(z')dz' •

С учетом этого соотношения можно записать выражение для длительности симиляритонного импульса в неоднородном усилителе

^T s ^{( z} ) = ^т 0

1/3

. (17)

Если световод считать пассивным, т.е. принять у = 0 , то для длительности импульса получаем известное соотношение Т ⁽ z ) = ^т 0 ( 1 ⁺ 6 « 0 ^D 0 z ) ^1/3 .

Рассмотрим теперь характеристики симиля-ритонного импульса, распространяющего в волоконном усилителе, работающем по трехуровневой схеме. Подставив в соотношение (17) выражение для относительного увеличения энергии импульса (10), получаем для длительности сигнала в подобном усилителе:

На рис. 3 представлены профили ДГС эрбиевого усилителя, обеспечивающие симиляритон-

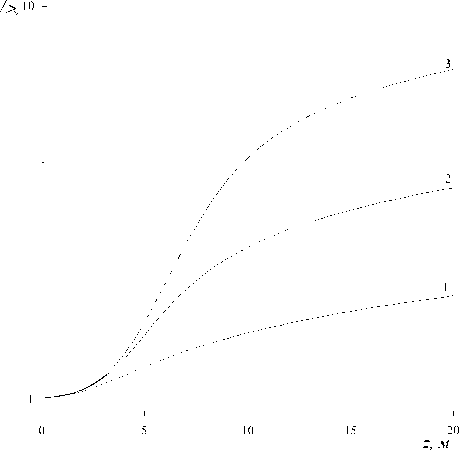
Рис. 2. Зависимости относительной длительности сигнального импульса от длины усилителя:: 10, 100, 1000 (кривые 1-3)

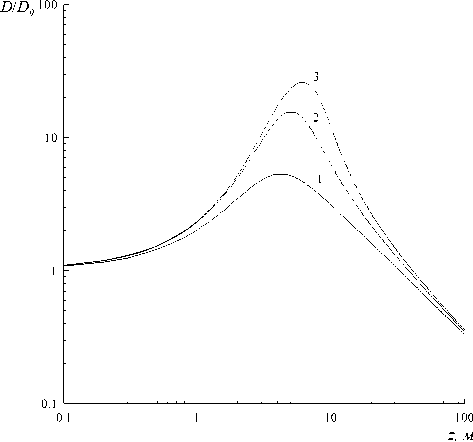
Рис. 3. Профили ДГС, полученные при 10, 100, 1000 (кривые 1-3)

ный режим распространения импульсов, полученные при а ₀ = 10 24 с ², D 0 = 5 ■Ю ²⁷ с 2 / м . Видно, что быстрый и близкий к экспоненциальному рост ДГС по мере истощения накачки должен сменяться гиперболически убывающим профилем, обеспечивающим самоподобное распространение усиленного сигнала.

Практический интерес, в основном, представляет участок со значительным усилением, на котором реализуется рост ДГС и происходит существенное поглощение накачки. В связи с этим найдем оптимальную длину рассматриваемого усилителя, при которой происходит максимальное повышение уровня входного сигнала. Отметим, что до сих пор расчет велся без учета поглощения накачки и сигнала, поэтому максимальный предельный уровень сигнала не достигался на конечной длине усилителя. Влияние слабого поглощения можно оценить, положив в системе (8) коэффициенты поглощения накачки и сигнала равными (%p = %s = %) [11]. В этом случае величина I0 , введенная соотношением (9) и ответственная за число закачанных и возбужденных фотонов в усилителе, уже не постоянна по его длине. В этом случае зависимость их числа от пройденного пути z определяется уравнением d L , Vp

I p ⁺       I s = ~TI 0 = - % I 0 - (22)

dz ^     ^pvs   J dz

Решая его, для интенсивностей сигнала и накачки имеем

I , ( z ) =

( P 0 + 1)e ^x P S z I

P0 + exp Sz exp( - %z),

I ( z ) = ^p

P 0 + 1 I

Д ₀ + exp S z ^{p 0}

exp( - % z )

Из условия максимума интенсивности сигнала I_s ( z ) на выходе из усилителя получаем выражение для его оптимальной длины

L o _pt = S -'ln ( ( S / % - 1) P _o ) . (24)

При длинах S z >>  1 и % z « 1 спад интенсивности сигнальной волны происходит по линейному закону I s ( z ) = I s 0 ( Д , + 1)(1 - % z ) .

На рис. 4 представлены зависимости интенсивности сигнала (с коэффициентом, зависящим от эффективности накачки) ( v _p l^p v s ) I s и накачки I_p от длины усилителя, полученные с учетом поглощения в волоконном световоде усилителя % = 5 ■Ю^{- 3} м ^{- 1} при отношении начальных интенсивностей I_{p 0} l I s ₀ = 1000. Пунктиром показана зависимость I 0 ( z ) . Видно, что при достижении длины световода величины L_opt интенсивность волны накачки спадает практически до нуля, а интенсивность сигнальной волны достигает максимального значения. Дальнейшее увеличение длины усилителя приводит к медленному и практически линейному спаданию выходной интенсивности сигнальной волны.

Таким образом, в результате проведенного в работе анализа получены условия возникновения устойчивых ЧМ импульсов параболической формы в неоднородных усиливающих световодах в области нормальной ДГС. Получено выражение для профиля ДГС, обеспечивающего оптимально быстрое усиление импульсов и показана эффективность использования в качестве усилителей световодов с увеличивающейся дисперсией и относительно большим инкрементом усиления. Получены соотношения, позволяющие

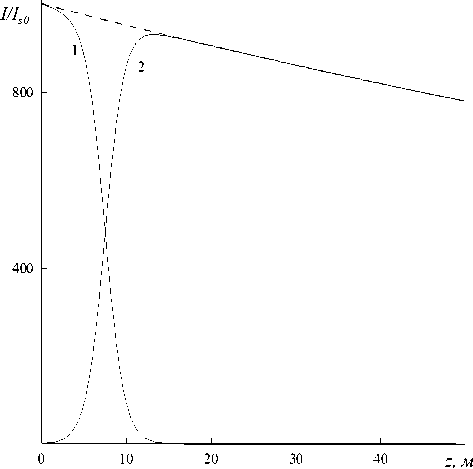
Рис. 4. Зависимости интенсивности накачки и сигнала (кривые 1, 2) от длины усилителя при учете поглощения; 1000

изготовить эрбиевый волоконный усилитель с профилем ДГС, обеспечивающим самоподобный режим усиления ЧМ импульсов, и подобрать необходимый уровень накачки для заданных профиля ДГС и уровня сигнала, а также подобрать оптимальную длину усилителя.

Кроме того, заметим, что полученный на выходе из неоднородного световода ЧМ импульс можно дополнительно сжать, если осуществить компрессию чирпованного импульса в среде с аномальной эффективной дисперсией. Это можно осуществить, например, на паре дифракционных решеток, или в фотонно-кристаллическом световоде с малой керровской нелинейностью [7]. В последнем случае систему можно сделать полностью волоконной.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральных целевых программ «Научные и научно-педагогические кадры инновационной России на 2009 - 2013 годы» и «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы»