Модель возбужденного состояния и линия стеклования жидкости

Введение. В модели возбужденного состояния [1,2] предполагается существование в жидкостях и аморфных средах кинетических единиц, смещенных или способных сместиться на критическое расстояние Дг_т, соответствующее максимуму силы межатомного притяжения (рис. 1). Такое предельное флуктуационное смещение -возбуждение кинетической единицы - обусловлено перегруппировкой соседних частиц и служит элементарным актом процессов вязкого течения, стеклования жидкостей *и пластической деформации стекол. Такую кинетическую единицу (атом, группу атомов) будем называть «возбужденным атомом».

В настоящей работе с точки зрения данной модели рассмотрена зависимость температуры стеклования от давления, называемая линией стеклования. Полученные результаты сравниваются с термодинамической теорией стеклования [3].

Модель возбужденного состояния и линия стеклования. Вероятность критического смещения атома W=N_e7N в жидкостях и аморфных средах выражается соотношением [1,2]

• ¹    Работа выполнена при финансовой поддержке «Лучшая научная школа».

  N

  —- = exp N

  
  

ЯГ2Агм<Рт + Р) кТ

( Ув_£ + PA V )

exp----------- .           (1)

Ч кТ )

Здесь отношение NJN" равно концентрации (доле) возбужденных атомов. Элементарный объем kv_t = яг² &г_И представляет

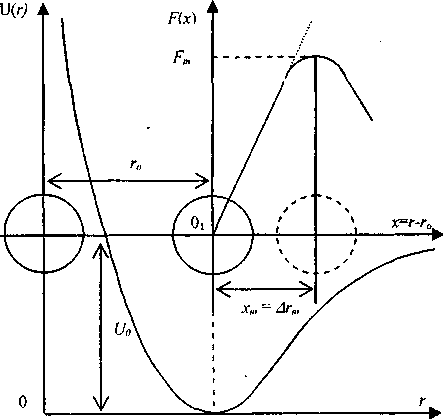
Рис. I. Схема возбуждения атома. г_о - среднее межатомное расстояние. Дг_л, - критическое смещение атома, соответствующее максимуму силы межатомного притяжения.

РФФИ (код проекта 05-01-00071а) и гранта БГУ собой флуктуационный объем, необходимый для процесса возбуждения атома (яг2 - площадь сечения атома). Иными словами, характеризует минимальную флуктуацию объема системы, необходимую для критического смещения атома. Энергия процесса возбуждения атома AEe=PmAvc равна работе против максимального внутреннего давления Рт, обусловленного силами межатомного (межмолекулярного) притяжения. Она представляет собой приращение внутренней энергии системы в процессе возбуждения атома.

Одним из важных параметров модели является флуктуационный объем системы =N_tAv_e,               (2)

его объемная доля тесно связана с концентрацией возбужденных атомов г Л f

• ⁷ V v\М)

,       ( Ae^PAvA

/= — ехР — Ь (3> где v=V/N - атомный объем. При охлаждении стеклообразующей жидкости до температуры стеклования T=Tg величина / уменьшается до некоторого минимального значения >^[U]

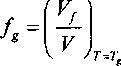
ниже которого (при Tg) замораживаются процессы рождения и исчезновения возбужденных кинетических единиц. Оценку f_g можно получить по данным о значениях вязкости вблизи Tg.

Полагая независимость параметров Д^, dve и fg от температуры Tg и давления Pg стеклования, из основного уравнения (3) для линии стеклования получаем следующее выражение dPg = *1п(Ду,/./,у)

dTs

Введем энтальпию процесса возбуждения атома AH_es которая в отличие от zl^ равна работе, совершаемой не только против внутреннего давления, но и против внешнего давления Р [4,5]

АН, = (^, + ^)Ave = Д^ + PAv,.

Разрешив уравнение (3) относительно (Э^+РЛуД с учетом (6) при T=T_g имеем

AHc=kTAx(AvJ/sv).(7)

Принимая во внимание это соотношение, линию стеклования (5) можно представить окончательно в виде

А^_ dTs TAV« что по внешнему виду аналогично известному уравнению Клапейрона-Клаузиуса для равновесных фазовых переходов [4]

dP Ад

"dT~ TAV где Т и Ад - температура и скрытая теплота фазового перехода, соответственно Ziv -изменение объема при данном переходе. Отношение Aq/Т равно энтропии фазового перехода А8ф=Ад!Т.

По аналогии с этим выражением на основе равенства (8) введем величину с раз- мерностью энтропии физический смысл которой обсуждается ниже. Условно ее можно назвать «энтропией квазифазового перехода жидкость-стекло» или «энтропией процесса возбуждения атома».

Линия стеклования в неравновесной термодинамике. Один из важных результатов описания процесса стеклования в рамках неравновесной термодинамики состоит в том, что линия стеклования в отличие от таковой для равновесных фазовых переходов определяется свойствами только одной жидкой фазы. Зависимость давления стеклования P_g от T_g выражается уравнением [3]

dP_g AQ dT_g ' T_gAV’

(Ю)

где AQ - теплота процесса неравновесного структурного превращения, AV - изменение объема при данном превращении. Величины AQ и AV определены производными свободной энергии Гиббса по внутреннему параметру £ который наряду с парой внешних параметров (Р, 7) выступает как равноправный. Стеклообразное состояние соответствует частному случаю, когда £= const. Точка стеклования для заданного £ определяется как точка

Из соотношений (8) и (10) следует связь между параметрами термодинамической теории и модели возбужденного состояния

АС^Л^

ДИ Ave ’

113 ся произведением параметров потенциала Ми ((/ = -АЕ^+ВЕ") [6]: dve/v «9/тп^ где тп является функцией коэффициента Пуассона в [7], с учетом которой данное отношение объемов, в свою очередь, оказывается однозначной функцией ц где все величины отнесены к молю вещества. С этих позиций критическое смещение (возбуждение) атома, или предельная деформация межатомной связи (рис. 1), есть неравновесное структурное превращение.

Модель возбужденного состояния можно рассматривать как один из вариантов термодинамической теории [3], где в качестве внутреннего параметра выступает доля флуктуационного объема ^~f{T,P\ которая при Tg постоянна f=f_s~ const в соответствии с критерием в неравновесной термодинамике £= const.

Степень неравновеености стекла. В термодинамической теории стеклования [3] (см. формулы (11) и (15) в работе [3]) отношение AQiT_& в равенстве (10)

AS = ^

Таким образом, для оценки Р₈ окончательно получаем следующее выражение

3(1-2//)

2Л(1+^)

имеет смысл отклонения энтропии неравновесного состояния (стекла) от ее равновесного значения в точке стеклования (7_g, P_g), в которой состояния жидкости и стекла неразличимы [3]. Следовательно, Z1S можно рассматривать как меру неравновеености стекла вблизи T_g.

Естественно предположить, что такой же сцысл имеет величина dS,, в аналогичном выражении (9), следующем из модели возбужденного состояния. Поэтому, разделив обе части равенства (9) на постоянную Больцмана к, введем безразмерную «энтропию квазифазового перехода жидкость-стекло»

Значения коэффициента Пуассона (при Tg) брали из справочников [8,9] и других источников [10,11], а долю флуктуационного объема Д вычисляли из данных о вязкости вблизи T_g по соотношениям [12]

1           Т -Т

Л ~ _С| ’ Л - _в > где С_ьВ и Т_о - постоянные уравнений Вильямса-Ланделла-Ферри [13] и Фогеля-Фульчера-Таммана [12] соответственно. Известно, что эти уравнения вполне удовлетворительно описывают температурную зависимость вязкости в области стеклова

ния. Результаты расчетов приведены в табл. 1-5. В них также приводятся парамет

ры модели ДН_е и dv_e, рассчитанные соответственно по соотношению (7) и формуле [14]

Дгг =

3(1-2//)^

^_ЛЯ.

8 к кТ. ’

которую назовем «степенью неравновесно-сти стекла».

Эту величину можно оценить по формуле (см. (7) и (12))

^^1п

Отношение объемов (Zh^ /v) определяет-

где Е - модуль упругости при одноосной деформации.

Обсуждение результатов. Постоянство pg в области стеклования. Прежде всего, при заметных изменениях доли флуктуационного объема (4*0.010-0.030) и коэффициента Пуассона (д *0.20-0.33) обращает внимание достаточно устойчивое приближенное постоянство степени неравновесно-сти (15) вблизи 7g для стекол различной химической природы (табл. 1-5)

p=^h*const*3. (17)

kTg

Следовательно, жидкость переходит в стекло, когда средняя энергия теплового движения kTg становится в первом прибли-

жении в 3 раза меньше энтальпии возбуждения атома ДН_е.

У калиевоборатных стекол, например, при росте содержания окиси КзО от 0 до 33.5 мол.% множитель (dv/v) в равенстве (13) убывает со значения 0.56 до величины 0.45 (д растет с 0.262 до 0.303), а множитель 1(4 увеличивается от 29 до 38 и в результате этого логарифм произведения (zhVv)(Vf_g) в соотношении (13) оказывается практически постоянным р_к^ const ^2.8 (табл.2). Как правило, стекла с низкой долей флуктуационного объема f_g имеют высокое значение коэффициента Пуассона (табл. 1-5). В частности, сульфатнофосфат-ные стекла (табл. 4) характеризуются низкими значениями,4^0.013-0.20 и высокими величинами //»0.280-0.300. У щелочноси-ликатных стекол (табл. 1), наоборот, значения д сравнительно малы (-0.22-0.25), a f_g выше (-0.028-0.030), что и приводит к постоянству Р_й для разных стекол.

Одна из причин лучшего выполнения постоянства Pg в сравнении с f_g« const (табл. 1-5), по-видимому, заключается в компенсации множителем (dv/v) зависимости f_g от ангармонизма колебаний квазирешетки стекол. Поскольку образование возбужденного атома связано со значительным отклонением кинетической единицы из равновесного положения и с проявлением нелинейности силы межатомного взаимодействия (рис. 1), доля флуктуационного объема f_g оказывается функцией решеточного параметра Грюнайзена yt -меры ангармонизма [15], В свою очередь, величина ус является функцией коэффициента Пуассона [16]

Следовательно, отношение объемов dv/v, согласно (14), обратно пропорционально уь Например, при росте ангармонизма y_L с увеличением содержания окиси калия в калиевоборатных стеклах величина 1(4 растет, a (dv/v) уменьшается (табл.2). В результате такой взаимной компенсации друг друга указанными множителями произведение (Av_e/v)(Uf_g) остается постоянным.

Тем не менее следует признать, что степень неравновесности стекол (%, хотя и слабо, но зависит от природы стеклующихся веществ. Постоянство Pg выполняется лучше для стекол одного структурного типа. При переходе от одних из них к другим величина Pg меняется. Так, для щелочноси-ликатных стекол имеем Pg~3 (табл.1), для сульфатнофосфатных - /5^3.4 (табл .4), для калиевоборатных - /4^2.8 (табл.2). У органических аморфных полимеров степень неравновесности заметно ниже (pg«2.5, табл.5), чем у неорганических стекол (fg-3, табл. 1-4). И внутри групп стекол одного типа наблюдаются изменения /(,. Так, например, в халькогенидных стеклах As-S при изменении содержания As степень неравновесности меняется вполне определенным образом. При возрастании содержания мышьяка с 10 до 40 ат.% pg падает с 3.3 до 2.8 (табл.З). Известно, что стеклообразная сера имеет преимущественно линейную цепочечную структуру. Введение мышьяка приводит к сшиванию цепей. При этом происходит переход от линейной (AS10S90) к трехмерноувязанной сетчатой структуре (As4OS6o). Такой переход сопровождается уменьшением ангармонизма: решеточный параметр Грюнайзена у^ рассчитанный по формуле (18), снижается с д=3.8 доу/-2.! (табл.З).

Структурные изменения в процессе возбуждения атома. Из классической термодинамической теории флуктуации плотности и модели возбужденного состояния следует, что доля флуктуационного объема является функцией относительной флуктуации плотности [14,15]

. (19) Р /

Следовательно, процесс возбуждения атома тесно связан с флуктуацией плотности t^Av_e/v«consp. В отсутствие последней tfAp/pf=Vpy флуктуационный объем аморфной среды равен нулю/=0.

В термодинамической теории флуктуации обычно рассматриваются изменения плотности, обусловленные общим (равновесным) увеличением или уменьшением расстояний между частицами, несколько искажающими однородность жидкости в малых объемах, не нарушая ее существенным образом. Однако, как показывают, в частности, численные эксперименты [17], на самом деле во всякой макроскопически однородной аморфной среде наряду с такими «гомофазными» флуктуациями существуют «гетерофазные» флуктуации плотности [18], приводящие к образованию зародышей новой фазы, например, твердой фазы в локальных областях однородной жидкости,

Таблица 1. Коэффициент Пуассона //, доля флуктуационного объема ^ и степень неравно весности ^ для кварцевого стекла SiO2 и щелочносиликатных стекол R:O-SiO2 (R=Li, Na, К)

Стекло	К	Л		Мс У	Jve, Е3	ДНИ кДж /мол ь	9»
SiO: R2O-SA LiA МОЛ.%	1423	0.03	0.170	0.85	17	39	3.3
28.6	688	0.028	0.205	0.73	8	19	3.3
30.0	686	0.027	0.208	0.72	8	19	3.3
32.6	684	0.029	0.213	0.71	7	18	3.2
35.9	680	0.029	0.20	0.75	7	18	3.2
41.3 NaA мол.%	675	0.029	0.231	0.66	6	17	3.1
19.6	744	0.029	0.234	0.65	10	19	3.1
29.45	715	0.028	0.254	0.59	9	18	3.1
30.1	713	0.028	0.255	0.59	9	18	зл
32.9	704	0.028	0.255	0.59	9	18	3.1
ЗбТ К2О,	694	0.029	0.255	0.59	8	18	3.1
мол.% 16.7	766	0.030	0.236	0.64	11	20	3.1
18.8	760	0.029	0.244	0.62	11	20	3.1
21.4	745	0.029	0.254	0.59	11	19	3.0
26.9	733	0.028	0.275	0.53	11	18	29
28.7	728	0.028	0.281	0.51	И	17	2.9
. 33	715	0.027	0295	0.47	И	17	2.9

Критическое смещение (возбуждение) атома, соответствующее фактически разрыву межатомной связи (рис.1), можно рассматривать в качестве примера подобных гетерофазных флуктуаций. Жидкость испытывает местные «разрывы», не приво-

115 дящие, однако, к существенным макроскопическим изменениям структуры, поскольку каждый атом жидкости, теряя связь с одним из соседей, сохраняет связи со всеми остальными соседними частицами [18].

Таблица 2. Параметры модели возбужденного состояния для калиевоборатных стекол К2О-В2Оз

К2О, мол. %	Т„ К		Л	Ziv,, Г?	V	П	АН,, кДж МОЛЬ	А
0	578	0.262	0.034	20	0.5 6	1.8	13	2.8
1.1	582	0.292	0.034	16	0.4 8	2.2	13	2.6
2.5	588	0.293	0.033	15	0.4 8	2.2	13	2.7
3.9	597	0.293	0.032	14	0.4 8	2.2	13	2.7
85	623	0.293	0.030	13	0.4 8	2.2	14	2.8
13.0	658	0.295	0.030	13	0.4 7	2.2	15	2.8
18.0	685	0.301	0.029	13	0.4 6	2.3	16	2.8
22.8	7Н	0.295	0.028	13	0.4 7	2.2	16	2.8
28.2	723	0.288	0.027	12	0.4 9	2.1	17	2.9
33.5	706	0.303	0.026	II	0.4 5	2.3	17	2.9

В формуле (19) левая часть равенства / относится к отдельным возбужденным атомам и обусловлена гетерофазными флуктуациями плотности («неравновесным структурным превращением»), а правая часть представляет собой результат обычных (равновесных) гомофазных флуктуаций плотности и относится ко всем атомам образца. Такая несогласованность оказывается лишь кажущимся противоречием, поскольку с точки зрения классической термодинамики, имеющей дело со средними значениями величин за очень большие (фактически бесконечно большие) промежутки времени, различие между гетерофазными и гомофазными флуктуациями плотности не имеет принципиального значения [18].

Более того, результаты расчета флуктуационного объема, следующие из модели возбужденного состояния, можно получить и в том случае, если отказаться от представления о гетерофазных флуктуациях, и в соответствии с равновесной термодинамикой флуктуационный объем (2) считать распределенным равномерно между всеми частицами жидкости [17]

^^^Д^ =Л^(Дг)\ (20) где 7V - общее число частиц, Avz = (Дг/ -средний флуктуационный объем, приходящийся на одну частицу, Дг - среднее смещение атома из равновесного положения.

С помощью метода молекулярной динамики было показано [17], что в области стеклования для простых жидкостей, межатомное взаимодействие которых описывается потенциалом Леннарда-Джонса, флуктуационный объем (20), определенный по средним смещениям атомов, совпадает с величиной V^ полученной по модели возбужденного состояния (2), т.е. имеет место равенство: Л(,Дт_Е = NAv_z. Данный факт объясняется указанным выше свойством равновесной термодинамики, согласно которой нет разницы между гомофазными и гетерофазными флуктуациями плотности: образование флуктуационного объема в результате (неравновесных) критических смещений возбужденных атомов, по существу, эквивалентно образованию такого же объема за счет (равновесных) средних смещений атомов.

Таблица 3. Параметры модели возбужденного состояния для халькогенидных стекол

Стекло, ат. %	к	Л	Л	Jv,, E’	Де,	Д	дн„ кДж моль	Р.
AsmS^p	302	0.010	0.376	56	0.27	3.8	8	3.3
AsyjSjt,	362	0.022	0.305	29	0.45	2.3	9	3.0
ASiaSll	408	0.024	0.289	27	0.49	2.1	10	3.0
AswSto	453	0.030	0.290	16	0.49	2.1	11	2.8
AsjScijj	3J6	0.021	0.326	21	0.39	2.7	8	2.9
AskSw	353	0.020	0.331	22	0.38	2.8	9	2.9
AS30S70	406	0.031	0.290	15	0.49	2.1	9	2.8
As^Sc^j	456	0.029	0.260	18	0.57	1.8	11	3.0
ASmiSCso	442	0.024	0.300	24	0.46	2.3	li	2.9

С этих же позиций подойдем к понятию «энтропия возбуждения атома» (9), помня, что она является характеристикой неравновесного структурного превращения (типа гетерофазной флуктуации плотности) в области стеклования.

Таблица 4. Доля флуктуационного объема f_s, коэффициент Пуассона д и степень неравновеености р, для сульфатнофосфат-ных стекол NaPCE-RSOj (R-Zn, Li, Na, К) (использованы данные [8])

rso4, мол. %	T$, К	к	Л	Jy, У	Дт,, Е’	кДж моль	А
NaPO,	523	0.016	0.294	0.48	16		3.4
ZnSO4- 10	493	0.018	0.288	0.49	12	13	3.3
20	505	0.019	0.284	0.50	12	14	3.3
30	510	0.020	0.273	0.53	11	14	3.3
40	515	0.020	0259	0.27	10	14	3.3
LiSOj - IC	451	0.014	0.300	0.46	13	13	3.5
20	447	0.013	0.303	0.45	14	13	3.5
30	429	0014	0.304	0.45	12	12	3.5
NajSOt— 10	496	0.016	0.299	0.46	14	14	3.4
20	493	0.016	0.292	0.48	15	14	3.4
30	490	0.015	0.288	0.49	17	14	3.5
K2SO4 - 10	444	0.013	0.316	0.42	16	13	3.5
20	453	0.014	0.316	0.42	15	13	3.4

Такому неравновесному изменению структуры системы сопоставимо эквивалентное равновесное структурное изменение типа гомофазной флуктуации плотности. Иными словами, стеклование жидкости будем рассматривать как квазиравно-весный квазифазовый переход, а величины 1/7.,, Дг„ и 1S,. - как характеристики такого перехода.

Полагая, что вероятность рождения возбужденного атома W=N_e/N носит энтропийный характер, и, пользуясь принципом Больцмана, устанавливающим связь между энтропией и вероятностью, можно прийти к основному уравнению модели (1) другим путем [5]

w - ехр--- = ехр--- , Ч к )    ( кТ )

где ДН_е=Т^8_Е - энтальпия возбуждения атома, которая определяется формулой (6).

Таблица 5. Параметры модели возбужденного состояния для аморфных органических полимеров (использованы данные [21])

Поли мер	к		Л	Дь V	Jve, Е1	к2а< моль	А
полипропилен полистирол поли- мепш-метак- рнлат полн- фор-м альдегид поликарбонат полиэтилен	256 363 373 213 420 248	0.32 0.34 0.33 0.31 0.38 0.36	0.035 0.030 0.030 0.037 0.036 0.032	0.41 0.36 0.38 0.43 0.26 0.31	26 39 25 12 33 30	5 7 8 4 7 5	2.5 2.5 2.5 2.5 2.0 2.3

Температура стеклования большинства аморфных веществ, по крайней мере, у систем одного структурного типа, линейно зависит от давления [19,20]:

dPg ---- to const.

dPg

Поэтому, как следует из соотношений (8), (9) и (12), степень неравновесности стеоа («энтропия возбуждения атома») определяется главным образом флуктуаци- онным объемом 4ve, необходимым для критического смещения атома («неравновесного структурного превращения»)

В —^

Ду, я= const ■ Av,.

Иными словами, можно сказать, что

«энтропия возбуждения атома» характеризует флуктуацию упаковки частиц, создающую необходимое условие для предельного смещения кинетической единицы (для формирования определенной неравновесности).

У кварцевого стекла SiO2 с сеточной структурой и с преимущественно кова лентными межатомными связями флуктуационный объем dve=17E3 существенно больше, чем у щелочносиликатных стекол (Jve=7-10 Е3), и составляет 85 % объема кинетической единицы (zlve/y=0.85), а у последних - 60-70% (табл. 1). Это означает, что для предельной деформации межатомной связи или, что то же самое, для критического смещения (возбуждения) атома в линейноразветвленной структуре щелочносиликатных стекол R2O-SiO2 требуется меньшая флуктуация упаковки соседних частиц (флуктуация плотности), чем в сеточной структуре кварцевого стекла SiO2. Известно, что при введении в SiO2 окислов щелочных металлов R2O структура стекла «разрыхляется» и из сеточной превращается в линейноразветвленную структуру [12]. С ростом содержания R2O флуктуационный объем Ave, необходимый для возбуждения атома, уменьшается (табл. 1). К аналогичным результатам приводит анализ данных для других стеклующихся систем (табл. 2-4)-

Заключение. На основе сравнения модели возбужденного состояния с термодинамической теорией стеклования вводится безразмерная величина Д - степень неравновесности стекла, которая определяется отклонением энтропии стекла (неравновесного состояния) от ее равновесного значения в точке стеклования, где состояния жидкости и стекла неразличимы. У аморфных веществ различной химической природы вблизи Tg наблюдается в первом приближении одинаковая степень неравновесности Pg«const«3. Тем не менее величина pg (хотя и слабо) зависит вполне определенным образом от природы стеклующихся систем. Так, у органических аморфных полимеров она заметно ниже фЙ^2.5), чем у неорганических стекол (Д^З). При возрастании содержания мышьяка As с 10 до 40 ат.% в халькогенидных стеклах As-S степень неравновесности падает с 3.3 до 2.8. При этом происходит переход от преимущественно линейной (AS10S90) к трехмерноувязан ной структуре (As^S^). Процесс возбуждения кинетической единицы - ее критическое смещение из равновесного в неравновесное положение, соответствующее максимуму силы межмолекулярного притяжения, можно притяжения, можно рассматривать как «неравновесное структурное превращение» в термодинамической теории стеклования [3].