Модель взаимодействия источников тепла в двухфазной высокотеплопроводной среде

где W, Вт - мощность источника тепла; R, м - радиус образовавшейся при охлаждении твердой фазы калориметрической среды; l, м - длина канала охлаждения; р м и L _Kp -плотность твердой фазы и скрытая теплота кристаллизации калориметрической среды; J = c _p А Т В G _B T - энтальпия охлаждающей среды ( с р – удельная теплоемкость, А Т В -подогрев, G _В , кг / с - расход охладителя и Т, с - время охлаждения конструкции).

При испытаниях можно выделить три этапа формирования твердой фазы из калориметрической среды. Первый этап – от начала поступления охладителя в каналы системы охлаждения до момента наступления контакта профилей твердой фазы; второй – с момента наступления контакта профилей до образования плоского профиля; третий – до полного слияния соседних профилей, то есть потере распознания соседних каналов охлаждения. На втором и третьем этапах испытаний из-за взаимодействия соседних источников тепла образуется переохлажденная область твердой фазы, которая приведет к искажению её профиля, которое выражается дополнительным образованием твердой фазы на внешней поверхности её профиля в области между основными каналами системы охлаждения. При этом масса искажающей твердой фазы определяется выражением

М_и = 0,5 R2 р м ( а - sin a ) l , (2) где a – количество тепла, искажающее локальную картину поля тепловых потоков, в конструкции определится из выражения

Q = L kp M „ = 0,5 R2 р м L kp ( а - sin a ), (3) где а,рад - центральный угол сегмента перекрытия профиля твердой фазы.

Анализ результатов испытаний охлаждаемой конструкции с учетом полученных выражений (1…3) позволяет оценить адекватность измеренных и фактически действующих тепловых потоков, повышая точность их определения [1].

В соответствии с этим методом [1] специально подготовленный объект исследования погружается в ванну с расплавленным высокотеплопроводным чистым металлом и при температуре кристаллизации последнего продувается изнутри воздухом. На поверхности испытуемого объекта при этом образуется твердая фаза термостатирующего металла (металлограмма), толщина которой эквивалентна количеству отведенного с поверхности объекта тепла, и определяет интенсивность внутренней теплоотдачи к воздуху.

Данный способ используется как для определения средне интегральных, так и локальных характеристик теплообмена в оболочковых конструкциях.

Однако, в последнем случае достоверность полученных результатов во многом определяется временем продувки объекта охлаждающим воздухом. Если это время слишком мало, то процессы теплоотдачи носят явно выраженный нестационарный характер и полученная металло-грамма не может быть расшифрована с помощью зависимостей справедливых для стационарного процесса.

При чрезмерно большом времени продувки стационарность явления не вызывает сомнения, но из-за тепловых растоков по корке металла, вызванных тепловым взаимодействием локальных источников тепла, которыми могут быть, например, ребра, формирующие тракт охлаждения, профиль металлограммы сглаживается и в пределе становится сферическим. Это значительно затрудняет, а в ряде случаев делает совсем не возможным определение локальных тепловых характеристик указанным способом.

Целью данной работы являлось создание простейшей математической модели процесса образования металлограммы при калориметрических исследованиях охлаждаемых оболочковых конструкций в жидкометаллическом термостате, которая может быть использована при назначении одного из основных режимных параметров испытания – времени продувки объекта воздухом, а также при расшифровке металлограмм.

При этом задача формулируется следующим образом. Дана гладкая не теплопроводящая бесконечная поверхность, на которой параллельно расположены на расстоянии X друг от друга два бесконечно протяженных отрицательных источника тепла одинаковой мощности q . Эта поверхность находится в идеальном тепловом контакте с расплавленным металлом термостата, находящимся при температуре кристаллизации.

Необходимо найти математические выражения, описывающие профиль металлограммы на различных этапах действия таких источников тепла. Схемы для решения поставленной задачи приведены на рис. 1.

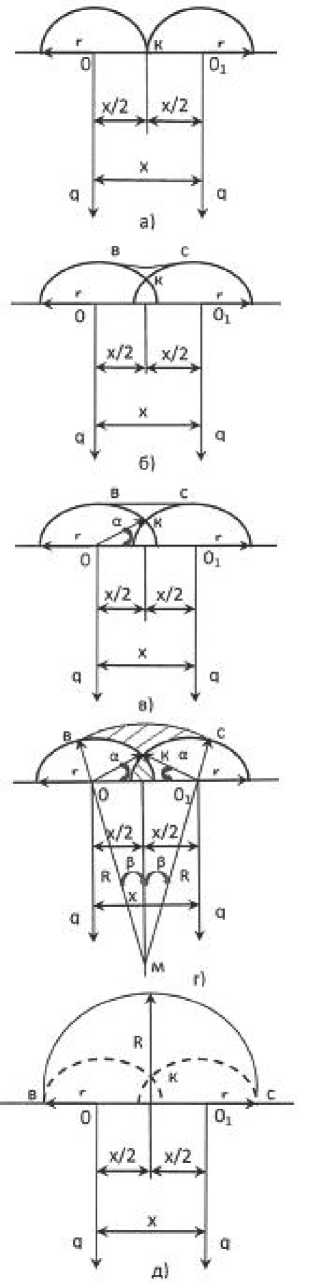
Рис.1. Схема изменения профиля металлограммы при взаимодействии источников тепла

До определенного времени источники тепла не взаимодействуют, друг с другом, поэтому на поверхности стенки, контактирующей с расплавом термостатирующего металла, будет нарастать твердая фаза металла, профиль которой соответствует двум прямым круговым цилиндрическим поверхностям переменного радиуса r . Величина r зависит от времени т действия источников. При увеличении т цилиндрические поверхности корки сближаются и в некоторый момент времени т кр 1 смыкаются на исследуемой стенке (рис. 1, а). С этого времени начинается взаимное влияние источников тепла друг на друга, так как переток тепла по твердой фазе приводит к искажению фронта кристаллизации и на металлограмме появляется область “ в-с ” (рис. 1, б).

В последующие моменты времени профиль нарастающей корки искажается и приходит к виду, показанному на рис. 1, в, соответствующий этому момент времени т кр 2 . Начиная с этого момента времени на профиле корки нет явно выраженных максимумов её толщины, которые определяли ранее местоположение источников тепла на поверхности стенки. Однако, в этот момент времени ещё можно точно идентифицировать положение источников тепла, которое будет соответствовать линиям сопряжения (“ в ” и “ с ”) цилиндрической и плоской поверхностей профиля твердой фазы. При дальнейшем увеличении времени действия источников плоская поверхность (“ в-с ”) профиля металлограммы становится криволинейной (рис. 1, г).

Точки сопряжения (“ в ” и “ с ”) её с круговой цилиндрической поверхностью профиля всё менее соответствуют местоположению источников тепла на поверхности стенки. В момент времени т кр з точки “ в ” и “ с ” достигают поверхности стенки. При этом профиль корки представляет собой прямой круговой цилиндр радиуса R (рис. 1, д), что эквивалентно действию источника тепла удвоенной мощности помещенного на расстоянии 0,5 X между рассмотренными источниками тепла, т.е., начиная с т кр 3 данным методом нельзя определить на расстоянии X действует один или два источника тепла.

Для определения профиля металлограммы, соответствующего различным моментам времени можно использовать принцип суперпозиции. При этом для построения профиля использовались круговые цилиндрические профили метал-лограмм независимых источников, а окончательный профиль находился из условия равенства совмещенной площади S₂ и площади S₁ корректирующей профиль металлограмм невзаимодействующих источников.

В результате аналитического анализа получены следующие выражения. Для момента вре- мени начало взаимодействия источников тепла (рис. 1, а):

^Гкр 1 ^{— 0,5} х .

Для момента времени т кр ₂ , как следует из рис. 1, в:

xr x tga

D i —---

₂ 90 - a то г ---------,

S 2

7 .            7 .

то- a х tg a

.

Из условия 5 1 — 5 2 следует, что r ₂ — —. ^р то

При ^т ^ ^т кр 2 (рис. 1, ^г):

„      2В    2 90-а + В х2

5. — to R ²-- 2 то г ²--- tg a —( R - r )cos B ,

1      360         360     42

то г ² a x ² tg a

D o —.

2    1804

Приравняем два последних выражения 5 1 — 5 ₂ , т.е.

(R2 - r2)В--(R - r)cosВ — 90r2, то где В — arcsin--------.

2( R - r )

Если В — 90 0 ; R — r + 0,5 x ; (рис. 1 .д), то из условия 5 ₁ — 5 ₂ следует, что:

Г кр 3 — 0,5(1 + V2),            (5)

0,5тог 2 lpL — qFт,

r —

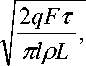
где р и L - плотность и удельная теплота кристаллизации термостатирующего металла; l – протяженность источника тепла; F – площадь поверхности стенки, занятая источником тепла; q - мощность источника тепла; т - время действия источника тепла.

С учетом выражений (4…5), из уравнения (6) получим:

^т кр 1

1 to x ² l p L

8 qF ^,

т кр2

1 to x ² l p L 4,928 qF ^,

т кр1

1 to x ² l p L

1,368 qF ^,

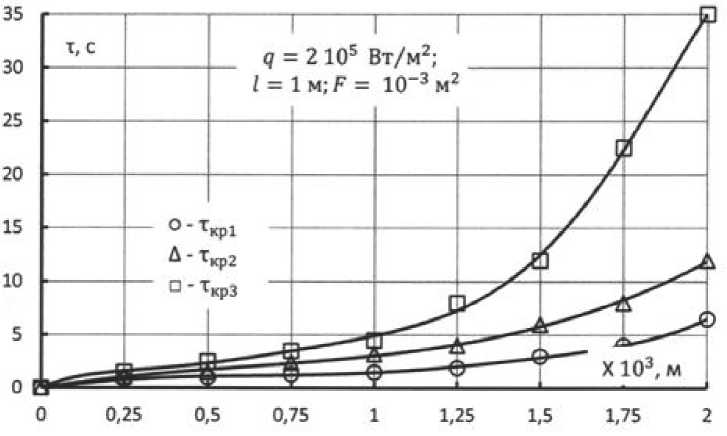
Рис. 2. Динамика разрешающей способности калориметрирования охлаждаемых конструкций

При использовании калориметрического способа в качестве жидкометаллического теплоносителя обычно используется цинк, для которого р = 7100 кг/м ³ , L = 98,3 - 10 ³ Дж/кг . Если известны также мощность, их протяженность и площадь, то для различных значений расстояний “х” между источниками можно построить с помощью выражений (7...9) зависимость т = f ( x ) . Например для q = 2 - 10 ² Вт/м ² , l = 1 м , F = 1 - 10 ³ м ³ такая зависимость имеет вид представленный на рис. 2.

Как видно из рис. 2, взаимодействие источников тепла, находящихся на расстоянии 2 - 10 3 м , начинается через ~ 5,5 с ; а через ~ 32 с , такие источники становятся практически не различимы на металлограмме. Поэтому временной интервал испытаний для данных условий не должен превышать = 32 с .

Следует отметить, что в натурном эксперименте кроме рассмотренных факторов на формирование корки оказывают влияние такие явления, как теплопроводность стенки, на которой размещены источники тепла; наволакивание жидкой фазы, возникающее при выемке объекта из термостатирующей среды после окончания продувки. Такие процессы приводят к сокращению указанных временных интервалов испытаний в жидкометаллическом термостате.

Предложенная модель проверена экспериментально и может быть использована в практике планирования калориметрического эксперимента.