Модель взаимодействия зондирующего потока СВЧ преобразователя с элементами зубчатого колеса

Диагностика и контроль рабочего состояния редукторов и зубчатых передач контактными и бесконтактными методами в настоящее время осуществляется, в основном, в статическом состоянии. Основными недостатками «статической» диагностики являются: необходимость препарирования механизма, влекущая за собой увеличение трудоемкости процесса диагностики, и невозможность постоянного мониторинга рабочего состояния зубчатого колеса в реальном времени. Известные методы диагностики зубчатых передач в динамическом эксплуатационном режиме, например, вибродиагностика позволяют судить о рабочем состоянии контролируемого объекта только по косвенным признакам, поэтому не позволяют идентифицировать область износа конкретного зубца и определять его количественную оценку. Таким образом, объективный контроль технического состояния редукторов в эксплуатационном режиме, позволит проводить мониторинг энергонагруженных редукторов, вести паспорт зубчатых колес и эксплуатировать зубчатые механизмы по их техническому состоянию.

Цель работы – разработка математической модели процесса взаимодействия зондирующего потока и объекта исследования, для теоретического обоснования и описания разрабатываемого метода.

В статье рассматривается бесконтактный метод контроля рабочего состояния зубчатого колеса, основанный на обработке в реальном времени сигналов, полученных после детектирования отраженного от зубцов колеса зондирующего СВЧ излучения. Параметры информационных сигна-

лов сравниваются, соответственно, с эталонными, полученными в начале эксплуатации зубчатого колеса. Данный метод позволяет получать информацию непосредственно о степени изношенности каждого конкретного зубца и появлении в нем дефектов [1].

В результате проведенных экспериментов с волноводными СВЧ преобразователями было выяснено, что информационный сигнал после детектирования отраженного зондирующего СВЧ излучения, будет иметь форму колоколообразного импульса. Установка для проведения эксперимента представлена на рис.1.

Рис. 1. Установка для проведения экспериментов с волноводными СВЧ преобразователями

Исследование возможностей и определение граничных условий реализации метода контроля рабочего состояния зубчатого колеса приводят к необходимости теоретического обоснования и описания разрабатываемого метода, т.е. разработки математической модели процесса взаимодействия зондирующего потока и объекта исследования - зубчатого колеса. Процесс создания математической модели можно условно разбить на два этапа, определяющих ее усложнение с целью повышения достоверности метрологических характеристик получаемых результатов. Усложнение модели взаимодействия зондирующего потока и контролируемого объекта – это переход к построению модели в трехмерной системе координат, что в свою очередь дает возможность моделирования и учета таких пространственных дефектов как раковины, сколы и продольные трещины, которые в линейной модели не учитываются. Итак, первый этап - построение модели в двумерной системе координат. Модель строится на законах геометрической оптики.

В разрабатываемом бесконтактном методе важен процесс информационного взаимодействия зондирующего потока приемно-передающих элементов первичного СВЧ преобразователя с поверхностью зубца. Поэтому можно упростить построение модели и рассматривать описание не всей шестерни, а только ее отдельного зубца. Влияние среды между приемно-передающими элементами СВЧ преобразователя и контролируемым объектом на информационные параметры их взаимодействия в математической модели учитываться не будет. В качестве упрощенной модели зубца шестерни выбирается трапеция.

Первичный преобразователь представляет собой цилиндрический волновод с диэлектрическим заполнением (см. рис. 1), торец которого является одновременно и излучателем и приемником, поэтому представляется в модели совокупностью приемных и передающих элементов. При работе устройства в волноводной системе преобразователя устанавливается стоячая волна, параметры которой изменяются в результате воздействия отраженного от зубцов зондирующего СВЧ излучения.

Отраженное СВЧ излучение, в свою очередь зависит от различных параметров отражающей поверхности, в данном случае интересны ее геометрические параметры. Приемно-излучающий торец волновода имеет форму круга и при построении модели в двумерной системе координат торец первичного преобразователя проецируется в отрезок, каждая точка которого является и излучателем и приемником, так же как и у торца волновода.

Изменяя положение зубца относительно излучателя, можно наблюдать изменение выходного сигнала при различных вариациях положения приемно-передающих элементов преобразователя относительно контролируемого зубчатого колеса. На рис. 2 показаны модели зубца и излучателя. Эти модели описываются набором линейных функций с граничными условиями, представленными в выражении 1. Функции y1 – y5 описывают зубец, а функция y6 излучатель. На рис.2 показаны точки A, B, C, D, E, F, G, K, для которых устанавливаются граничные условия. Изменяя эти функции и граничные условия можно моделировать различные варианты расположения излучателя относительно зубчатого колеса, износ зубьев, а так же различные формы зубьев. Механизм взаимодействия лучей зондирующего потока приемно-передающих элементов преобразователя с исследуемой поверхностью проиллюстрирован на рис. 3.

y i = kx + b_v ^{[ x} A ; x B ^]

y 2 = k 2 x + b 2 , [ X b ; X c ]

y ₃ = k ₃ x + b ₃, [ x c ; x d ] y ₄ = k 4 x + b 4 , [ X d ; X e ] y ₅ = k ₅ x + b ₅, [ X e ; X f ] y ₆ = const , [ X g ; X k ]

Из каждой точки излучения приемно-передающего торца преобразователя, в пределах линейного угла, определяемого диаграммой направленности излучателя, выходят лучи с определенным угловым шагом. Выбор шага определяет необходимую точность представления протекающих процессов взаимодействия зондирующих лучей с контролируемой поверхностью. В качестве примера для дальнейшего описания механизма взаимодействия используется луч 1 (рис. 3.) Для учета интенсивности каждого зондирующего и отраженного луча используется соответствующий весовой коэффициент, определяемый их угловым положением в диаграмме направленности датчика. Весовой коэффициент уменьшается с увеличением угла падения относительно нормали к приемно-излучающему торцу датчика.

Затем исследуются и определяются точки пересечения зондирующих лучей с поверхностью зубца. После этого устанавливается соответствие точек пересечения граничным условиям, приведенным в выражении 1. Если точка пересечения попадает в диапазон существования, который обозначен граничными условиями, то она используется в дальнейших вычислениях, если нет, то отбрасывается. Из точек пересечения восстанавливаются нормали к исследуемой поверхности. На рис. 3 – это перпендикуляр 2 для луча 1. Для этого используется формула 2.

, 1

knep =- k ■ <²>

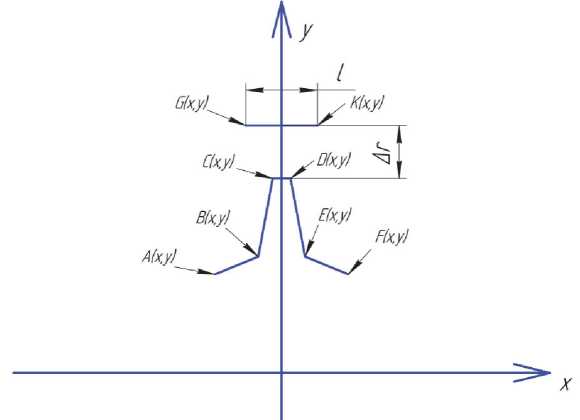
Рис. 2. Линейные модели излучателя и зубца

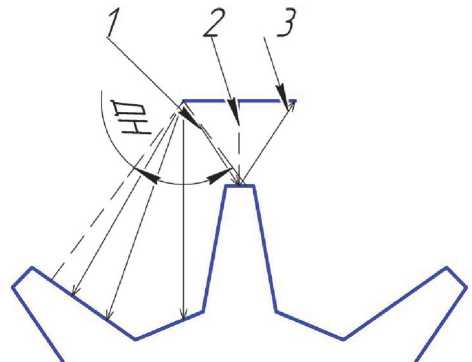
Рис. 3. Механизм взаимодействия лучей зондирующего потока приемно-передающих элементов преобразователя с исследуемой поверхностью

После этого строятся отраженные лучи в соответствии с законами геометрической оптики и им присваиваются соответствующие весовые коэффициенты для отраженных лучей. В данном случае это луч 3 на рис. 3. Далее, вычисляются точки пересечения отраженных лучей и приемно-излучающего торца датчика. Каждая точка пересечения отраженного луча и торца датчика исследуется на соответствие граничным условиям. Если точка соответствует граничным условиям, то она используется при дальнейших вычислениях, если нет, то отбрасывается.

Следующим шагом выполняется поворот зубца относительно начала координат на определенный шаг, заданный заранее, это происходит с помощью формул (3) поворота графика функций относительно зависимостей, описывающих геометрию зубца:

x_S = x cos ф - y sin ф ; y_s = x sin ф + y cos ф .

После осуществления математической процедуры поворота, повторяются операции с лучами, описанные выше. Для вычисления нового углового коэффициента применяется выражение 4.

k s = У ' s .                    (4)

Количество отраженных и принятых лучей с учетом их весовых коэффициентов позволяет получить мгновенное значение выходного сигнала первичного преобразователя в определенный момент времени, который связан с угловым положением зубца относительно датчика. Совокупность всех мгновенных значений – формирует вид и форму выходного сигнала, характеризующего параметры поверхности конкретного зубца шестерни.

ВЫВОДЫ

Построение математической модели позволяет:

• -    создать теоретическое обоснование результатов практического эксперимента;

• -    обосновать выбор рационального взаимного

расположения датчика и зубцов исследуемого зубчатого колеса.

Кроме этого, математическая модель взаимодействия зондирующего излучения с контролируемой поверхностью зубца в двухмерной системе координат позволит в дальнейшем перейти к построению информационно более емкой модели в пространстве.