Модели и алгоритмы автоматической группировки объектов на основе модели k-средних

Введение. Автоматическая группировка (АГ) предполагает разделение множества объектов на подмножества (группы) так, чтобы объекты из одного подмножества были более похожи друг на друга, чем на объекты из других подмножеств по какому-либо критерию. В процессе группировки объектов некоторого множества на определенные группы (подмножества) учитываются общие признаки объекта и методы, с помощью которых происходило разделение.

Чтобы исключить появление ненадежных электрорадиоизделий, предназначенных для установки в бортовую аппаратуру космического корабля с длительным периодом активного существования, вся электронная компонентная база проходит через специализированные центры технических испытаний [1; 2]. Эти центры выполняют операции полного входного контроля электрорадиоизделий, дополнительные проверочные тесты, диагностического неразрушающего контроля и выборочного разрушающего физического анализа.

Обнаружение исходных однородных производственных партий электрорадиизделий из отгруженных партий является важных этапом во время тестирования [1].

Одной из наиболее известных моделей кластерного анализа является модель k-средних. Целью является нахождение k точек (центров) X 1 ,…X k в d -мерном пространстве, таких, чтобы сумма квадратов расстояний от известных точек (векторов данных) A 1 ,…,A N до ближайшей из искомых точек (центров) достигала минимума [3]:

argmin F ( X ₁,..., X_k ) = ∑ _i ^N _{= 1}m in X_j - A_i II² . (1)

В алгоритме k-средних необходимо первоначально спрогнозировать количество групп (подмножеств). Кроме того, полученный результат зависит от начального выбора центров. А также функция расстояния и ее определение играют важную роль в проблеме разделения исследуемого множества на группы.

Первый генетический алгоритм решения дискретной задачи p-медианы был предложен Хосейджем и Годшильдом [4]. Алгоритм [5] дает довольно точные результаты. Однако скорость сходимости целевой функции происходит очень медленно. В своей работе О. Алп, Э. Эркут, Ц. Дрезнер [6] представили более быстрый простой генетический алгоритм с особой процедурой рекомбинации, которая также дает точные результаты. Данные алгоритмы решают дискретные задачи. Авторы работы «Метод кластеризации на основе генетического алгоритма» [7] кодируют решения (хромосомы) в своих ГА как наборы центроидов, представленных их координатами (векторами действительных чисел) в многомерном пространстве.

Анализ литературы показал, что существующие решения в области АГ многомерных объектов обладают либо высокой точностью, либо обеспечивают стабильность результата при многократных запусках алгоритма, либо высокой скоростью работы, но не всеми этими качествами одновременно. На сегодняшний день разработаны алгоритмы k-средних и k-медиан лишь для наиболее распространенных мер расстояния (евклидово, манхэттенское). Однако, учет особенностей пространства признаков конкретной практической задачи при выборе меры расстояния может привести к повышению точности АГ объектов. В представленной работе в качестве меры точности кластеризации используем индекс Рэнда (Rand Index, RI) [8].

Улучшить результат АГ многомерных объектов с повышенными требованиями к точности и стабильности результата известными алгоритмами на текущий момент крайне трудно без значительного увеличения временных затрат. При решении практических задач АГ многомерных данных, например, при решении задач выделения однородных партий промышленной продукции, вопросы вызывает адекватность моделей и, как следствие, точность АГ промышленной продукции. Все же возможна разработка алгоритмов, обеспечивающих дальнейшее улучшение результата на основе выбранной модели, например, модели k-средних.

В многомерном пространстве признаков зачастую существует корреляция между отдельными признаками и группами признаков. Использование корреляционных зависимостей может быть задействовано путем перехода от поиска в пространстве с евклидовой или прямоугольной метрикой к поиску в пространстве с метрикой Махаланобиса [9-11]. Квадрат расстояния Махаланобиса D M определяется следующим образом:

D M ( X ) = ( X - µ ) ^TC ^{- 1}( X - µ ) (2) где X – вектор значений измеренных параметров, µ – вектор средних значений (например, центр кластера), С – ковариационная матрица.

Целью исследования в представленной работе является повышение точности и стабильности результата решения задач автоматической группировки объектов.

Идея работы состоит в том, чтобы использовать меру расстояния Махаланобиса c усредненной оценкой ковариационной матрицы в задаче k-средних для снижения доли ошибки АГ по сравнению с другими известными алгоритмами, а также задействовать оператор мутации в составе генетического алгоритма для повышения точности и стабильности решения по достигаемому значению целевой функции за фиксированное время выполнения по сравнению с известными алгоритмами разделения объектов.

Исходные данные . Исследование проведено на данных тестовых испытаний партий интегральных схем [12], предназначенных для установки в аппараты космического назначения, проведенных в специализированном центре технических испытаний. Данные представляют собой набор параметров электрорадиоизделий (ЭРИ). Исходная партия ЭРИ принадлежит разным однородным партиям, в соответствии с маркировкой производителя. Общее количество изделий составляет 3987 изделий. В каждой партии изделие описывается 205 измеряемыми параметрами. Партия 1 содержит 71 изделие, 116 изделий содержится в партии 2, 1867 в партии 3, 1250 в партии 4, 146 в партии 5, 113 в партии 6, 424 в партии 7.

Алгоритм k-средних с расстоянием Махаланобиса с усредненной оценкой ковариационной матрицы по обучающей выборке. Вычислительные результаты экспериментов по автоматической группировке промышленной продукции с моделями k-медоид и k-средних, в которых применена метрика Махаланобиса, показывают повышение точности кластеризации при автоматической группировке на 2-6 кластеров и малом количестве объектов и информативных признаков [13].

Предложено вместо ковариационной матрицы из (2) по обучающей выборке рассчитать усредненную оценку ковариационной матрицы для однородных партий изделий (по предварительно размеченным данным):

k

C = - Z j                       (3)

ⁿ j = 1

где n j - количество объектов (изделий) в j -й партии, n-общий размер выборки, C j -ковариационные матрицы отдельных партий изделий.

В данной работе предложен алгоритм автоматической группировки объектов, основанный на модели k-средних с подстройкой параметра меры расстояния Махаланобиса (ковариационной матрицы) по обучающий выборке:___________________________________ Алгоритм 1. k-средних с расстоянием Махаланобиса с усредненной оценкой ковариационной матрицы

Шаг 1. Методом k-средних с евклидовым расстоянием разделить выборку на некоторое число к кластеров (здесь к - некоторая экспертная оценка возможного числа однородных групп, не обязательно точная);

Шаг 2. Для каждого кластера рассчитать центр ц , . Центр определяется как среднее арифметическое всех точек в кластере

M i =~ Z ^Х л m j = 1

где m - количество точек, X j - вектор значений одного измеряемого параметра (j= 1 ..m );

Шаг 3. Рассчитать усредненную оценку ковариационной матрицы (3). Если усредненная оценка ковариационной матрицы является вырожденной, перейти к шагу 4, иначе перейти к шагу 5;

Шаг 4. Увеличить число кластеров на (к+1) и повторить шаги 1 и 2. Сформировать новые кластеры с квадратом евклидова расстояния:

n

D ( X, , ц ) = Z ( X ,- ц , )²                              (5)

i = 1

где n - количество параметров. Вернуться к шагу 3 с новым обучающим примером (набором).

Шаг 5. Сопоставить каждую точку ближайшему центроиду, используя квадрат расстояния Махаланобиса (2) с усредненной оценкой ковариационной матрицы С (3) для формирования новых кластеров.

Шаг 6. Повторить алгоритм с шага 2, пока кластеры не перестанут изменяться.

В работе представлены результаты трех групп экспериментов по данным образцов промышленной продукции.

Первая группа. Обучающая выборка соответствует рабочей выборке, для которой проводилась кластеризация.

Вторая группа. Обучающая и рабочая выборки не совпадают. На практике в качестве обучающей выборки тестовый центр может использовать ретроспективные данные поставок и тестирования изделий того же типономинала.

Третья группа. Обучающая и рабочая выборка также не совпадает, но в качестве обучающей выборки использовались результаты работы автоматической группировки изделий (k-средних в режиме мультистарта с евклидовой метрикой).

В каждой из групп экспериментов для каждой рабочей выборки алгоритм к-средних запущен по 30 раз с каждой из пяти исследуемых моделей кластеризации.

Модель DM 1 – k-средних с расстоянием Махаланобиса, ковариационная матрица рассчитана для всей обучающей выборки.

Модель DС – k-средних с расстоянием, аналогичным расстоянию Махаланобиса, но используется корреляционная матрица вместо ковариационной матрицы.

Модель DM 2 – k-средних с расстоянием Махаланобиса, с усредненной оценкой ковариационной матрицы.

Модель DR – k-средних с манхэттенским расстоянием.

Модель DE – k-средних с евклидовым расстоянием.

Таблица 1

Результаты вычислительного эксперимента над данными микросхемы 1526IE10_002 (3987 векторов данных размерностью 68), обучающая выборка состоит из 10 партий, Третья группа, рабочая выборка составлена из 7 партий изделий)

Серия V	индекс Рэнда (RI)					Целевая функция
	Модель					Модель
	DM1	DС	DM2	DR	DE	DM1	DС	DM2	DR	DE
Max	0,767	0,658	0,749	0,740	0,735	255886	379167	281265	18897	6494,62
Min	0,562	0,645	0,696	0,703	0,705	250839	36997	274506	17785	5009,42
Average	0,632	0,650	0,725	0,714	0,719	252877	37178	277892	18240	5249,95
Std .Dev	0,047	0,003	0,016	0,008	0,006	1164,5	152,8	2358,9	452,7	366,5
V						0,461	0,411	0,849	2,482	6,981
R						5047	920	6759	1112	1485

Установлено, что новая модель DM2 с усредненной оценкой ковариационной матрицы показывает лучшую точность среди представленных моделей практически во всех сериях экспериментов по индексу Рэнда (RI) и во всех случаях превосходит модель DE, где используется евклидово расстояние. Также в экспериментах показано, что в большинстве случаев коэффициент вариации значений целевой функции выше для модели DE, где используется евклидова мера расстояния, а также, что коэффициент размаха значений целевой функции имеет самые высокие значения для модели DM2, где используется мера расстояния Махаланобиса с усредненной оценкой ковариационной матрицы. Следовательно, для получения устойчиво хороших значений целевой функции требуются множественные попытки запуска алгоритма k-средних или использование других алгоритмов, основанных на модели k-средних (например, j-means [14] или алгоритмов метода жадных эвристик [15]).

Генетический алгоритм с перекрестной мутацией для задачи k-средних . Новый алгоритм позволяет повысить точность решения задачи k-средних и стабильность результата за фиксированное ограниченное время выполнения. В данной главе под точностью алгоритма будем понимать исключительно достигнутую величину целевой функции, не учитывая показатели адекватности модели и соответствие результатов алгоритма фактическому (реальному) разделению объектов, если таковое известно.

Для генетических алгоритмов решения задачи k-средних с вещественным кодированием решений известно очень ограниченное множество возможных операторов мутации. Например, авторы работы «Метод кластеризации на основе генетического алгоритма» [7] кодируют решения (хромосомы) в своих ГА как наборы центроидов, представленных их координатами (векторами действительных чисел) в многомерном пространстве. Каждая хромосома подвергается мутации с фиксированной вероятностью д . Процедура (оператор) мутации заключается в следующем.

Алгоритм 2 3.1 Процедура исходной мутации ГА для задачи k-средних

Шаг 1 . Генерация случайного числа b е (0,1] с равномерным распределением;

Шаг 2.ЕСЛИ Ь<д, ТО хромосома мутирует. Если положение текущего центроида и, то после мутации оно становится:

и ^1

и ± 2 х bхи, и * 0,

и ± 2 х b ,

и = 0.

Знаки «+» и «-» имеют одинаковую вероятность. Координаты центроида смещены случайным образом.

В своей работе мы заменили эту процедуру мутации для задачи k-средних следующей процедурой.

Алгоритм 3 3.2 Процедура перекрестной мутации ГА для задачи k-средних

Шаг 1. Генерация случайного начального решения S = { X i ... X k };

Шаг 2. Применить алгоритм k-средних к S для получения локального оптимума S ;

Шаг 3. Применить простую перекрестную процедуру для мутированного индивида S из популяции и S для получения нового решения S^’’ ;

Шаг 4. Применить алгоритм k-средних к S для получения локального оптимума S ;

Шаг 5.ЕСЛИ F ( S ”)< F ( S ' ), ТО S ' ^ S ”. _____________________________________________

Предложенная процедура используется с вероятностью мутации равной 1, после каждого оператора скрещивания.

Результаты запуска исходного алгоритма 2, описанного с вероятностью мутации 0,01, и его версия с алгоритмом 3 в качестве оператора мутации представлена на рисунке (численность популяции N pop = 20 ). Новая процедура мутации является быстрой и эффективной по сравнению с исходной мутацией генетического алгоритма, показана высокая скорость сходимости целевой функции.

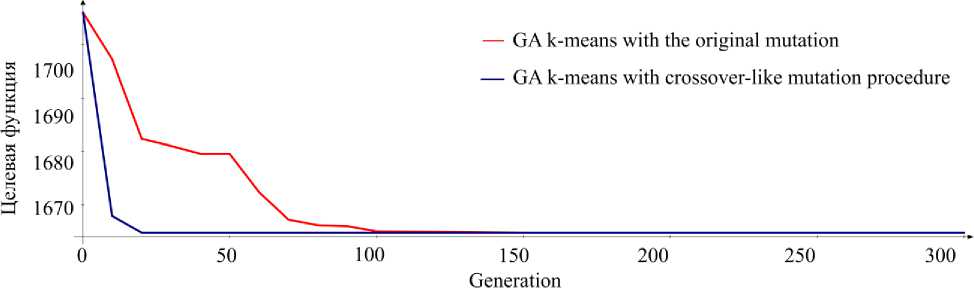
Результаты для набора данных Mopsi-Joensuu (6014 векторов данных размерностью 2), 300 кластеров, 3 минуты

Results for data set Mopsi-Joensuu (6014 data vectors of dimension 2), 300 clusters, time limition 3 minutes

Генетические алгоритмы метода жадных эвристик и многие другие эволюционные алгоритмы для задачи k-средних, обходятся без мутации. Идея жадной агломеративной эвристической процедуры заключается в объединении двух известных решений в одно недопустимое решение с избыточным числом центроидов и далее последовательно уменьшается количество центроидов. На каждой итерации удаляется центроид, который показывает наименьшее увеличение значения целевой функции (1).

Алгоритм 4. Базовая жадная агломеративная эвристическая процедура

Дано : начальное число кластеров K , необходимое количество кластеров k, k, начальное решение S= {X,...,X }, где |S|=K.

ШАГ 1. Улучшить начальное решение алгоритмом k-средних

ПОКА K>k

ЦИКЛ для каждого i ^' ∈ {1, K} выполнить:

ШАГ 2. S ^' ← S { X ^'}. Улучшить решение S^’ алгоритмом k-средних и сохранить соответствующие полученные значения целевой функции (1), как переменные F i ^' ← F { X ^'}.