Модели и алгоритмы искусственного размножения данных для обучения алгоритмов распознавания лиц методом Виолы-Джонса

Одной из важных задач, которые приходится решать при построении алгоритмов машинного обучения, является формирование обучающей выборки, содержащей множество образов анализируемых объектов. Их поиск и подготовка к использованию часто требуют значительных затрат времени и ресурсов. В ряде случаев сбор необходимого числа таких образов оказывается сложен или даже невозможен из-за специфического характера предметной области.

Решение данной задачи особенно актуально для систем распознавания объектов на изображениях и, в частности, распознавания лиц, базирующихся на реализации современных методов построения алгоритмов машинного обучения. С учетом необходимости обеспечения представительности обучающих данных одним из возможных подходов является искусственное размножение некоторых «опорных» образов на основе стохастических или детерминистских моделей преобразования.

В ряде исследований, например, [1, 2], метод искусственного размножения применяется при работе с несбалансированными обучающими выборками с малым числом примеров. В данных выборках образы одного класса (необязательно речь идет об изображениях) значительно превалируют над образами другого. При этом классы уравновешиваются за счет искусственной генерации новых значений признаков входящих в них элементов на основе результата оценки их статистических параметров, проведенной для исходной выборки.

Также известным подходом в задачах распознавания изображений, связанных с обнаружением объектов в естественной среде, является размножение обучающей выборки за счет искажения перспективы или

Целью данной работы является обоснование и исследование различных моделей искусственного размножения обучающих данных на основе внесения деформирующих искажений (ДИ) в цифровые изображения подлежащих детектированию и имеющих явно выраженные структурные характеристики объектов, а также анализ возможностей применения подобного подхода на примере алгоритма распознавания лиц по методу Виолы–Джонса [4, 5].

Данный алгоритм был выбран в качестве инструмента исследования как один из самых надежных и популярных на данный момент детекторов фронтальных лиц [6]. Метод основан на применении комплекса взаимосвязанных подходов и технологий, в центре которых лежит идея построения точного или, как еще говорят, сильного классификатора путем комбинирования других менее точных или слабых классификаторов [7]. Как и большинство других методов машинного обучения, метод Виолы–Джонса требует подготовки большого набора обучающей выборки. В качестве инструмента при проведении исследований авторами был использован разработанный ими в среде Matlab с применением технологии CUDA алгоритм распознавания, содержащий в себе параллельные реализации как процесса обучения, так и процесса принятия решений [8].

1.    Математическая модель внесения деформирующих искажений

Математическая модель процесса внесения ДИ для любой исходной функции f ( x 1 ,…, x n ) от n переменных определяется следующим соотношением:

f( Х 1 + r₁( x 1 ,..., x n ),..., x n + r n ( x 1 ,..., x n )) =

= f(U i ( X 1 ,..., X n ),...,u n ( X 1 ,..., X n )) = g( X 1 ,..., X n ),

где g( x 1 ,..., X n ) - результирующая деформированная функция; r i ( x 1 ,., x n ), i = 1, n - функции вносимых деформирующих искажений по каждой координате, которые могут носить детерминированный или стохастический характер. Используя ранее введенные обозначения, а также введя векторы x = ( x 1 ,., x n ) T , r( x ) = (n( x ),.,r n ( x )) T и u ( x ) = (u 1 ( x ),.,u n ( x )) T , можно записать

^{f( x + r ( x ))} = ^f( u ^{( x ))} = g^{( x )}. ⁽²⁾

При реализации процесса внесения ДИ на основе (1) и (2) возникает ряд особенностей [9]. Первая из них: для того, чтобы значение деформированной функции g( x ) = f( u ( x )) существовало, область ее определения не должна выходить за пределы области определения исходной функции f( x ), т.е. если для f( x ) вектор x е Q _x , то и вектор u ( x ) е Q _x .

Для обеспечения выполнения условия u ( x ) е Q _x применимы различные подходы. Один из возможных вариантов состоит в том, чтобы при выходе какой-либо компоненты координат в x + r ( x ) = u ( x ) из (2) за границы исходной области определения Q x в качестве значения данной компоненты u ( x ) при расчете f( u ( x )) подставлять граничное значение соответствующей координаты исходной функции f( x ). Преимущество данного подхода состоит в том, что при его применении не ограничиваются значения функции деформации r( x ) в случае, когда x + r ( x ) = u ( x ) находится в пределах Q _х . Именно этот подход был использован в нашей работе.

Вторая особенность процесса внесения ДИ на основе (1) и (2) состоит в следующем. Если исходная функция f( x ) является решетчатой функцией дискретных аргументов, т.е. задана на многомерной дискретной сетке (например, в случае внесения ДИ в цифровые изображения), прямое применение (1) и (2) невозможно; и для обеспечения возможности модификации аргументов ff( x ) при внесении в них ДИ произвольного характера необходимо предварительно выполнить ее интерполяцию и представление в виде функции f( x ) непрерывнозначных аргументов. При этом общая процедура будет соответствовать схеме, представленной на рис. 1.

Утверждение. Пусть: f( x ) - функция, заданная на множестве значений n непрерывных аргументов Q x ; ff( x ) - решетчатая функция, сформированная на многомерной дискретной сетке, покрываемой Q x ; f( x ) -функция, интерполированная на основе значений f( x ) и определенная на Q _x с Q _x ; g( x ) - деформированная функция на основе внесения ДИ r( x ) в f( x ) по формуле (1); g( x ) - деформированная аналогичным образом функция на основе внесения ДИ r( x ) в f( x ) ;

X - некое связное подмножество значений непрерывных аргументов x е X cQ_x . Пусть также для любого x е X выполняется u ( x ) е X .

( Начало )

Регистрация исходной решётчатой функции дискретных аргументов f(x)

Интерполяция f(x) и представление её в виде функции непрерывнозначных аргументов f(x)

Внесение деформации путём подстановки в аргументы f(x) искажений г(х) и получение g(x)

x ^{( j )} = u ( x ), то U = X , так как каждому x ∈ X соответствует свое уникальное значение u ( x ) ∈ U , при том, что по определению U ⊂ X , и в этом случае max |g( x ) - g( x )| = max f( x ) — f ( x )|.

Аналогичным образом можно доказать, что min|g(x) - g(x)| > min|f(x) - f(x)|.

Следствие. Ошибка |g( x ) - g( x )|, возникающая при деформации интерполированной функции f( x ) с областью определения Ω _x , не выйдет за пределы максимального и минимального значения ошибки интерполяции |f( x ) - f ( x )| при условии, что u ( x ) G Si x . Для подтверждения этого следствия достаточно повторить предыдущее доказательство в случае X = Ω _x .

Таким образом, при внесении ДИ достаточно выполнить u ( x ) ∈ Ω _x , что производится при помощи того же описанного выше подхода, что и при обеспечении условия u ( x ) ∈ Ω x . При этом u ( x ) ∈ Ω _x автоматически означает, что u ( x ) ∈ Ω x , так как Ω _x ⊂ Ω _x .

Внесение ДИ в рассмотренной схеме может также производиться и обратным образом:

f(x1) =g(u-1(x1)) =g(x1+ r-1(x1)) , где r–1(x1) – функция деформации, обратная к r(x2), и x1 с x2 такие, что f(x2+ r(x2)) =f(u(x2)) =g(x2), x1 = x2 + r(x2), x2 = x1 +r-1(x1) .

В некоторых публикациях данную технологию можно обнаружить под названием «варпинг» (warping) [10]. Он используется при «морфинге» (morphing) – процессе постепенного замещения одного изображения другим путем плавных изменений положений, схожих по некоему признаку частей этих двух изображений и интенсивностей их пикселей. Основной областью применения подобных технологий является компьютерная графика в кино и анимации.

• 2.    Модели и алгоритмы внесения деформирующих искажений с целью размножения обучающей выборки

При проведении исследования нами были рассмотрены три модели внесения ДИ с целью искусственного размножения обучающих данных.

Первая модель внесения ДИ основана на применении в качестве функции деформации r(x) = r(x, y) = {ri(x, y),i = 1,2} , гармонических функций (ГФ) вида ri(x,y)=Aisin(ωxix+ωyiy+ψi), где Ai – амплитуда смещения при внесении ДИ, ωxi и ωyi – частоты функции деформации по каждой из осей координат изображения и ψi – фаза.

Значение амплитуды A i ограничивает максимальную величину смещения координат пикселей при внесении ДИ и определяется тем, насколько можно независимо друг от друга сместить черты лица относительно их исходных позиций так, чтобы не разрушить его общую структуру.

Частоты ω xi и ω yi определяют размеры деталей изображения, которые будут деформироваться. При малых значениях осуществляется смещение и плавная деформация изображения объекта в целом с сохранением его структурных свойств, а при их увеличении – деформируются все более мелкие его части. Исходя из этих соображений используемые в экспериментах значения ω xi и ω yi подбирались так, чтобы период функции деформации r i ( x , y ) примерно соответствовал размерам основных черт лица на изображении.

Фаза функции деформации ψ i определяет ее смещение, и для обеспечения возможности получения нескольких разных деформированных изображений на основе одного экземпляра исходной обучающей выборки ее значение генерируется случайным образом по равномерному закону на всей области определения Ω x .

В итоге реализуемый в соответствии с данной моделью алгоритм состоял в том, что для каждого из изображений исходной обучающей выборки заданное число раз с учетом описанных выше соображений генерировались параметры функции деформации, и на их основе производилось внесение ДИ с целью получить новые изображения.

На рис. 2 показаны примеры результатов внесения ДИ такого типа в изображения лиц, которые могут использоваться в качестве обучающей выборки в методе Виолы–Джонса.

Вторая модель внесения ДИ основана на часто применяемом при реализации морфинга [10, 11] подходе, заключающемся в ручной расстановке соответствий на двух совмещаемых изображениях в виде контрольных точек или контуров. Далее, на основе известных для отмеченных элементов попарных смещений или значений функции деформации в данных точках, при помощи интерполяции или некоторого другого метода находят все остальные значения функции деформации. Одним из используемых при таком подходе способов интерполяции является применение радиально-базисных функций (РБФ) [12].

Рис. 2. Примеры внесения ДИ в изображения лиц с применением гармонической функции деформации (первый столбец слева является исходным)

Реализуемый в соответствии с данной моделью алгоритм состоит в следующем. Для каждого из изображений подлежащей размножению обучающей выборки сначала производится расстановка контрольных точек ( x k , y k ), к = 1, m , где число контрольных точек m =5: по одной на глаз, кончик носа и уголки рта (рис. 3).

нямш

Рис. 3. Примеры расстановки контрольных точек на изображениях лиц

Далее рассчитываются средние значения ( x k , y k ) и их матрица ковариации, которые используются при генерации случайных положений контрольных точек для новых, искусственно получаемых данных. После этого внесение ДИ в одно из изображений исходной обучающей выборки производится следующим образом.

Генерируется случайный набор координат контрольных точек ( x k , y k ) в соответствии с полученными ранее статистическими параметрами их распределения (при генерации вместо средних значений также могут подаваться координаты самих контрольных точек размножаемого изображения). Для каждой из этих точек на основе (1) и (2) рассчитываются значения функции деформации r _i ( x_k , y_k ), i =1,2 , в данной точке так, чтобы

^f( x k ⁺ r i ⁽ x k , У к ), У к ⁺ r⁽ x k , У к )) =

= f(u( xk, Ук)) = g( xk, Ук) ’ где f(x, y) – деформируемое изображение, а g(x, y) – результат деформации, соответствующий набору случайно сгенерированных положений контрольных точек. При этом (xk + r1(xk, yk)), yk + r2(xk, yk)) – координаты контрольных точек деформируемого изображения обучающей выборки.

В данной модели конечные функции деформации r _i ( x_k , y_k ), i =1,2 , представляются в виде сумм РБФ-функций:

r⁽ x , У ) = Е m = i a ki ^exP^{( -} ( x x k) 2_G1 y y k ) ), ⁽³⁾ где о - ширина окна RBF-функций, a ki - неизвестные коэффициенты отображения. Элементам суммы соответствуют RBF-функции с центрами по координатам ( x k , y k ).

Если для x и y в координатах контрольных точек ( х_к , у_к ), к = 1, m , вместо r i ( x , y ), поочередно подставлять в (3) известные значения r i ( x k , y k ), то для каждой из функций деформации, соответствующей смещению по координатам x или y , получится по системе из m линейных уравнений (число неизвестных также равно m ):

Е m=i exp(- (xk xl)+(yk yl))an = r(xk, Ук), при к = 1, m .

В матричном виде это эквивалентно следующему уравнению:

EAi = Ri, где матрица E состоит из элементов

Е:,exp(-(xk ~xi)220(yk ~yi)2), со столбцами, пронумерованными значениями индексов l = 1, m , и строками, пронумерованными значениями к = 1,m , вектор Ai = (aii,...,aim)T содержит неизвестные коэффициенты РБФ-функций, и вектор Ri = (ri(x1, y1),…, ri(xm, ym))T – известные значения функции деформации соответствующей компоненты изображения в контрольных точках. При этом матрица E одинакова для всех ri(xk, yk), i=1,2, и не зависит от компоненты изображения.

В простейших вариантах значение о определяется экспериментально путем перебора в заданном диапазоне значений или для каждой контрольной точки и соответствующей ей РБФ-функции выставляется равным расстоянию от нее до ближайшей к ней другой контрольной точки.

Получаемые таким образом системы уравнений не всегда могут иметь стандартное решение A i = E ^–1 R i из-за плохой обусловленности матрицы уравнения или в ситуации, когда число контрольных точек меньше числа используемых для интерполяции функций. В этих случаях применяют методы регуляризации. В большинстве случаев используют расчет псевдообратной матрицы, тогда A i = E ⁺ R i , где E ⁺ – псевдообратная матрица для E , или получают решение на основе регуляризации по А.Н. Тихонову

Ai = (М+ЕтE)-1 Ет(Ri -EAiо), где I - единичная матрица размером m х m, % - параметр регуляризации, Ai0 – априорная оценка решения) [13].

На рис. 4 показаны примеры результатов внесения ДИ на основе описанного подхода.

Рис. 4. Примеры внесения ДИ в изображения лиц на основе расстановки контрольных точек и интерполяции функции деформации при помощи РБФ (первый столбец слева является исходным)

Третья модель основана на идеях определения оптического потока (ОП) в процессе изменения положений и ориентации объектов сцены в разные моменты времени или при разных условиях съемки [14,

15]. Вычисление оптического потока состоит в оценке по координатам x и y смещений содержимого сцены, которые и предлагается напрямую использовать в качестве функций деформации r _i ( x , y ), i =1,2 . Существует множество механизмов определения оптического потока [15 – 17]. Каждый из них ограничен своей областью применимости из-за заложенных в него допущений, на основе которых и производится его расчет. Выбранный для данной модели метод Фарне-бака [17] работает следующим образом. Оба изображения (предварительно сглаженные) представляются в виде квадратичных полиномов вида:

f(x) = xт Ax + bx + c , где x = (x, y)T, и A, b, с – параметры полинома, значения которых во время его построения вычисляются в соответствии с критерием наименьших квадратов: A – симметричная матрица, b – вектор, с – скаляр. При расчете оптического потока между кадрами f1(x) и f2(x) ищется смещение d, удовлетворяющее уравнениям:

f₂ ( x ) = f 1 ( x - d ) = ( x - d ) ^т A 1 ( x - d ) +

+ b 1 ( x - d ) + c 1 = x ^т A 2 x + b ₂ x + c 2 .

Для повышения точности используемого приближения построение полинома при этом производится не для всего изображения, а для некоей его области, и, таким образом, все коэффициенты A , b , c и смещение d становятся зависимыми от координат x =( x , y )^T: A ( x ), b ( x ), c ( x ) и d ( x ). Особенностью метода Фарнебака является возможность вычисления потоков большой величины всего для двух соседних по времени кадров за счет итерационного характера расчета d ( x ) в разных масштабах от меньшего к большему с постепенным уточнением получающихся значений [17].

Из-за специфики предметной области – обработка изображений лиц, разницу между которыми нельзя увязать к смещению положений их пикселей – перед процедурой поиска оптического потока требуется провести дополнительное преобразование. Им является операция наложения фильтра энтропии [18], который для каждой координаты изображения и ее окрестности из n пикселей вычисляется следующим образом. Рассчитываются вероятности p_t, i = 1, n , появления каждого значения интенсивности пикселя в данной области, и на их основе – энтропия ее центрального пикселя:

^{e( x} , У ) = ^- S n-P. log Pi , 1

где e( x , y ) – результат наложения фильтра, который и используется для поиска оптического потока.

Таким образом, изображения лиц заменяются образами, отражающими их основную структуру. В них мелкие черты лица соответствуют высоким значениям энтропии, а фон и кожа лба и щек – более низким (рис. 5).

В итоге размножение изображений обучающей выборки осуществлялось следующим образом. На каждое из них производилось наложение фильтра энтропии и вычисление e(x, y). После чего рассчитыва- лись выборочные параметры энтропии: среднее и матрица ковариации.

Рис. 5. Примеры наложения фильтра энтропии на изображения лиц

Далее, при размножении каждого изображения исходной обучающей выборки производилась генерация случайных значений энтропии e g ( x , y ) и расчет функции деформации r _i ( x , y ), i =1,2 , путем вычисления оптического потока между сгенерированным значением энтропии и энтропией размножаемого изображения. Полученный результат r _i ( x , y ), i =1,2 , и использовался при внесении ДИ в качестве функции деформации. На рис. 6 показаны примеры работы алгоритма, основанного на данной модели.

Рис. 6. Примеры внесения ДИ в изображения лиц на основе наложения фильтра энтропии и расчета ОП (первый столбец слева является исходным)

3.    Результаты экспериментальных исследований

Для оценки влияния искусственного размножения элементов обучающей выборки на качество детектирования были проведены эксперименты по обучению детекторов лиц по методу Виолы–Джонса с последующими замерами точности их работы. Обучение было осуществлено с использованием пяти вариантов формирования обучающих выборок:

– оригинальная, содержащая 4916 изображений лиц, собранных и подготовленных вручную авторами метода Виолы–Джонса [4, 5];

– усеченная, содержащая 492 изображения лиц из числа изображений оригинальной выборки;

– три искусственно размноженные выборки, содержащие по 4916 изображений лиц, из которых 492 изображения принадлежали усеченному набору изображений, а остальные (по 9 на каждое из исходных) сгенерированы искусственно, путем внесения ДИ на основе каждой из описанных выше моделей.

Оценка качества детектирования производилось следующим образом. Для каждого детектора модифицировался порог его реагирования, и в соответ- ствии с полученными откликами были построены зависимости относительной частоты правильно найденных лиц от числа ложных срабатываний (рис. 7). В качестве изображений для тестирования был использован специальный набор изображений из выборки CMU+ MIT [19], часто применяемый для сравнения работы детекторов фронтальных лиц и со-

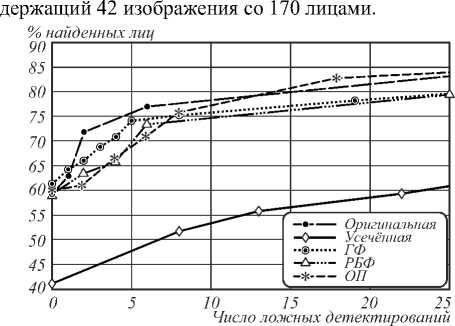
Рис. 7. Зависимости для относительной частоты правильно найденных лиц от числа ложных срабатываний, полученные при обучении по оригинальной и усеченной выборкам, а также с использованием трех рассмотренных моделей размножения обучающих данных

В табл. 1 представлены типичные результаты, полученные для каждого из детекторов при схожем числе ложных срабатываний.

Табл. 1. Относительные частоты правильно найденных лиц при схожем числе ложных срабатываний, полученные при обучении по оригинальной и усеченной выборкам, а также с использованием трех рассмотренных моделей размножения обучающих данных

	Оригинальная	Усеченная	ГФ	РБФ	ОП
Процент найденных лиц	83,53	59,41	78,23	79,41	82,94
Число ложных срабатываний	26	22	19	25	18

Анализ данных табл. 1 и полученных зависимостей (рис. 7) показывает, что при схожем числе ложных срабатываний детектор, обученный с использованием усеченной выборки, стабильно выдает результаты хуже оригинального примерно на 20 %. В то же время детекторы, основанные на трех рассмотренных выше моделях размножения элементов обучающих данных путем внесения в них ДИ, дают сравнимый с оригиналом результат с отклонением от него по большей части в пределах 5 %. Таким образом, показано значительное увеличение точности их работы при сравнении с классификатором, основанным на усеченной обучающей выборке (которая и была использована для размножения).

Заключение

Полученные результаты позволяют говорить о применимости данного подхода к задачам построения детекторов обнаружения объектов, имеющих ярко выраженные структурные характеристики, для сокращения затрат на поиск и подготовку обучающих данных, а также в условиях невозможности сбора достаточного для начала процесса обучения количества элементов тренировочной выборки.