Модели и численное решение некоторых динамических контактных задач наномеханики

This work presents generalization of classical Tomlinson’s model of nanostructures contact taking into account forces of inertia and forces of viscous resistance is offered. Generalization consists in the account of forces of interaction on distance of all elements of nanosystems at preservation of the basic idea of Tomlinsona – about problem reduction to research of interaction of boundary layers of atoms. For the decision of one-dimensional problems the standard algorithm of Runge – Kutta is used. Efforts of contact interaction are found. Influence of the relation of the periods of cooperating boundary chains is studied. The three-dimensional problem about a finding of forces of interaction of pair кластеров the cubic form is solved

Задачи наномеханики заключаются, как известно, в нахождении усилий взаимодействия между частицами наносистем и взаимных перемещений наночастиц, составляющих наносистему; для краткости наночастицы обычно называют атомами. В соответствии с принятыми определениями к наносистемам относят объекты, характерные размеры которых лежат в диапазоне от 1 до 100 нанометров (нм). Сформулированную задачу наномеханики можно ставить как квазистатическую, пренебрегая силами инерции, или же как динамическую, учитывая силы инерции. В настоящей работе исследуются некоторые задачи нанотрибологии, представляющие собой частный, но очень важный для приложений класс задач наномеханики. Объектом исследования в трибологических задачах является процесс контактного взаимодействия двух наносистем при задании их относительного движения. Квазистатиче-ские задачи были изучены в предыдущих работах. В настоящей работе рассматриваются одномерные динамические задачи нанотрибологии; решена одна трехмерная задача.

1.    Одномерные задачи

Впервые одномерная задача нанотрибологии была рассмотрена Томлинсоном в 1928 г. [1]. Им была предложена модель контактного взаимодействия двух кристаллических тел, представленная на рис. 1. В модели Томлинсона предполагается, что нижний кристалл движется относительно верхнего параллельно общей прямолинейной границе, принятой за ось Ox .

Основные гипотезы Томлинсона таковы:

Рис. 1. Переход от взаимодействия кристаллических тел (верхняя часть) к взаимодействию гранич-слоев (внизу)

• 1)    Силовое взаимодействие двух кристаллических тел может быть аппроксимировано взаимодействием поверхностных слоев атомов, как показано в нижней части рис. 1. Атомы в этих слоях могут двигаться только вдоль некоторой прямой, принятой за ось Ox.

• 2)    Нижний слой атомов (цепочка) является абсолютно жестким, верхний слой - деформируемым. Их взаимодействие является парным силовым взаимодействием на расстоянии и имеет толь-

• ко одну компоненту, параллельную оси Ox. Эта компонента аппроксимиру

ется синусоидой.

• 3)    Каждый атом верхней цепочки движется независимо - без взаимодействия с другими атомами этой же цепочки. Силовая реакция атомов верхнего тела, не принадлежащих граничной цепочке, линейно зависит от перемещения данного атома в деформируемой цепочке. Из гипотез Томлинсона

вытекает следующее уравнение движения:

du 7    . Г -   ^2П /0      . Т Т

, x i = 1Г е ,

m—^ = -ku + f sin — x-u + U dt2           i 1 aV 1      1 c где ui - перемещение i -го атома; m - масса атома; k - коэффициент жесткости основания, re - период (равновесное расстояние) между атомами деформируемой цепочки, а - заданное отношение периода а жесткой цепочки к периоду re деформируемой, а = ren, n; Uc - заданное перемещение жесткой цепочки. Очевидно, что форма уравнений равновесия одна и та же для всех атомов, различны лишь силовые воздействия на них. Для сопоставления решений, найденных для модели Томлинсона, с решениями для других моделей, в которых учитывается взаимодействие атомов в цепочке, уравнение (1) решается для значений индекса i = 0,1, 2,..., N.

В работе [2] была предложена модель, в которой учитывалось взаимодействие соседних атомов по линейному закону. Исторический обзор и описание последних результатов в решении проблемы можно найти в [3]. Решения квазистатических задач опубликованы в [4 - 6].

Предлагаемое обобщение модели Томлинсона заключается в следующем. Рассматривается конечная цепочка, атомы которой занумерованы целыми числами i, i = 0,1, 2,..., N. Атом «0» закреплен, перемещения остальных атомов неизвестны и подлежат определению. Начальное расстояние между соседними атомами равно re, текущее положение атома i равно iri + ui. На цепочку воздействуют внешние силы Fex, порождаемые подвижной жесткой цепочкой. Кроме того, на состояние равновесия влияют внутренние силы в цепочке: с левой стороны на атом действуют силы FiL, с правой - силы FiR. Сила Fext имеет две компоненты - определение дано ниже; вторая компонента - проекция на вертикаль - интерпретируется как сила адгезии. Атомы жесткой цепочки занумерованы целыми числами j, j = 0,1, 2,..., NA. Расчетная схема показана на рис. 2.

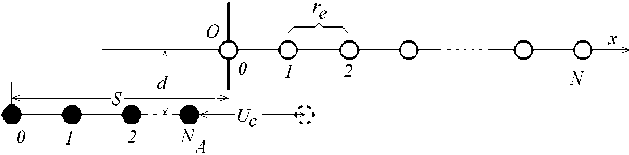
Рис. 2. Обобщенная модель

Расстояние между жесткой и деформируемой цепочками обозначено через d , S - начальное положение атома с номером j = 0, U c - текущее значение перемещения жесткой цепочки. Уравнение движения для обобщенной модели имеет вид:

d 2 U й/-\— * R * L , *ext d^U m —у = Т ( и ) = F - F + F -у— ,             (2) dt 2                                 dt

где

F R = 2 D a £ { exp [ -a ( xp - x i - r e + u p - и ) ] - p = i + i                                                                (3) -    exp [ - 2 « ( X p - x i - r e ) + u p - u i ) ] } , F iL = 2 D a £ { exp F -a ( xi - x p - r e + U - u p ) ] - p = 0                                                           (4) -    exp [ - 2 « ( x i -- x p - r e ) + M i- - U p ) ] } . 2 A { exp [ -a ( r il - r e ) ] - exp [ - 2 a ( r il - r e ) ] } cos P il , F * ext = 2 D a l = 0                                                            (5) E { exp [ -a ( r il - r e ) ] - exp [ - 2 a ( r il - r e ) ] } sin в il . <    l = 0                                                              ;

где D , a , r e - константы потенциала Морса, зависящие от материала, эти константы имеются в справочниках; r il - расстояние между атомами с номерами i , l , i соответствуеещее атому деформируемой цепочки, l - атому подвижной жесткой цепочки; в il - угол наклона радиус-вектора r il = r - ^:r_l к оси Ox ; у - коэффициент вязкого сопротивления. К уравнениям (1)-(2) необходимо добавить начальные условия, а также задать внешние воздействия (помимо усилий F ext в (2)), например, перемещения u_N 1 + _N 2 или силы Fj L 1 _{+ N} 2 .

2.    Примеры численных решений

Для решения одномерных задач был использован метод Рунге - Кутта 4-го порядка. Находились перемещения, локальные и полные силы трения и адгезии. Локальные силы трения F fr\_oc определялись как силы в проекции на ось Ox , действующие на отдельный атом; полная сила трения F f _r tot равна сумме локальных. Полная сила трения для модели Томлинсона не вычисляется, так как здесь уравнения описывают поведение отдельных атомов без их взаимодействия друг с другом. Локальная сила адгезии F ad ) _loc определяется так же, как и локальная сила трения, и не может быть определена для класс-сической модели Томлинсона. Полная сила адгезии F_ad tot равна сумме локальных.

• Пример 1: некоторые результаты для обобщенной модели.

Уравнения обобщенной модели решаются для двух наборов входных данных. Для первого набора разрушения цепочки нет, для второго на некотором шаге нагружения цепочка разрывается на две равные части.

Для первого набора входных данных:

N = 20, N a = 10, N _toad = 500, 5 = 0, U_ = 10 r , d = 2, a = b , где U _max - максимальное значение перемещения жесткой цепочки, N load -количество шагов нагружения (точек разбиения интервала [ 0, U _max ] ). Изучены два варианта для у = 0 и у= 0,5.

Второй набор входных данных:

N = 20, N a = 10, N ^ = 500, 5 = 0, U max = 10 r_e , d = 1, a = b также был реализован для у= 0 и у = 0,5.

Найденная зависимость перемещений от времени показана на рис. 3 для 10-го атома при у = 0; сплошная кривая соответствует первому набору входных данных, точечная кривая иллюстрирует эффект разрушения. Разрушение начинается в момент начала линейного роста перемещения U ₁₀ - рост по линейному закону означает, что часть деформируемой цепочки, с 10-го по 20-й атом, движется вместе с жесткой цепочкой.

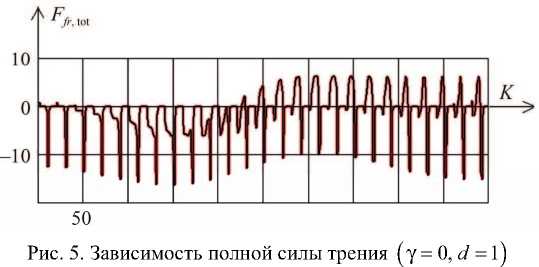
Зависимость полной силы трения F fr tot от времени показана на рис. 4, 5.

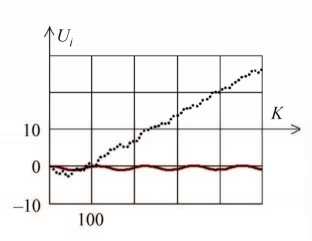
Рис. 3. Зависимость перемещений 10-го атома от времени

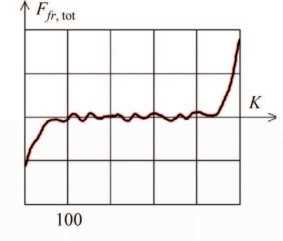
Рис. 4. Зависимость полной силы трения ( у = 0, d = 2 )

Пример 2: некоторые результаты для динамической модели Томлинсона. Напомним, что в данной модели количество атомов бесконечно. Следовательно, графические представления результатов для разных атомов различаются только переносом вдоль временной оси. Кривые на рис. 6 иллюстрируют зависимость сил трения F to loc = F to tom от времени (номер шага нагружения обозначен через K = 1, ...,100). В расчетах использована замена f 1 = kX /(2 п ), где X - параметр, регулирующий устойчивость состояния

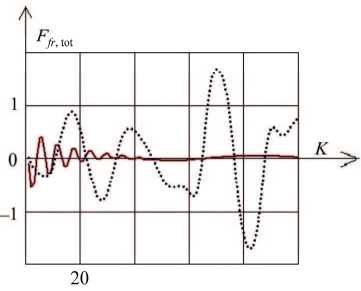
Рис. 6. Сплошная кривая соответствует значению у= 0,5, для точечной у= 0

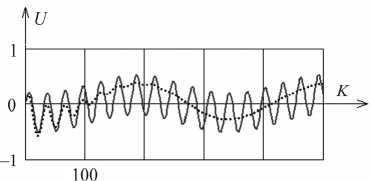
Рис. 7. Сплошная кривая соответствует значениям у = 0, X = 1/ r e ; для точечной у= 0,5, Х = 2

равновесия в квазистатике, введенный в работе [1]; приведенные результаты соответствуют значению X = п .

Кривые на рис. 7 иллюстрируют зависимость перемещений от изменения отношения п периодов цепочек.

3.    Трехмерные задачи динамики

Для решения трехмерных задач был использован хорошо известный метод Верле [7]. Рассмотренная контактная задача показана на рис. 8. Речь идет об определении усилий контактного взаимодействия двух наноструктур, состоящих из дискретных частиц (атомов), заполняющих области в форме куба. Эти области называют кластерами. Расположение атомов в нижнем кластере воспроизводит кристаллическую структуру алюминия, в верхнем -меди. Предполагается, что нижний кластер является абсолютно жестким и состоит из 6912 атомов, взаимодействующих с деформируемым кластером из атомов меди по закону Морса. Кла-

Рис. 8. Контактное взаимодействие двух кластеров

стер меди содержит 256 атомов меди, что позволяет решить задачу с использованием обычного персонального компьютера. Учитывается влияние веса атомов верхнего кластера. Температура принята равной 300 °K.

Построение геометрической модели обоих кластеров производится так, как это описано в [7]. Для нахождения полной силы трения использована расчетная схема, показанная на рис. 9. Верхний кластер соединен с верхним подвижным приводом при помощи линейно упругой пружины. Силы взаимодействия атомов подчиняются закону Морса. Уравнения движения атома в исследуемой системе представляют собой уравнения классической механики материальной точки. Начальные условия формируются при помощи датчика случайных чисел так, как это сделано в [7], - этот прием позволяет ввести в рассмотрение температуру.

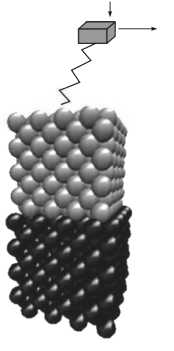
Рис. 9. Расчетная схема

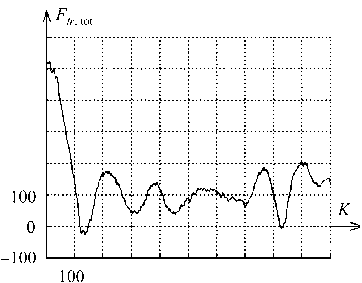
Рис. 10. Зависимость F fr tot от номера временного шага K

Полная сила трения F fr ,tot , найденная при решении задачи, показана на рис. 10. Характер ее поведения можно трактовать как проявление эффекта «stick-slip». Этот эффект заключается в переходе от режима, при котором верхний атом движется с нарастанием силы в пружине (режим «slip - сцепление») к новому состоянию системы путем резкого уменьшении полной силы взаимодействия (режим «stick - проскальзывание»).

Этот эффект проявляется в контактных задачах с учетом трения на макромасштабе. В классических контактных задачах установлено, что данный эффект в динамике проявляется, в частности, в появлении колебаний контактирующих тел с частотами, иногда лежащими в диапазоне частот слышимого звука, что имеет место в смычковых музыкальных инструментах.

Заключение

Полученные результаты позволяют сделать следующие выводы:

• 1)    Предложенное обобщение классической модели Томлинсона позволяет изучать поведение конечного числа атомов и решать контактные задачи наномеханики в уточненной постановке - без использования синусоидальной

аппроксимации сил дальнодействия, находить - в отличие от теории Томлинсона - силы адгезии, а также моделировать эффект разрушения.

• 2)    Предложенная модель учета сил дальнодействия между частицами наносистемы представляет собой реализацию первого этапа метода многих масштабов в решении контактных задач. Выявленные эффекты могут быть использованы при построении моделей контактного взаимодействия на мезоуровне.

Работа выполнена при частичной финансовой поддержке грантов РФФИ №08-01-00349, 10-08-00425 и проекта 2.1.1/5873 аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы».